Domain based classification

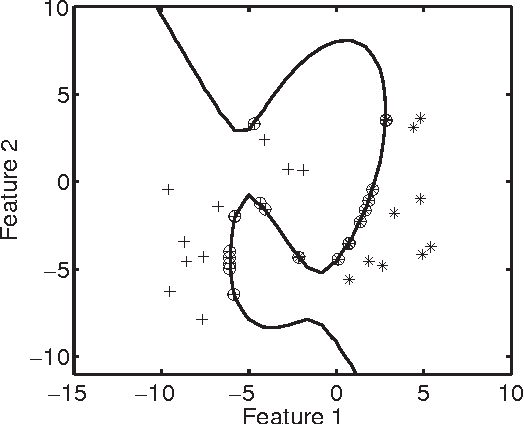
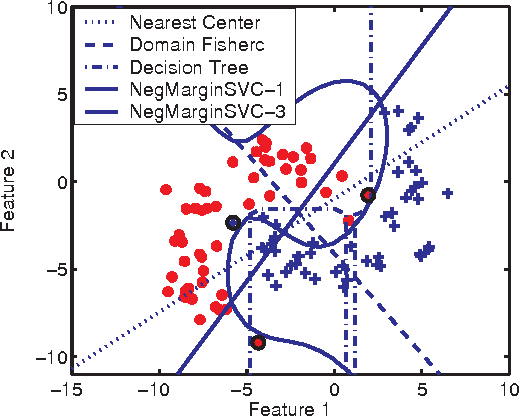
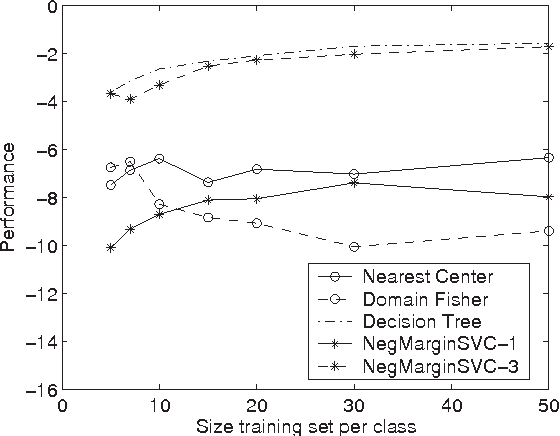
The majority of traditional classification ru les minimizing the expected probability of error (0-1 loss) are inappropriate if the class probability distributions are ill-defined or impossible to estimate. We argue that in such cases class domains should be used instead of class distributions or densities to construct a reliable decision function. Proposals are presented for some evaluation criteria and classifier learning schemes, illustrated by an example.

Scalable Prototype Selection by Genetic Algorithms and Hashing

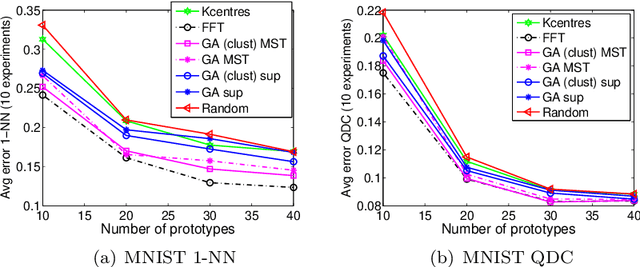
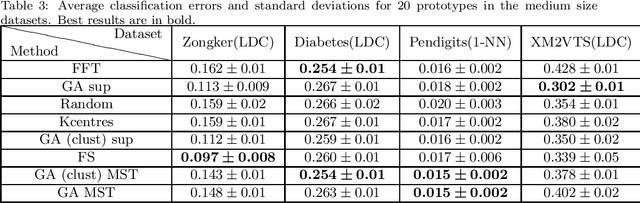
Classification in the dissimilarity space has become a very active research area since it provides a possibility to learn from data given in the form of pairwise non-metric dissimilarities, which otherwise would be difficult to cope with. The selection of prototypes is a key step for the further creation of the space. However, despite previous efforts to find good prototypes, how to select the best representation set remains an open issue. In this paper we proposed scalable methods to select the set of prototypes out of very large datasets. The methods are based on genetic algorithms, dissimilarity-based hashing, and two different unsupervised and supervised scalable criteria. The unsupervised criterion is based on the Minimum Spanning Tree of the graph created by the prototypes as nodes and the dissimilarities as edges. The supervised criterion is based on counting matching labels of objects and their closest prototypes. The suitability of these type of algorithms is analyzed for the specific case of dissimilarity representations. The experimental results showed that the methods select good prototypes taking advantage of the large datasets, and they do so at low runtimes.

Fast kNN mode seeking clustering applied to active learning

A significantly faster algorithm is presented for the original kNN mode seeking procedure. It has the advantages over the well-known mean shift algorithm that it is feasible in high-dimensional vector spaces and results in uniquely, well defined modes. Moreover, without any additional computational effort it may yield a multi-scale hierarchy of clusterings. The time complexity is just O(n^1.5). resulting computing times range from seconds for 10^4 objects to minutes for 10^5 objects and to less than an hour for 10^6 objects. The space complexity is just O(n). The procedure is well suited for finding large sets of small clusters and is thereby a candidate to analyze thousands of clusters in millions of objects. The kNN mode seeking procedure can be used for active learning by assigning the clusters to the class of the modal objects of the clusters. Its feasibility is shown by some examples with up to 1.5 million handwritten digits. The obtained classification results based on the clusterings are compared with those obtained by the nearest neighbor rule and the support vector classifier based on the same labeled objects for training. It can be concluded that using the clustering structure for classification can be significantly better than using the trained classifiers. A drawback of using the clustering for classification, however, is that no classifier is obtained that may be used for out-of-sample objects.

Zero-error dissimilarity based classifiers

We consider general non-Euclidean distance measures between real world objects that need to be classified. It is assumed that objects are represented by distances to other objects only. Conditions for zero-error dissimilarity based classifiers are derived. Additional conditions are given under which the zero-error decision boundary is a continues function of the distances to a finite set of training samples. These conditions affect the objects as well as the distance measure used. It is argued that they can be met in practice.

A Two-Stage Combined Classifier in Scale Space Texture Classification

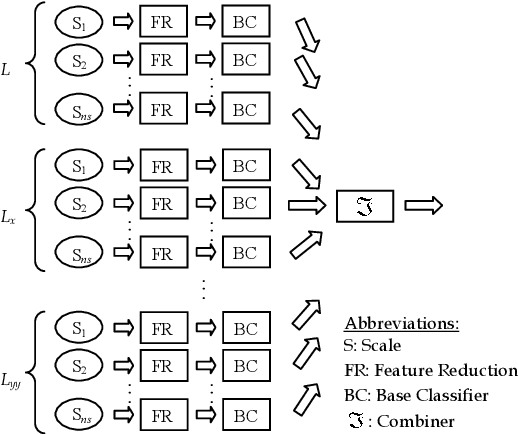
Textures often show multiscale properties and hence multiscale techniques are considered useful for texture analysis. Scale-space theory as a biologically motivated approach may be used to construct multiscale textures. In this paper various ways are studied to combine features on different scales for texture classification of small image patches. We use the N-jet of derivatives up to the second order at different scales to generate distinct pattern representations (DPR) of feature subsets. Each feature subset in the DPR is given to a base classifier (BC) of a two-stage combined classifier. The decisions made by these BCs are combined in two stages over scales and derivatives. Various combining systems and their significances and differences are discussed. The learning curves are used to evaluate the performances. We found for small sample sizes combining classifiers performs significantly better than combining feature spaces (CFS). It is also shown that combining classifiers performs better than the support vector machine on CFS in multiscale texture classification.