Domain based classification

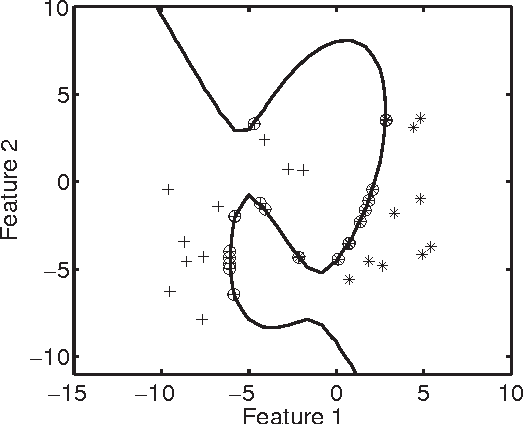
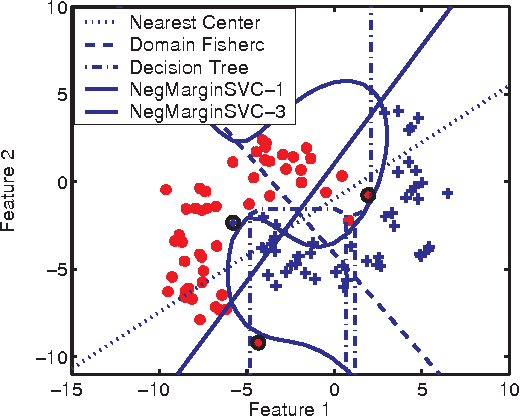
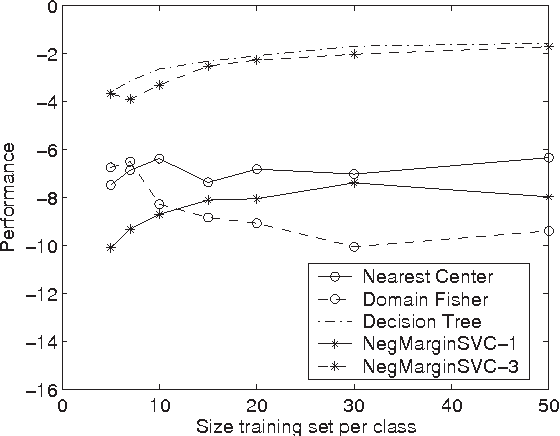
The majority of traditional classification ru les minimizing the expected probability of error (0-1 loss) are inappropriate if the class probability distributions are ill-defined or impossible to estimate. We argue that in such cases class domains should be used instead of class distributions or densities to construct a reliable decision function. Proposals are presented for some evaluation criteria and classifier learning schemes, illustrated by an example.

Zero-error dissimilarity based classifiers

We consider general non-Euclidean distance measures between real world objects that need to be classified. It is assumed that objects are represented by distances to other objects only. Conditions for zero-error dissimilarity based classifiers are derived. Additional conditions are given under which the zero-error decision boundary is a continues function of the distances to a finite set of training samples. These conditions affect the objects as well as the distance measure used. It is argued that they can be met in practice.