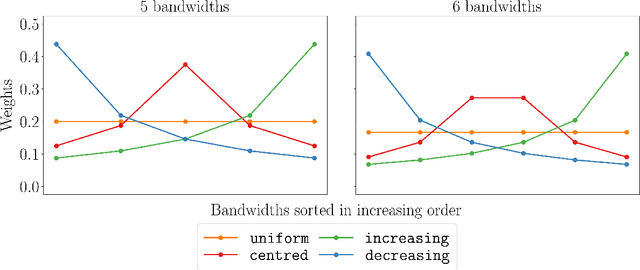
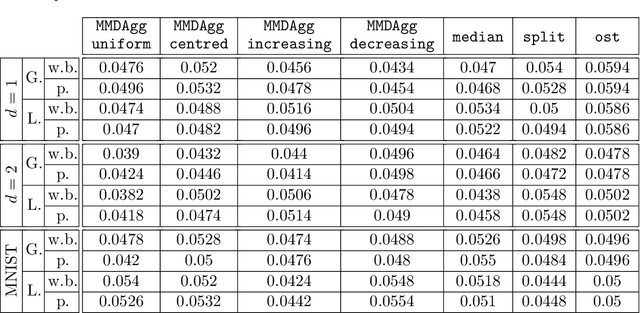
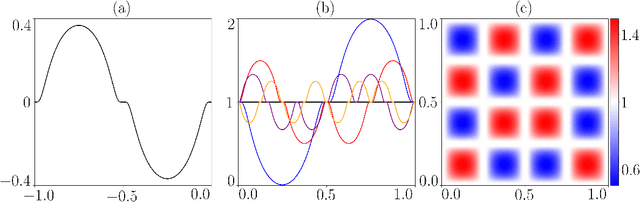
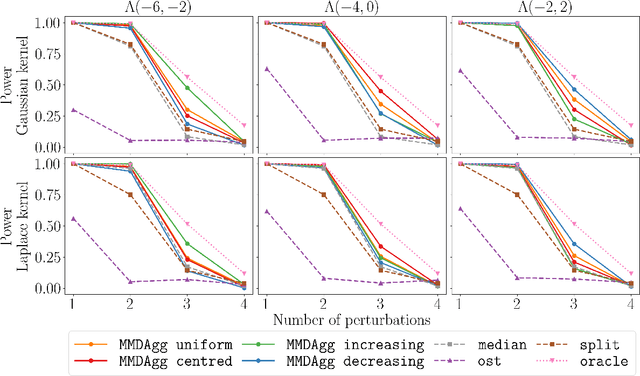
MMD Aggregated Two-Sample Test

We propose a novel nonparametric two-sample test based on the Maximum Mean Discrepancy (MMD), which is constructed by aggregating tests with different kernel bandwidths. This aggregation procedure, called MMDAgg, ensures that test power is maximised over the collection of kernels used, without requiring held-out data for kernel selection (which results in a loss of test power), or arbitrary kernel choices such as the median heuristic. We work in the non-asymptotic framework, and prove that our aggregated test is minimax adaptive over Sobolev balls. Our guarantees are not restricted to a specific kernel, but hold for any product of one-dimensional translation invariant characteristic kernels which are absolutely and square integrable. Moreover, our results apply for popular numerical procedures to determine the test threshold, namely permutations and the wild bootstrap. Through numerical experiments on both synthetic and real-world datasets, we demonstrate that MMDAgg outperforms alternative state-of-the-art approaches to MMD kernel adaptation for two-sample testing.

Minimax optimal goodness-of-fit testing for densities under a local differential privacy constraint

Finding anonymization mechanisms to protect personal data is at the heart of machine learning research. Here we consider the consequences of local differential privacy constraints on goodness-of-fit testing, i.e. the statistical problem assessing whether sample points are generated from a fixed density $f_0$, or not. The observations are hidden and replaced by a stochastic transformation satisfying the local differential privacy constraint. In this setting, we propose a new testing procedure which is based on an estimation of the quadratic distance between the density $f$ of the unobserved sample and $f_0$. We establish minimax separation rates for our test over Besov balls. We also provide a lower bound, proving the optimality of our result. To the best of our knowledge, we provide the first minimax optimal test and associated private transformation under a local differential privacy constraint, quantifying the price to pay for data privacy.

Wikistat 2.0: Educational Resources for Artificial Intelligence

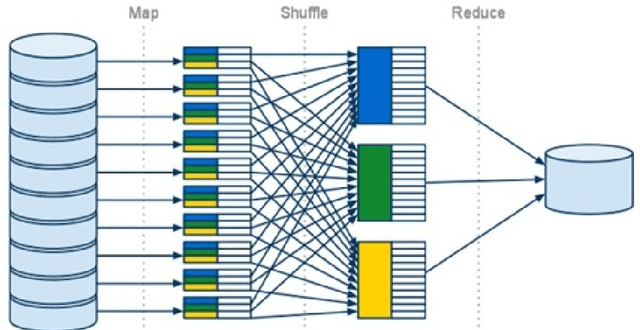
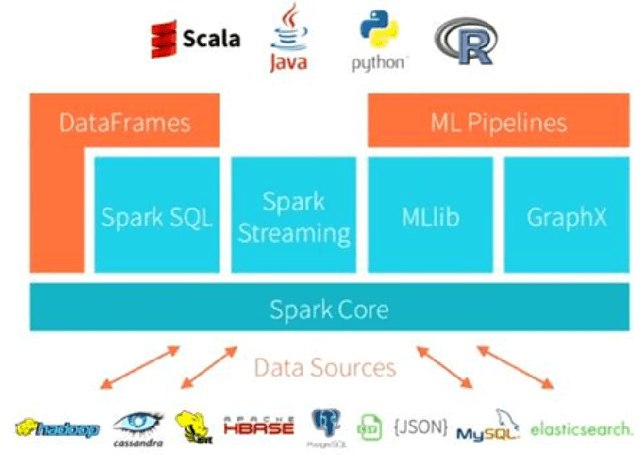
Big data, data science, deep learning, artificial intelligence are the key words of intense hype related with a job market in full evolution, that impose to adapt the contents of our university professional trainings. Which artificial intelligence is mostly concerned by the job offers? Which methodologies and technologies should be favored in the training programs? Which objectives, tools and educational resources do we needed to put in place to meet these pressing needs? We answer these questions in describing the contents and operational resources in the Data Science orientation of the specialty Applied Mathematics at INSA Toulouse. We focus on basic mathematics training (Optimization, Probability, Statistics), associated with the practical implementation of the most performing statistical learning algorithms, with the most appropriate technologies and on real examples. Considering the huge volatility of the technologies, it is imperative to train students in seft-training, this will be their technological watch tool when they will be in professional activity. This explains the structuring of the educational site github.com/wikistat into a set of tutorials. Finally, to motivate the thorough practice of these tutorials, a serious game is organized each year in the form of a prediction contest between students of Master degrees in Applied Mathematics for IA.

Multiple testing for outlier detection in functional data

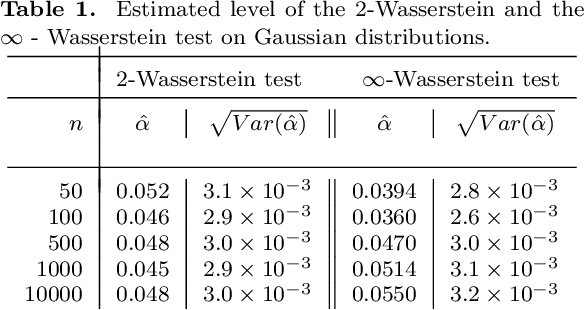
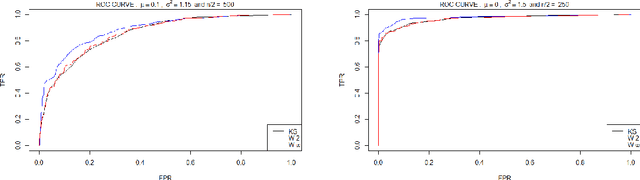
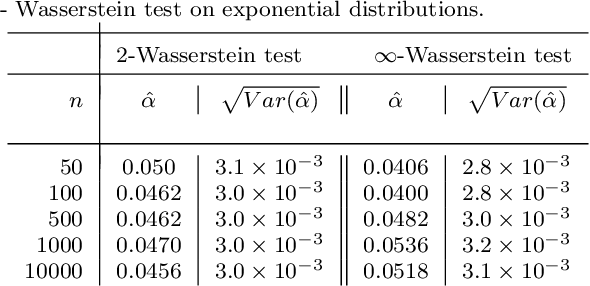
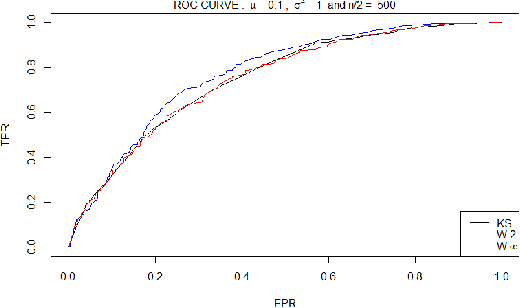
We propose a novel procedure for outlier detection in functional data, in a semi-supervised framework. As the data is functional, we consider the coefficients obtained after projecting the observations onto orthonormal bases (wavelet, PCA). A multiple testing procedure based on the two-sample test is defined in order to highlight the levels of the coefficients on which the outliers appear as significantly different to the normal data. The selected coefficients are then called features for the outlier detection, on which we compute the Local Outlier Factor to highlight the outliers. This procedure to select the features is applied on simulated data that mimic the behaviour of space telemetries, and compared with existing dimension reduction techniques.