Does Weather Matter? Causal Analysis of TV Logs

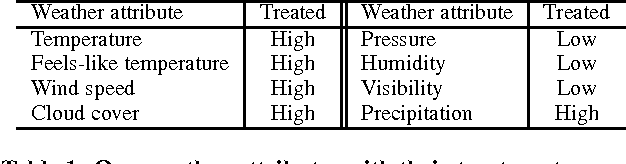
Weather affects our mood and behaviors, and many aspects of our life. When it is sunny, most people become happier; but when it rains, some people get depressed. Despite this evidence and the abundance of data, weather has mostly been overlooked in the machine learning and data science research. This work presents a causal analysis of how weather affects TV watching patterns. We show that some weather attributes, such as pressure and precipitation, cause major changes in TV watching patterns. To the best of our knowledge, this is the first large-scale causal study of the impact of weather on TV watching patterns.

Efficient Learning in Large-Scale Combinatorial Semi-Bandits

A stochastic combinatorial semi-bandit is an online learning problem where at each step a learning agent chooses a subset of ground items subject to combinatorial constraints, and then observes stochastic weights of these items and receives their sum as a payoff. In this paper, we consider efficient learning in large-scale combinatorial semi-bandits with linear generalization, and as a solution, propose two learning algorithms called Combinatorial Linear Thompson Sampling (CombLinTS) and Combinatorial Linear UCB (CombLinUCB). Both algorithms are computationally efficient as long as the offline version of the combinatorial problem can be solved efficiently. We establish that CombLinTS and CombLinUCB are also provably statistically efficient under reasonable assumptions, by developing regret bounds that are independent of the problem scale (number of items) and sublinear in time. We also evaluate CombLinTS on a variety of problems with thousands of items. Our experiment results demonstrate that CombLinTS is scalable, robust to the choice of algorithm parameters, and significantly outperforms the best of our baselines.

Combinatorial Cascading Bandits

We propose combinatorial cascading bandits, a class of partial monitoring problems where at each step a learning agent chooses a tuple of ground items subject to constraints and receives a reward if and only if the weights of all chosen items are one. The weights of the items are binary, stochastic, and drawn independently of each other. The agent observes the index of the first chosen item whose weight is zero. This observation model arises in network routing, for instance, where the learning agent may only observe the first link in the routing path which is down, and blocks the path. We propose a UCB-like algorithm for solving our problems, CombCascade; and prove gap-dependent and gap-free upper bounds on its $n$-step regret. Our proofs build on recent work in stochastic combinatorial semi-bandits but also address two novel challenges of our setting, a non-linear reward function and partial observability. We evaluate CombCascade on two real-world problems and show that it performs well even when our modeling assumptions are violated. We also demonstrate that our setting requires a new learning algorithm.

Cascading Bandits: Learning to Rank in the Cascade Model

A search engine usually outputs a list of $K$ web pages. The user examines this list, from the first web page to the last, and chooses the first attractive page. This model of user behavior is known as the cascade model. In this paper, we propose cascading bandits, a learning variant of the cascade model where the objective is to identify $K$ most attractive items. We formulate our problem as a stochastic combinatorial partial monitoring problem. We propose two algorithms for solving it, CascadeUCB1 and CascadeKL-UCB. We also prove gap-dependent upper bounds on the regret of these algorithms and derive a lower bound on the regret in cascading bandits. The lower bound matches the upper bound of CascadeKL-UCB up to a logarithmic factor. We experiment with our algorithms on several problems. The algorithms perform surprisingly well even when our modeling assumptions are violated.

Tight Regret Bounds for Stochastic Combinatorial Semi-Bandits

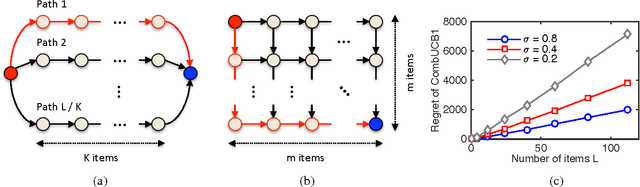
A stochastic combinatorial semi-bandit is an online learning problem where at each step a learning agent chooses a subset of ground items subject to constraints, and then observes stochastic weights of these items and receives their sum as a payoff. In this paper, we close the problem of computationally and sample efficient learning in stochastic combinatorial semi-bandits. In particular, we analyze a UCB-like algorithm for solving the problem, which is known to be computationally efficient; and prove $O(K L (1 / \Delta) \log n)$ and $O(\sqrt{K L n \log n})$ upper bounds on its $n$-step regret, where $L$ is the number of ground items, $K$ is the maximum number of chosen items, and $\Delta$ is the gap between the expected returns of the optimal and best suboptimal solutions. The gap-dependent bound is tight up to a constant factor and the gap-free bound is tight up to a polylogarithmic factor.

Learning to Act Greedily: Polymatroid Semi-Bandits

Many important optimization problems, such as the minimum spanning tree and minimum-cost flow, can be solved optimally by a greedy method. In this work, we study a learning variant of these problems, where the model of the problem is unknown and has to be learned by interacting repeatedly with the environment in the bandit setting. We formalize our learning problem quite generally, as learning how to maximize an unknown modular function on a known polymatroid. We propose a computationally efficient algorithm for solving our problem and bound its expected cumulative regret. Our gap-dependent upper bound is tight up to a constant and our gap-free upper bound is tight up to polylogarithmic factors. Finally, we evaluate our method on three problems and demonstrate that it is practical.

DUM: Diversity-Weighted Utility Maximization for Recommendations

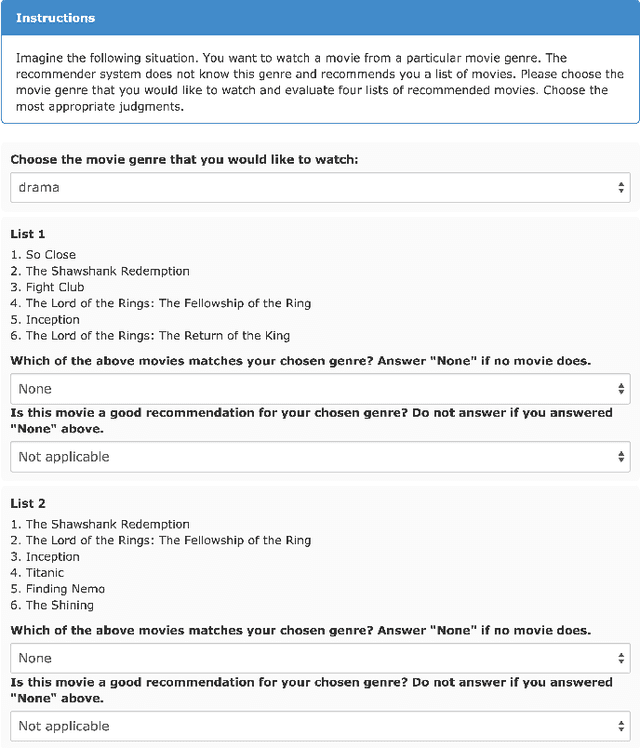
The need for diversification of recommendation lists manifests in a number of recommender systems use cases. However, an increase in diversity may undermine the utility of the recommendations, as relevant items in the list may be replaced by more diverse ones. In this work we propose a novel method for maximizing the utility of the recommended items subject to the diversity of user's tastes, and show that an optimal solution to this problem can be found greedily. We evaluate the proposed method in two online user studies as well as in an offline analysis incorporating a number of evaluation metrics. The results of evaluations show the superiority of our method over a number of baselines.

Matroid Bandits: Fast Combinatorial Optimization with Learning

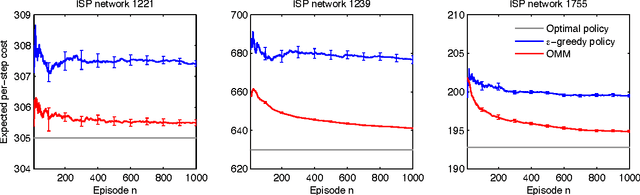
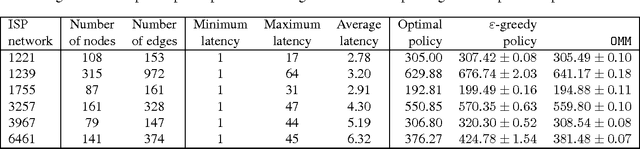
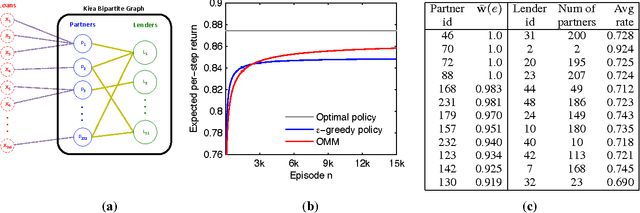
A matroid is a notion of independence in combinatorial optimization which is closely related to computational efficiency. In particular, it is well known that the maximum of a constrained modular function can be found greedily if and only if the constraints are associated with a matroid. In this paper, we bring together the ideas of bandits and matroids, and propose a new class of combinatorial bandits, matroid bandits. The objective in these problems is to learn how to maximize a modular function on a matroid. This function is stochastic and initially unknown. We propose a practical algorithm for solving our problem, Optimistic Matroid Maximization (OMM); and prove two upper bounds, gap-dependent and gap-free, on its regret. Both bounds are sublinear in time and at most linear in all other quantities of interest. The gap-dependent upper bound is tight and we prove a matching lower bound on a partition matroid bandit. Finally, we evaluate our method on three real-world problems and show that it is practical.