Sharp Convergence Rates of Empirical Unbalanced Optimal Transport for Spatio-Temporal Point Processes

We statistically analyze empirical plug-in estimators for unbalanced optimal transport (UOT) formalisms, focusing on the Kantorovich-Rubinstein distance, between general intensity measures based on observations from spatio-temporal point processes. Specifically, we model the observations by two weakly time-stationary point processes with spatial intensity measures $\mu$ and $\nu$ over the expanding window $(0,t]$ as $t$ increases to infinity, and establish sharp convergence rates of the empirical UOT in terms of the intrinsic dimensions of the measures. We assume a sub-quadratic temporal growth condition of the variance of the process, which allows for a wide range of temporal dependencies. As the growth approaches quadratic, the convergence rate becomes slower. This variance assumption is related to the time-reduced factorial covariance measure, and we exemplify its validity for various point processes, including the Poisson cluster, Hawkes, Neyman-Scott, and log-Gaussian Cox processes. Complementary to our upper bounds, we also derive matching lower bounds for various spatio-temporal point processes of interest and establish near minimax rate optimality of the empirical Kantorovich-Rubinstein distance.

Local Poisson Deconvolution for Discrete Signals

We analyze the statistical problem of recovering an atomic signal, modeled as a discrete uniform distribution $\mu$, from a binned Poisson convolution model. This question is motivated, among others, by super-resolution laser microscopy applications, where precise estimation of $\mu$ provides insights into spatial formations of cellular protein assemblies. Our main results quantify the local minimax risk of estimating $\mu$ for a broad class of smooth convolution kernels. This local perspective enables us to sharply quantify optimal estimation rates as a function of the clustering structure of the underlying signal. Moreover, our results are expressed under a multiscale loss function, which reveals that different parts of the underlying signal can be recovered at different rates depending on their local geometry. Overall, these results paint an optimistic perspective on the Poisson deconvolution problem, showing that accurate recovery is achievable under a much broader class of signals than suggested by existing global minimax analyses. Beyond Poisson deconvolution, our results also allow us to establish the local minimax rate of parameter estimation in Gaussian mixture models with uniform weights. We apply our methods to experimental super-resolution microscopy data to identify the location and configuration of individual DNA origamis. In addition, we complement our findings with numerical experiments on runtime and statistical recovery that showcase the practical performance of our estimators and their trade-offs.

Quick Adaptive Ternary Segmentation: An Efficient Decoding Procedure For Hidden Markov Models

Hidden Markov models (HMMs) are characterized by an unobservable (hidden) Markov chain and an observable process, which is a noisy version of the hidden chain. Decoding the original signal (i.e., hidden chain) from the noisy observations is one of the main goals in nearly all HMM based data analyses. Existing decoding algorithms such as the Viterbi algorithm have computational complexity at best linear in the length of the observed sequence, and sub-quadratic in the size of the state space of the Markov chain. We present Quick Adaptive Ternary Segmentation (QATS), a divide-and-conquer procedure which decodes the hidden sequence in polylogarithmic computational complexity in the length of the sequence, and cubic in the size of the state space, hence particularly suited for large scale HMMs with relatively few states. The procedure also suggests an effective way of data storage as specific cumulative sums. In essence, the estimated sequence of states sequentially maximizes local likelihood scores among all local paths with at most three segments. The maximization is performed only approximately using an adaptive search procedure. The resulting sequence is admissible in the sense that all transitions occur with positive probability. To complement formal results justifying our approach, we present Monte-Carlo simulations which demonstrate the speedups provided by QATS in comparison to Viterbi, along with a precision analysis of the returned sequences. An implementation of QATS in C++ is provided in the R-package QATS and is available from GitHub.

Optimistic search strategy: Change point detection for large-scale data via adaptive logarithmic queries

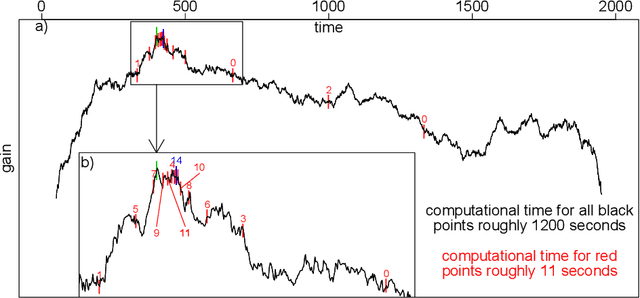
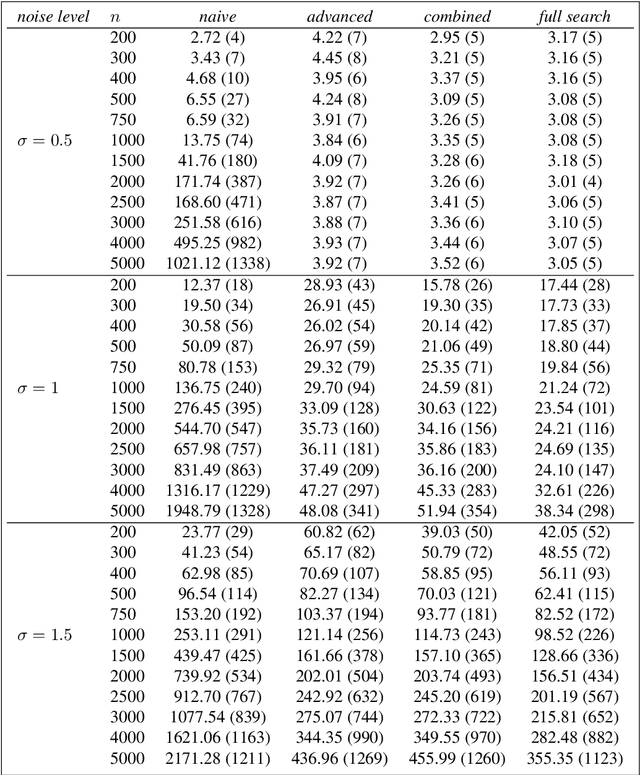
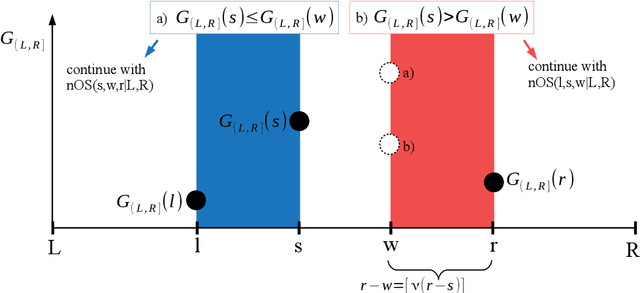
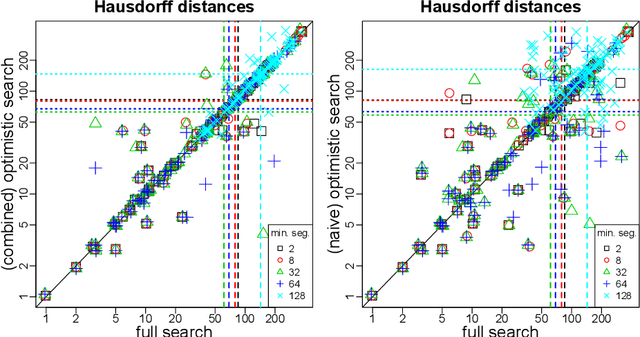
As a classical and ever reviving topic, change point detection is often formulated as a search for the maximum of a gain function describing improved fits when segmenting the data. Searching through all candidate split points on the grid for finding the best one requires $O(T)$ evaluations of the gain function for an interval with $T$ observations. If each evaluation is computationally demanding (e.g. in high-dimensional models), this can become infeasible. Instead, we propose optimistic search strategies with $O(\log T)$ evaluations exploiting specific structure of the gain function. Towards solid understanding of our strategies, we investigate in detail the classical univariate Gaussian change in mean setup. For some of our proposals we prove asymptotic minimax optimality for single and multiple change point scenarios. Our search strategies generalize far beyond the theoretically analyzed univariate setup. We illustrate, as an example, massive computational speedup in change point detection for high-dimensional Gaussian graphical models. More generally, we demonstrate empirically that our optimistic search methods lead to competitive estimation performance while heavily reducing run-time.

Statistical Multiresolution Estimation for Variational Imaging: With an Application in Poisson-Biophotonics

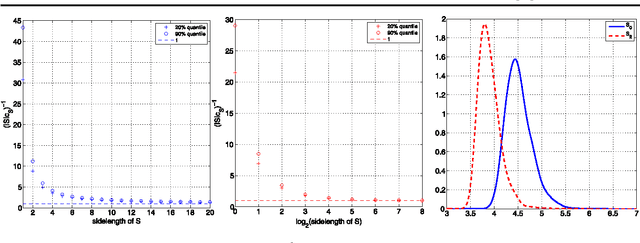
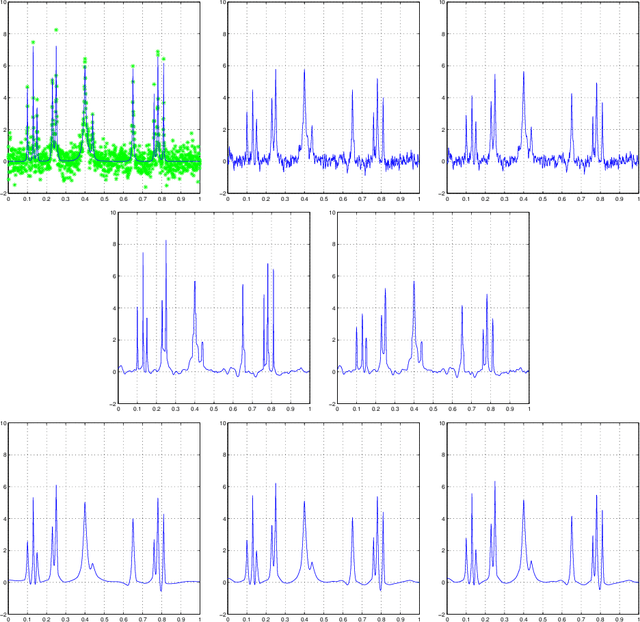
In this paper we present a spatially-adaptive method for image reconstruction that is based on the concept of statistical multiresolution estimation as introduced in [Frick K, Marnitz P, and Munk A. "Statistical multiresolution Dantzig estimation in imaging: Fundamental concepts and algorithmic framework". Electron. J. Stat., 6:231-268, 2012]. It constitutes a variational regularization technique that uses an supremum-type distance measure as data-fidelity combined with a convex cost functional. The resulting convex optimization problem is approached by a combination of an inexact alternating direction method of multipliers and Dykstra's projection algorithm. We describe a novel method for balancing data-fit and regularity that is fully automatic and allows for a sound statistical interpretation. The performance of our estimation approach is studied for various problems in imaging. Among others, this includes deconvolution problems that arise in Poisson nanoscale fluorescence microscopy.

Statistical Multiresolution Dantzig Estimation in Imaging: Fundamental Concepts and Algorithmic Framework

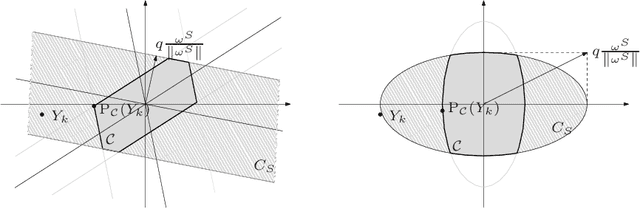
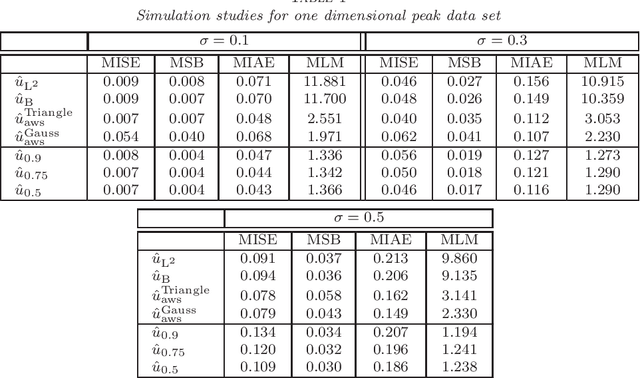
In this paper we are concerned with fully automatic and locally adaptive estimation of functions in a "signal + noise"-model where the regression function may additionally be blurred by a linear operator, e.g. by a convolution. To this end, we introduce a general class of statistical multiresolution estimators and develop an algorithmic framework for computing those. By this we mean estimators that are defined as solutions of convex optimization problems with supremum-type constraints. We employ a combination of the alternating direction method of multipliers with Dykstra's algorithm for computing orthogonal projections onto intersections of convex sets and prove numerical convergence. The capability of the proposed method is illustrated by various examples from imaging and signal detection.

Modeling the growth of fingerprints improves matching for adolescents

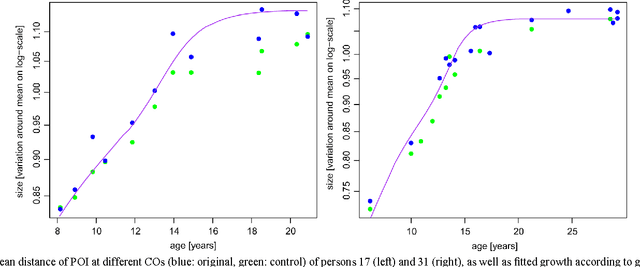
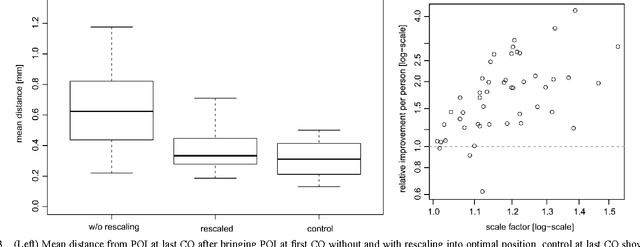
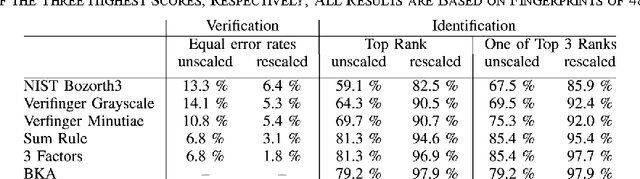
We study the effect of growth on the fingerprints of adolescents, based on which we suggest a simple method to adjust for growth when trying to recover a juvenile's fingerprint in a database years later. Based on longitudinal data sets in juveniles' criminal records, we show that growth essentially leads to an isotropic rescaling, so that we can use the strong correlation between growth in stature and limbs to model the growth of fingerprints proportional to stature growth as documented in growth charts. The proposed rescaling leads to a 72% reduction of the distances between corresponding minutiae for the data set analyzed. These findings were corroborated by several verification tests. In an identification test on a database containing 3.25 million right index fingers at the Federal Criminal Police Office of Germany, the identification error rate of 20.8% was reduced to 2.1% by rescaling. The presented method is of striking simplicity and can easily be integrated into existing automated fingerprint identification systems.

P-values for classification

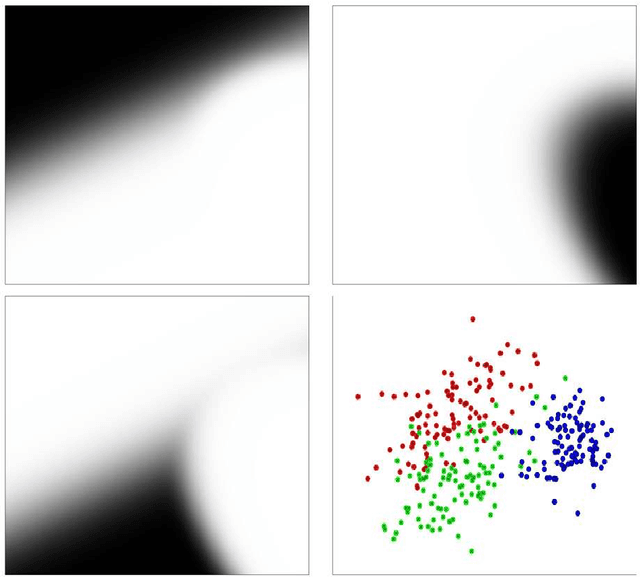
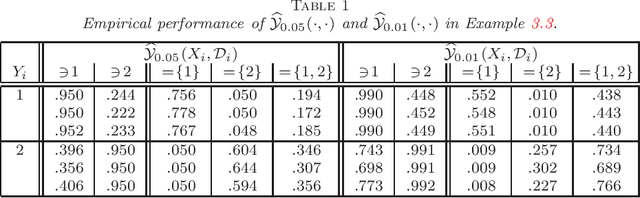
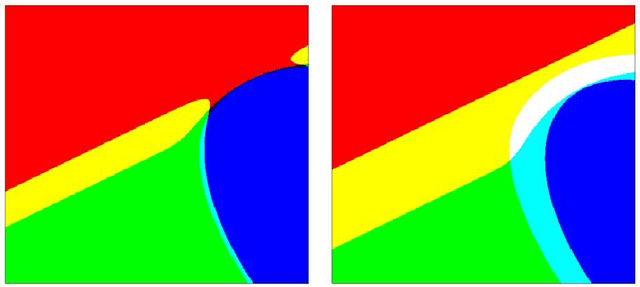
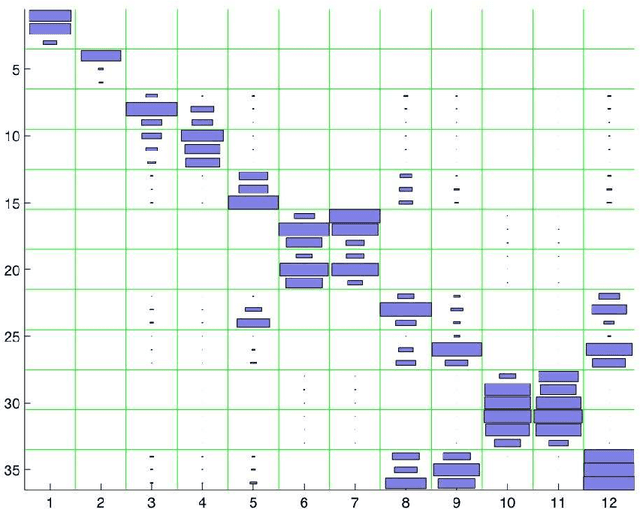
Let $(X,Y)$ be a random variable consisting of an observed feature vector $X\in \mathcal{X}$ and an unobserved class label $Y\in \{1,2,...,L\}$ with unknown joint distribution. In addition, let $\mathcal{D}$ be a training data set consisting of $n$ completely observed independent copies of $(X,Y)$. Usual classification procedures provide point predictors (classifiers) $\widehat{Y}(X,\mathcal{D})$ of $Y$ or estimate the conditional distribution of $Y$ given $X$. In order to quantify the certainty of classifying $X$ we propose to construct for each $\theta =1,2,...,L$ a p-value $\pi_{\theta}(X,\mathcal{D})$ for the null hypothesis that $Y=\theta$, treating $Y$ temporarily as a fixed parameter. In other words, the point predictor $\widehat{Y}(X,\mathcal{D})$ is replaced with a prediction region for $Y$ with a certain confidence. We argue that (i) this approach is advantageous over traditional approaches and (ii) any reasonable classifier can be modified to yield nonparametric p-values. We discuss issues such as optimality, single use and multiple use validity, as well as computational and graphical aspects.