Lorenz Haubner
Optimistic search strategy: Change point detection for large-scale data via adaptive logarithmic queries
Oct 20, 2020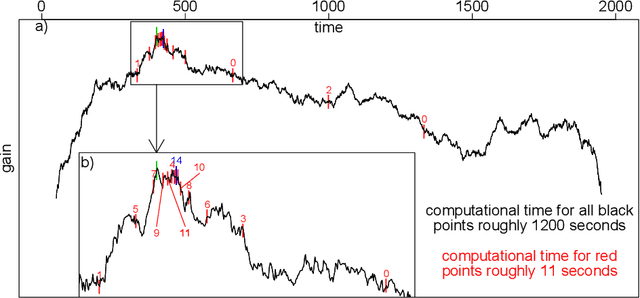
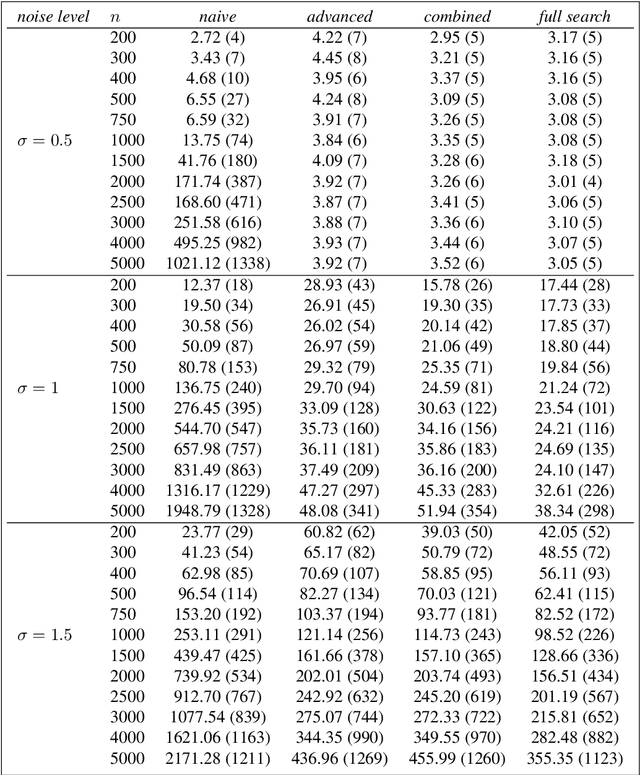
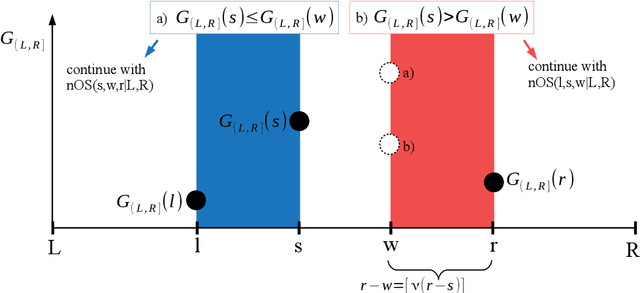
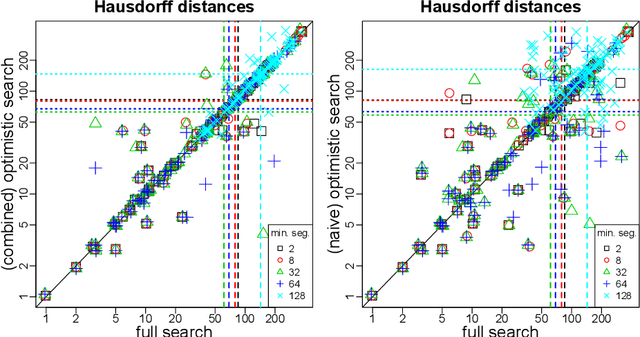
Abstract:As a classical and ever reviving topic, change point detection is often formulated as a search for the maximum of a gain function describing improved fits when segmenting the data. Searching through all candidate split points on the grid for finding the best one requires $O(T)$ evaluations of the gain function for an interval with $T$ observations. If each evaluation is computationally demanding (e.g. in high-dimensional models), this can become infeasible. Instead, we propose optimistic search strategies with $O(\log T)$ evaluations exploiting specific structure of the gain function. Towards solid understanding of our strategies, we investigate in detail the classical univariate Gaussian change in mean setup. For some of our proposals we prove asymptotic minimax optimality for single and multiple change point scenarios. Our search strategies generalize far beyond the theoretically analyzed univariate setup. We illustrate, as an example, massive computational speedup in change point detection for high-dimensional Gaussian graphical models. More generally, we demonstrate empirically that our optimistic search methods lead to competitive estimation performance while heavily reducing run-time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge