Random Forests for Change Point Detection

We propose a novel multivariate nonparametric multiple change point detection method using classifiers. We construct a classifier log-likelihood ratio that uses class probability predictions to compare different change point configurations. We propose a computationally feasible search method that is particularly well suited for random forests, denoted by changeforest. However, the method can be paired with any classifier that yields class probability predictions, which we illustrate by also using a k-nearest neighbor classifier. We provide theoretical results motivating our choices. In a large simulation study, our proposed changeforest method achieves improved empirical performance compared to existing multivariate nonparametric change point detection methods. An efficient implementation of our method is made available for R, Python, and Rust users in the changeforest software package.

Optimistic search strategy: Change point detection for large-scale data via adaptive logarithmic queries

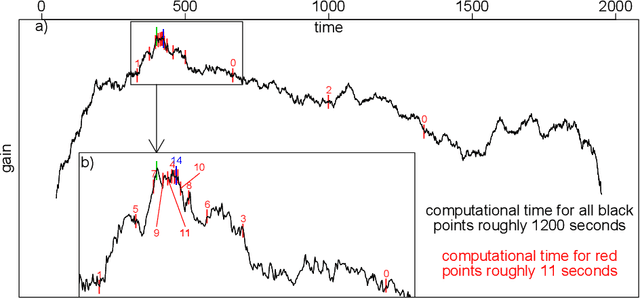
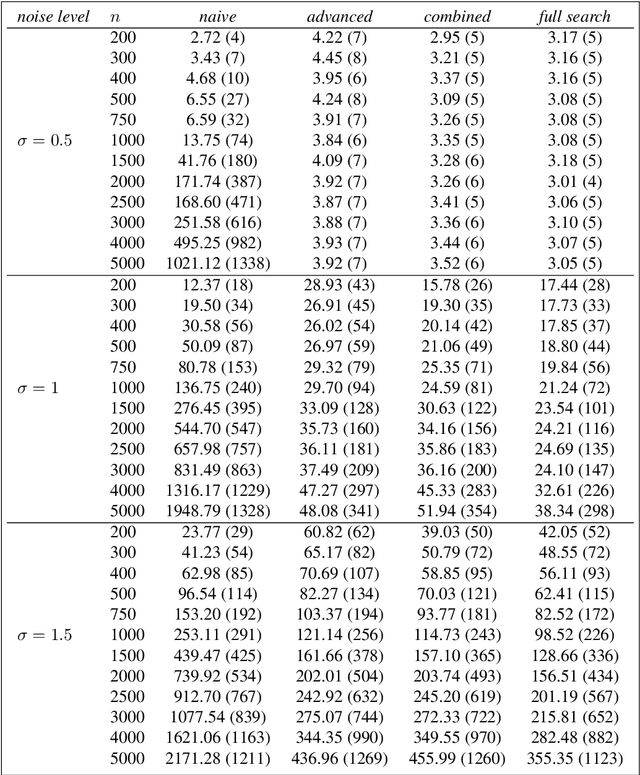
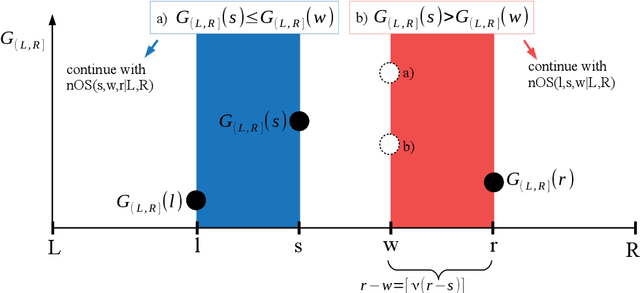
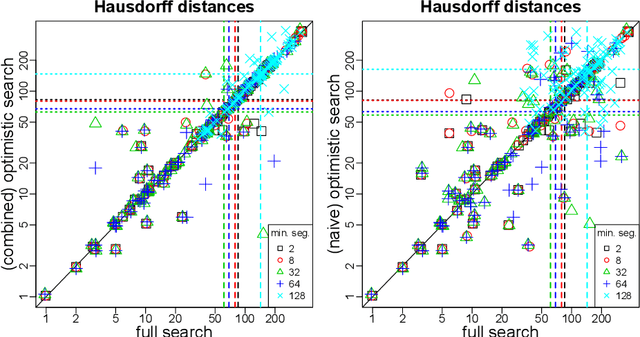
As a classical and ever reviving topic, change point detection is often formulated as a search for the maximum of a gain function describing improved fits when segmenting the data. Searching through all candidate split points on the grid for finding the best one requires $O(T)$ evaluations of the gain function for an interval with $T$ observations. If each evaluation is computationally demanding (e.g. in high-dimensional models), this can become infeasible. Instead, we propose optimistic search strategies with $O(\log T)$ evaluations exploiting specific structure of the gain function. Towards solid understanding of our strategies, we investigate in detail the classical univariate Gaussian change in mean setup. For some of our proposals we prove asymptotic minimax optimality for single and multiple change point scenarios. Our search strategies generalize far beyond the theoretically analyzed univariate setup. We illustrate, as an example, massive computational speedup in change point detection for high-dimensional Gaussian graphical models. More generally, we demonstrate empirically that our optimistic search methods lead to competitive estimation performance while heavily reducing run-time.

Change point detection for graphical models in presence of missing values

We propose estimation methods for change points in high-dimensional covariance structures with an emphasis on challenging scenarios with missing values. We advocate three imputation like methods and investigate their implications on common losses used for change point detection. We also discuss how model selection methods have to be adapted to the setting of incomplete data. The methods are compared in a simulation study and applied to real data examples from environmental monitoring systems as well as financial time series.