Thomas Hotz
Quantifying the Resolution of a Template after Image Registration
Feb 27, 2024Abstract:In many image processing applications (e.g. computational anatomy) a groupwise registration is performed on a sample of images and a template image is simultaneously generated. From the template alone it is in general unclear to which extent the registered images are still misaligned, which means that some regions of the template represent the structural features in the sample images less reliably than others. In a sense, the template exhibits a lower resolution there. Guided by characteristic examples of misaligned image features in one dimension, we develop a visual measure to quantify the resolution at each location of a template which is based on the observation that misalignments between the registered sample images are reduced by smoothing with the strength of the smoothing being related to the magnitude of the misalignment. Finally the resulting resolution measure is applied to example datasets in two and three dimensions. The corresponding code is publicly available on GitHub.
Manifolds of Projective Shapes
Nov 05, 2018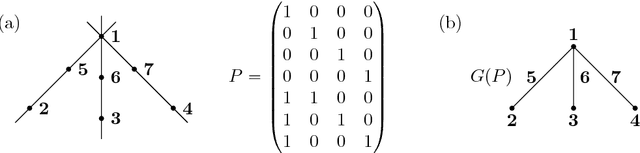
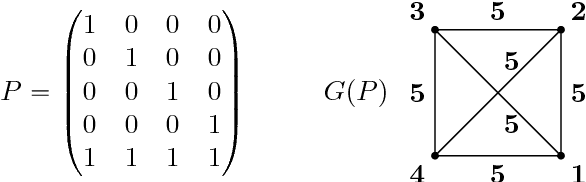
Abstract:The projective shape of a configuration of k points or "landmarks" in RP(d) consists of the information that is invariant under projective transformations and hence is reconstructable from uncalibrated camera views. Mathematically, the space of projective shapes for these k landmarks can be described as the quotient space of k copies of RP(d) modulo the action of the projective linear group PGL(d). Using homogeneous coordinates, such configurations can be described as real k-times-(d+1)-dimensional matrices given up to left-multiplication of non-singular diagonal matrices, while the group PGL(d) acts as GL(d+1) from the right. The main purpose of this paper is to give a detailed examination of the topology of projective shape space, and, using matrix notation, it is shown how to derive subsets that are in a certain sense maximal, differentiable Hausdorff manifolds which can be provided with a Riemannian metric. A special subclass of the projective shapes consists of the Tyler regular shapes, for which geometrically motivated pre-shapes can be defined, thus allowing for the construction of a natural Riemannian metric.
Modeling the growth of fingerprints improves matching for adolescents
Aug 06, 2010
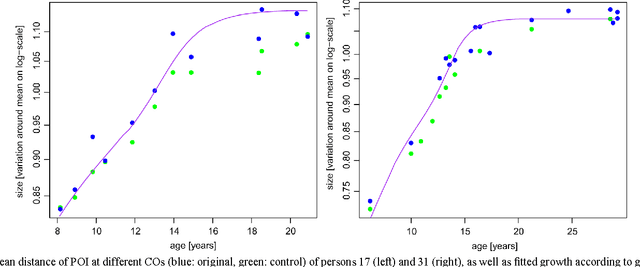
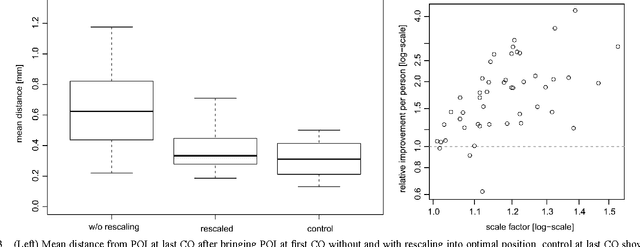
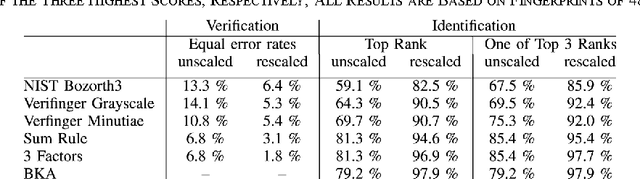
Abstract:We study the effect of growth on the fingerprints of adolescents, based on which we suggest a simple method to adjust for growth when trying to recover a juvenile's fingerprint in a database years later. Based on longitudinal data sets in juveniles' criminal records, we show that growth essentially leads to an isotropic rescaling, so that we can use the strong correlation between growth in stature and limbs to model the growth of fingerprints proportional to stature growth as documented in growth charts. The proposed rescaling leads to a 72% reduction of the distances between corresponding minutiae for the data set analyzed. These findings were corroborated by several verification tests. In an identification test on a database containing 3.25 million right index fingers at the Federal Criminal Police Office of Germany, the identification error rate of 20.8% was reduced to 2.1% by rescaling. The presented method is of striking simplicity and can easily be integrated into existing automated fingerprint identification systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge