Florian Kelma
Manifolds of Projective Shapes
Nov 05, 2018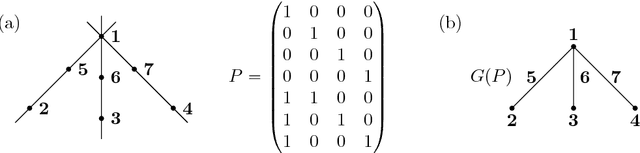
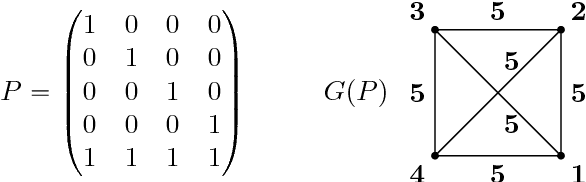
Abstract:The projective shape of a configuration of k points or "landmarks" in RP(d) consists of the information that is invariant under projective transformations and hence is reconstructable from uncalibrated camera views. Mathematically, the space of projective shapes for these k landmarks can be described as the quotient space of k copies of RP(d) modulo the action of the projective linear group PGL(d). Using homogeneous coordinates, such configurations can be described as real k-times-(d+1)-dimensional matrices given up to left-multiplication of non-singular diagonal matrices, while the group PGL(d) acts as GL(d+1) from the right. The main purpose of this paper is to give a detailed examination of the topology of projective shape space, and, using matrix notation, it is shown how to derive subsets that are in a certain sense maximal, differentiable Hausdorff manifolds which can be provided with a Riemannian metric. A special subclass of the projective shapes consists of the Tyler regular shapes, for which geometrically motivated pre-shapes can be defined, thus allowing for the construction of a natural Riemannian metric.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge