Fast ground-to-air transition with avian-inspired multifunctional legs

Most birds can navigate seamlessly between aerial and terrestrial environments. Whereas the forelimbs evolved into wings primarily for flight, the hindlimbs serve diverse functions such as walking, hopping, and leaping, and jumping take-off for transitions into flight. These capabilities have inspired engineers to aim for similar multi-modality in aerial robots, expanding their range of applications across diverse environments. However, challenges remain in reproducing multi-modal locomotion, across gaits with distinct kinematics and propulsive characteristics, such as walking and jumping, while preserving lightweight mass for flight. This tradeoff between mechanical complexity and versatility limits most existing aerial robots to only one additional locomotor mode. Here, we overcome the complexity-versatility tradeoff with RAVEN (Robotic Avian-inspired Vehicle for multiple ENvironments), which uses its bird-inspired multi-functional legs to jump rapidly into flight, walk on ground and hop over obstacles and gaps similar to the multi-modal locomotion of birds. We show that jumping for take-off contributes substantially to initial flight take-off speed and, remarkably, that it is more energy-efficient than solely propeller-based take-off. Our analysis suggests an important tradeoff in mass distribution between legs and body among birds adapted for different locomotor strategies, with greater investment in leg mass among terrestrial birds with multi-modal gait demands. Multi-functional robot legs expand opportunities to deploy traditional fixed-wing aircraft in complex terrains through autonomous take-offs and multi-modal gaits.

Crash-perching on vertical poles with a hugging-wing robot

Perching with winged Unmanned Aerial Vehicles has often been solved by means of complex control or intricate appendages. Here, we present a simple yet novel method that relies on passive wing morphing for crash-landing on trees and other types of vertical poles. Inspired by the adaptability of animals' and bats' limbs in gripping and holding onto trees, we design dual-purpose wings that enable both aerial gliding and perching on poles. With an upturned nose design, the robot can passively reorient from horizontal flight to vertical upon a head-on crash with a pole, followed by hugging with its wings to perch. We characterize the performance of reorientation and perching in terms of impact speed and angle, pole material, and size. The robot robustly reorients at impact angles above 15{\deg} and speeds of 3 m/s to 9 m/s, and can hold onto various pole types larger than 28% of its wingspan in diameter. We demonstrate crash-perching on tree trunks with an overall success rate of 71%. The method opens up new possibilities for the use of aerial robots in applications such as inspection, maintenance, and biodiversity conservation.

Imprecise dynamic walking with time-projection control

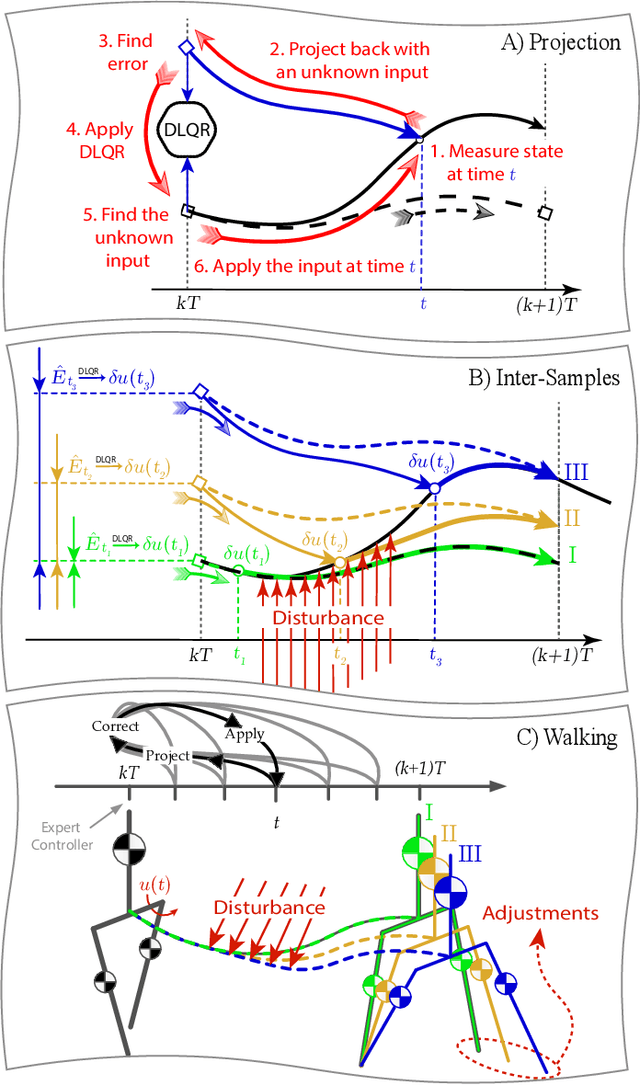
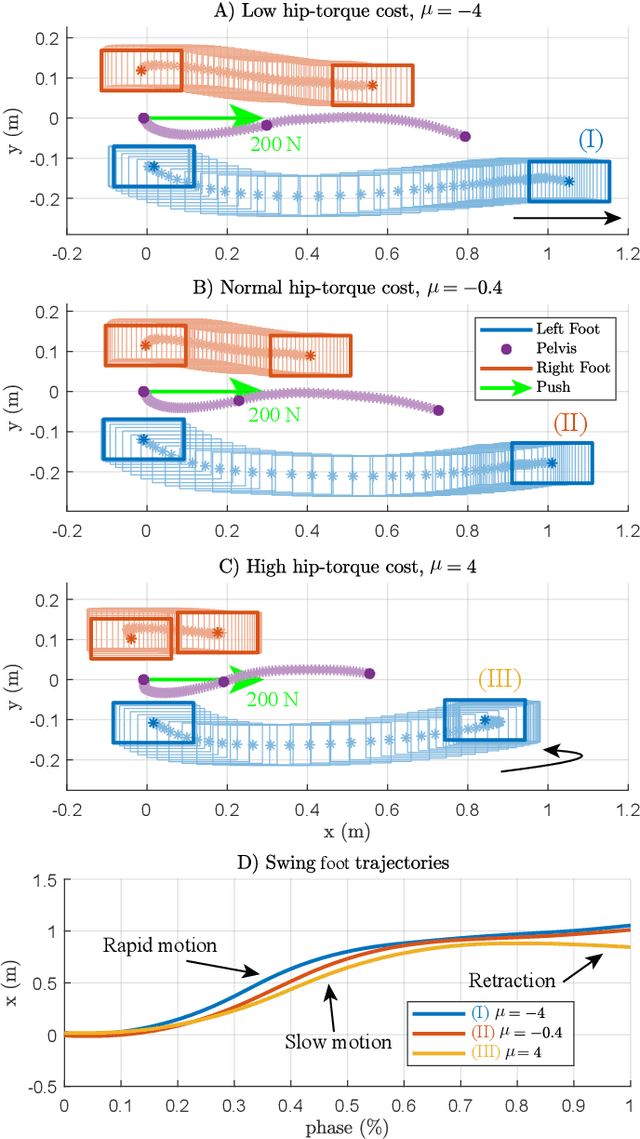
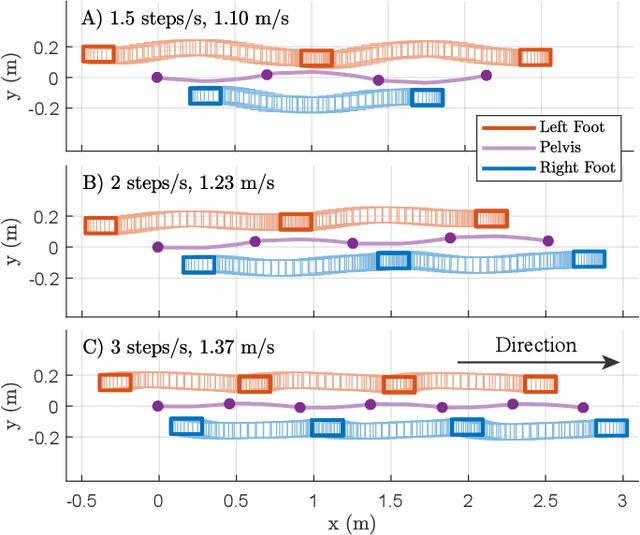
We present a new walking foot-placement controller based on 3LP, a 3D model of bipedal walking that is composed of three pendulums to simulate falling, swing and torso dynamics. Taking advantage of linear equations and closed-form solutions of the 3LP model, our proposed controller projects intermediate states of the biped back to the beginning of the phase for which a discrete LQR controller is designed. After the projection, a proper control policy is generated by this LQR controller and used at the intermediate time. This control paradigm reacts to disturbances immediately and includes rules to account for swing dynamics and leg-retraction. We apply it to a simulated Atlas robot in position-control, always commanded to perform in-place walking. The stance hip joint in our robot keeps the torso upright to let the robot naturally fall, and the swing hip joint tracks the desired footstep location. Combined with simple Center of Pressure (CoP) damping rules in the low-level controller, our foot-placement enables the robot to recover from strong pushes and produce periodic walking gaits when subject to persistent sources of disturbance, externally or internally. These gaits are imprecise, i.e., emergent from asymmetry sources rather than precisely imposing a desired velocity to the robot. Also in extreme conditions, restricting linearity assumptions of the 3LP model are often violated, but the system remains robust in our simulations. An extensive analysis of closed-loop eigenvalues, viable regions and sensitivity to push timings further demonstrate the strengths of our simple controller.

Push recovery with stepping strategy based on time-projection control

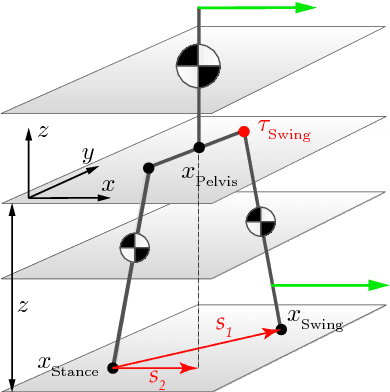
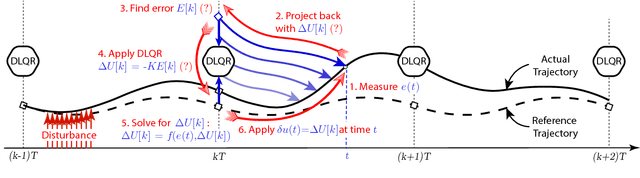
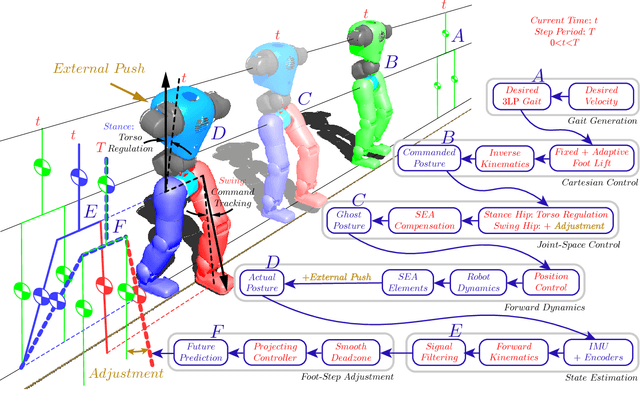
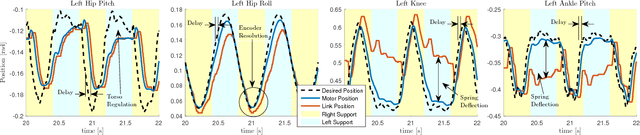
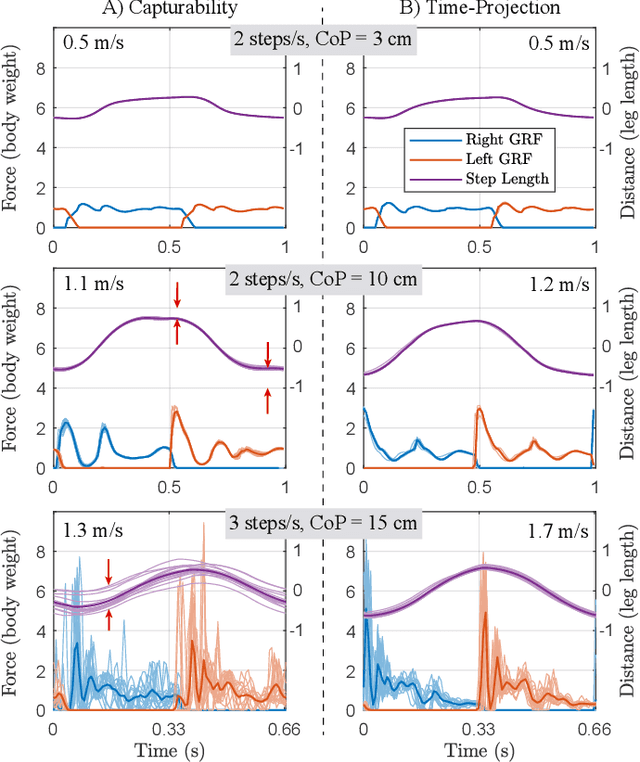
In this paper, we present a simple control framework for on-line push recovery with dynamic stepping properties. Due to relatively heavy legs in our robot, we need to take swing dynamics into account and thus use a linear model called 3LP which is composed of three pendulums to simulate swing and torso dynamics. Based on 3LP equations, we formulate discrete LQR controllers and use a particular time-projection method to adjust the next footstep location on-line during the motion continuously. This adjustment, which is found based on both pelvis and swing foot tracking errors, naturally takes the swing dynamics into account. Suggested adjustments are added to the Cartesian 3LP gaits and converted to joint-space trajectories through inverse kinematics. Fixed and adaptive foot lift strategies also ensure enough ground clearance in perturbed walking conditions. The proposed structure is robust, yet uses very simple state estimation and basic position tracking. We rely on the physical series elastic actuators to absorb impacts while introducing simple laws to compensate their tracking bias. Extensive experiments demonstrate the functionality of different control blocks and prove the effectiveness of time-projection in extreme push recovery scenarios. We also show self-produced and emergent walking gaits when the robot is subject to continuous dragging forces. These gaits feature dynamic walking robustness due to relatively soft springs in the ankles and avoiding any Zero Moment Point (ZMP) control in our proposed architecture.

Time-projection control to recover inter-sample disturbances, application to bipedal walking control

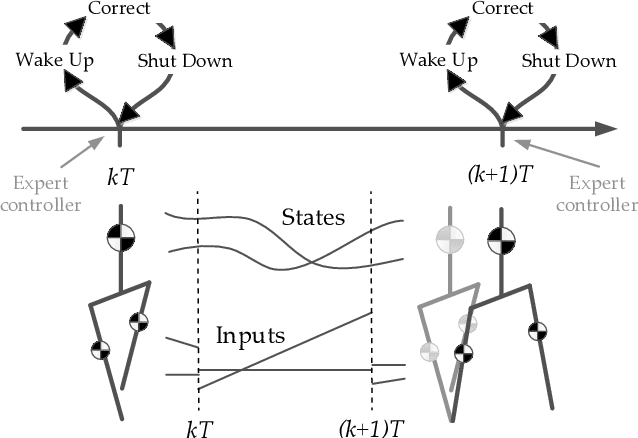
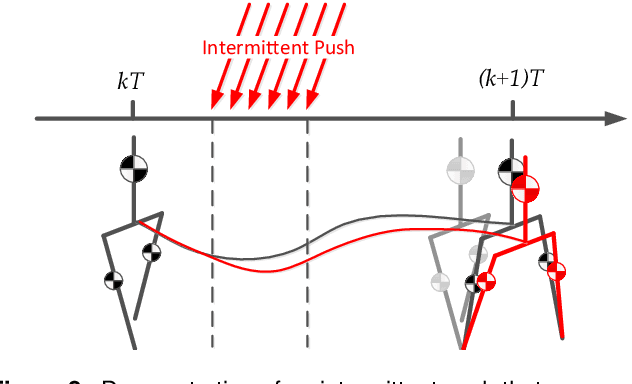
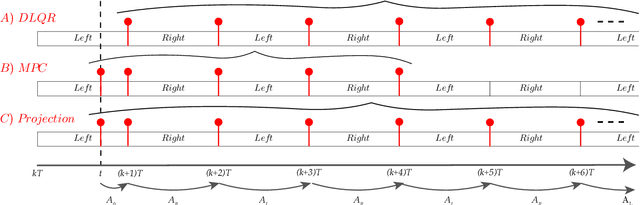
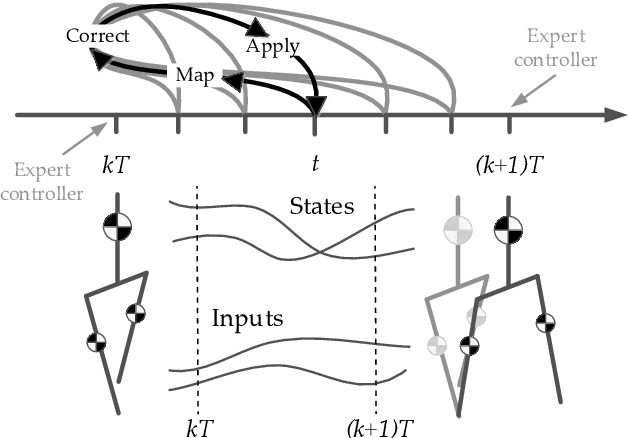
We present a new walking controller based on 3LP, a 3D model of bipedal walking that is composed of three pendulums to simulate falling, swing and torso dynamics. Taking advantage of linear equations and closed-form solutions of 3LP, the proposed controller projects intermediate states of the biped back to the beginning of the phase for which a discrete LQR controller is designed. After the projection, a proper control policy is generated by this LQR controller and used at the intermediate time. The projection controller reacts to disturbances immediately and compared to the discrete LQR controller, it provides superior performance in recovering intermittent external pushes. Further analysis of closed-loop eigenvalues and disturbance rejection strength show strong stabilization properties for this architecture. An analysis of viable regions also show that the proposed controller covers most of the maximal viable set of states. It is computationally much faster than Model Predictive Controllers (MPC) and yet optimal over an infinite horizon.

A new time-projecting controller based on 3LP model to recover intermittent pushes

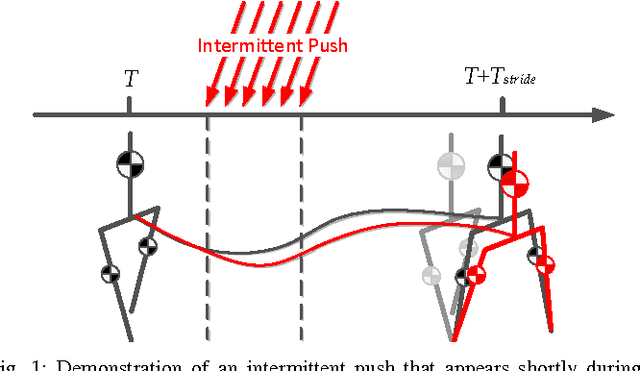
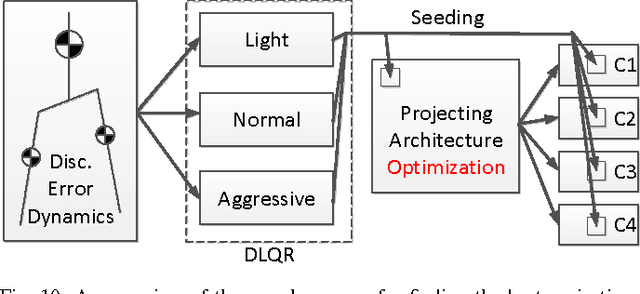
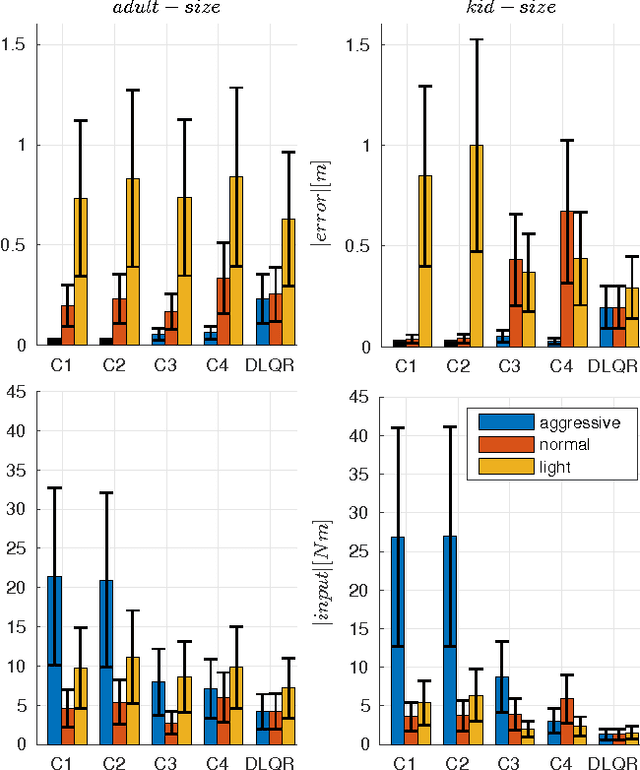
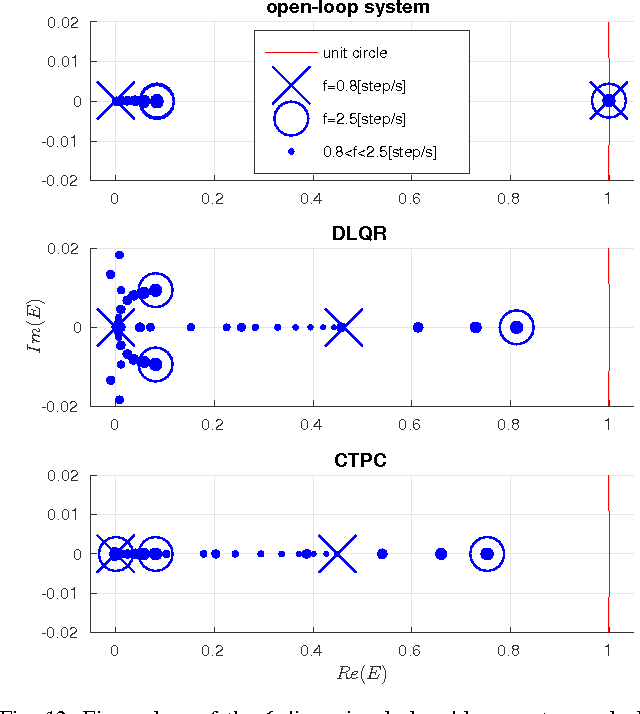
In this paper, we present a new walking controller based on 3LP model. Taking advantage of linear equations and closed-form solutions of 3LP, the proposed controller can project the state of the robot at any time during the phase back to a certain event for which, a discrete LQR controller is designed. After the projection, a proper control policy is generated by the expert discrete controller and used online. This projecting architecture reacts to disturbances with minimal delay and compared to discrete controllers, it provides superior performance in recovering intermittent external pushes. Further analysis of closed-loop eigenvalues and disturbance rejection shows that the proposed time-projecting controller has strong stabilization properties. Controllable regions also show that the projecting architecture covers most of the maximal controllable set of states. It is computationally much faster than model predictive controllers, but still optimal.

3LP: a linear 3D-walking model including torso and swing dynamics

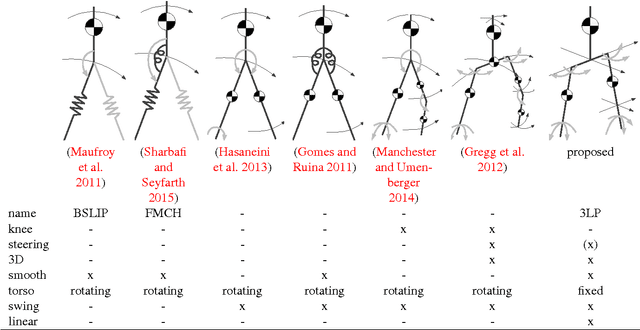
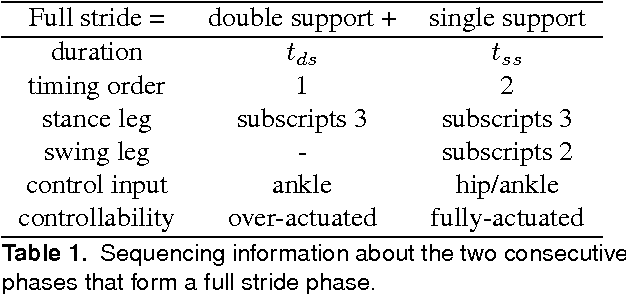
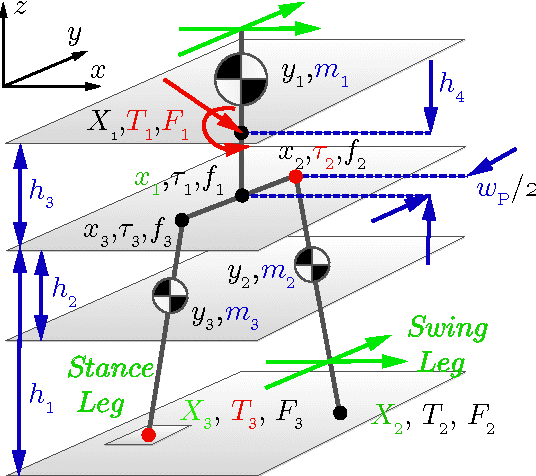
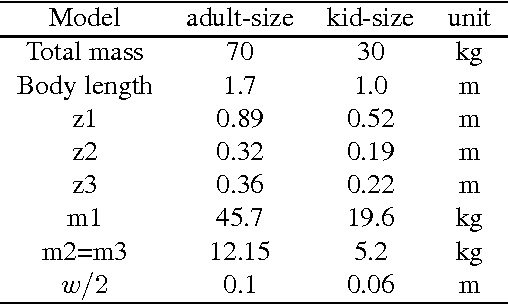
In this paper, we present a new model of biped locomotion which is composed of three linear pendulums (one per leg and one for the whole upper body) to describe stance, swing and torso dynamics. In addition to double support, this model has different actuation possibilities in the swing hip and stance ankle which could be widely used to produce different walking gaits. Without the need for numerical time-integration, closed-form solutions help finding periodic gaits which could be simply scaled in certain dimensions to modulate the motion online. Thanks to linearity properties, the proposed model can provide a computationally fast platform for model predictive controllers to predict the future and consider meaningful inequality constraints to ensure feasibility of the motion. Such property is coming from describing dynamics with joint torques directly and therefore, reflecting hardware limitations more precisely, even in the very abstract high level template space. The proposed model produces human-like torque and ground reaction force profiles and thus, compared to point-mass models, it is more promising for precise control of humanoid robots. Despite being linear and lacking many other features of human walking like CoM excursion, knee flexion and ground clearance, we show that the proposed model can predict one of the main optimality trends in human walking, i.e. nonlinear speed-frequency relationship. In this paper, we mainly focus on describing the model and its capabilities, comparing it with human data and calculating optimal human gait variables. Setting up control problems and advanced biomechanical analysis still remain for future works.