A new time-projecting controller based on 3LP model to recover intermittent pushes
Paper and Code
May 10, 2016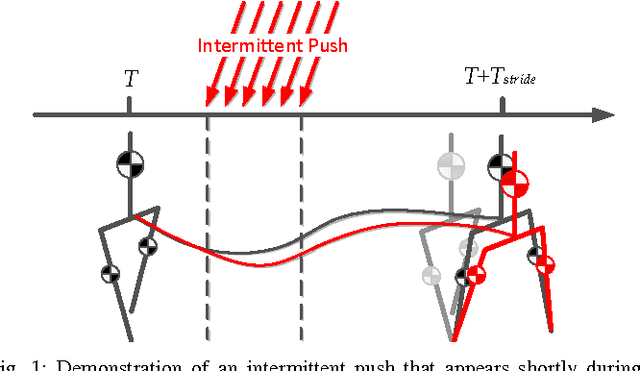
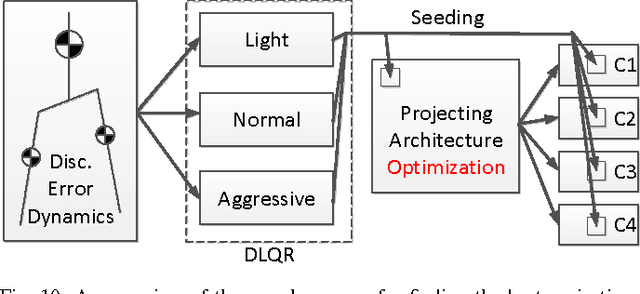
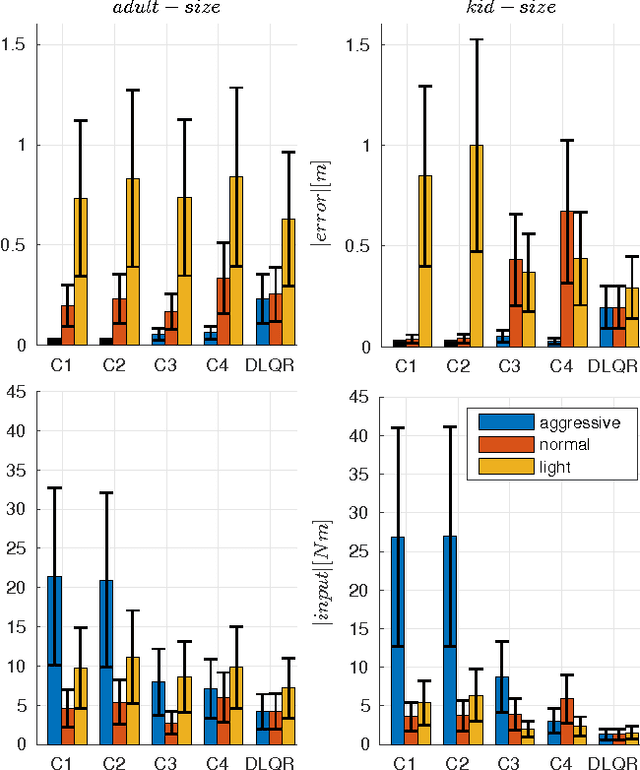
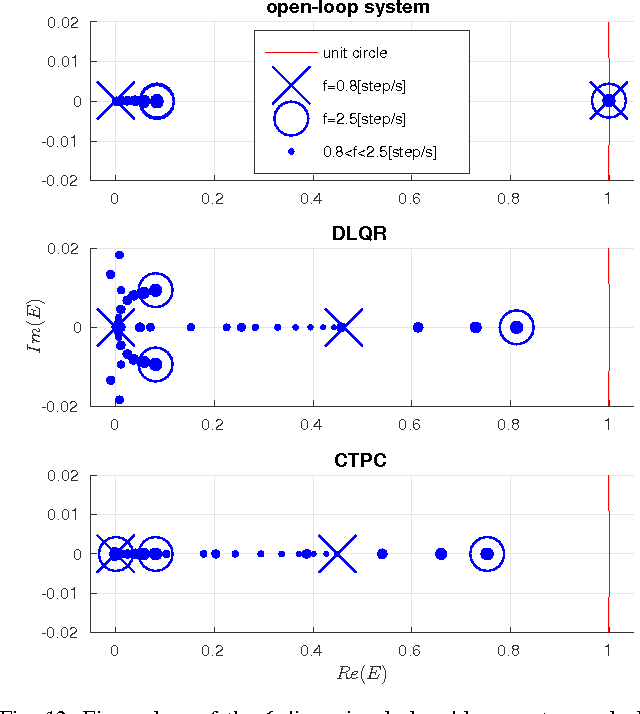
In this paper, we present a new walking controller based on 3LP model. Taking advantage of linear equations and closed-form solutions of 3LP, the proposed controller can project the state of the robot at any time during the phase back to a certain event for which, a discrete LQR controller is designed. After the projection, a proper control policy is generated by the expert discrete controller and used online. This projecting architecture reacts to disturbances with minimal delay and compared to discrete controllers, it provides superior performance in recovering intermittent external pushes. Further analysis of closed-loop eigenvalues and disturbance rejection shows that the proposed time-projecting controller has strong stabilization properties. Controllable regions also show that the projecting architecture covers most of the maximal controllable set of states. It is computationally much faster than model predictive controllers, but still optimal.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge