Push recovery with stepping strategy based on time-projection control

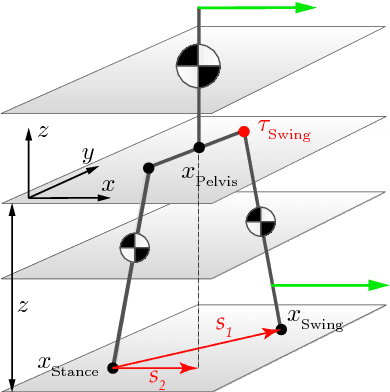
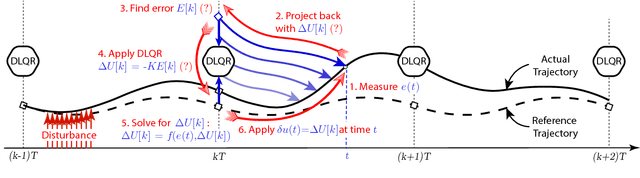
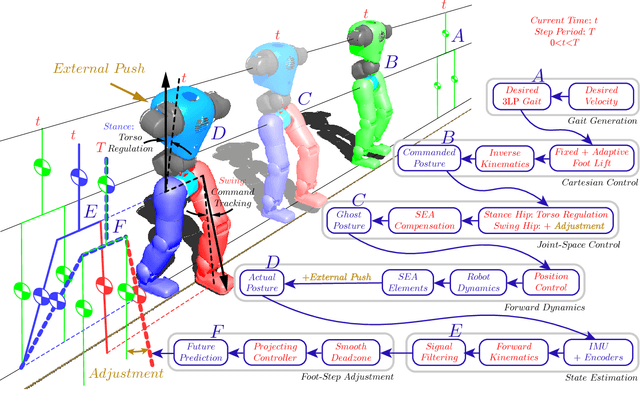
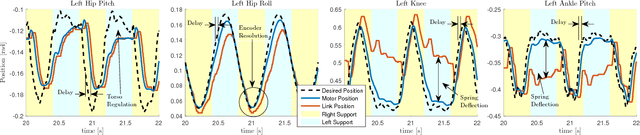
In this paper, we present a simple control framework for on-line push recovery with dynamic stepping properties. Due to relatively heavy legs in our robot, we need to take swing dynamics into account and thus use a linear model called 3LP which is composed of three pendulums to simulate swing and torso dynamics. Based on 3LP equations, we formulate discrete LQR controllers and use a particular time-projection method to adjust the next footstep location on-line during the motion continuously. This adjustment, which is found based on both pelvis and swing foot tracking errors, naturally takes the swing dynamics into account. Suggested adjustments are added to the Cartesian 3LP gaits and converted to joint-space trajectories through inverse kinematics. Fixed and adaptive foot lift strategies also ensure enough ground clearance in perturbed walking conditions. The proposed structure is robust, yet uses very simple state estimation and basic position tracking. We rely on the physical series elastic actuators to absorb impacts while introducing simple laws to compensate their tracking bias. Extensive experiments demonstrate the functionality of different control blocks and prove the effectiveness of time-projection in extreme push recovery scenarios. We also show self-produced and emergent walking gaits when the robot is subject to continuous dragging forces. These gaits feature dynamic walking robustness due to relatively soft springs in the ankles and avoiding any Zero Moment Point (ZMP) control in our proposed architecture.

Self-synchronization and Self-stabilization of 3D Bipedal Walking Gaits

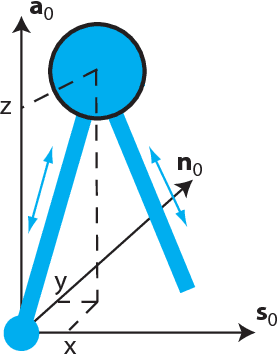
This paper seeks insight into stabilization mechanisms for periodic walking gaits in 3D bipedal robots. Based on this insight, a control strategy based on virtual constraints, which imposes coordination between joints rather than a temporal evolution, will be proposed for achieving asymptotic convergence toward a periodic motion. For planar bipeds with one degree of underactuation, it is known that a vertical displacement of the center of mass---with downward velocity at the step transition---induces stability of a walking gait. This paper concerns the qualitative extension of this type of property to 3D walking with two degrees of underactuation. It is shown that a condition on the position of the center of mass in the horizontal plane at the transition between steps induces synchronization between the motions in the sagittal and frontal planes. A combination of the conditions for self-synchronization and vertical oscillations leads to stable gaits. The algorithm for self-stabilization of 3D walking gaits is first developed for a simplified model of a walking robot (an inverted pendulum with variable length legs), and then it is extended to a complex model of the humanoid robot Romeo using the notion of Hybrid Zero Dynamics. Simulations of the model of the robot illustrate the efficacy of the method and its robustness.

Restricted Discrete Invariance and Self-Synchronization For Stable Walking of Bipedal Robots

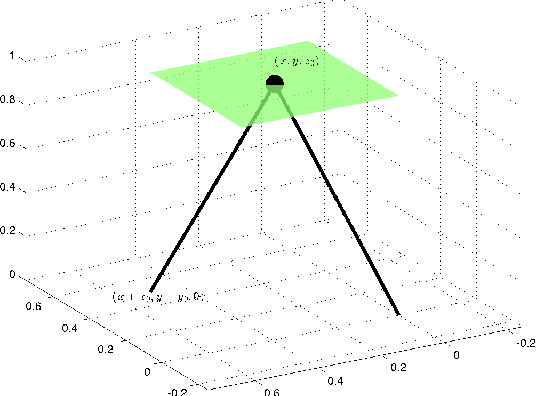
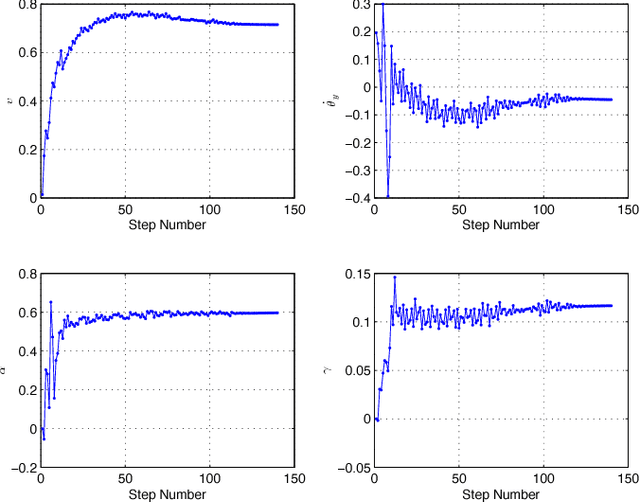
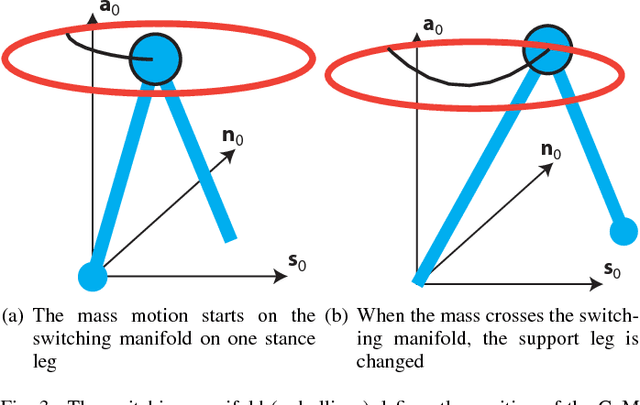
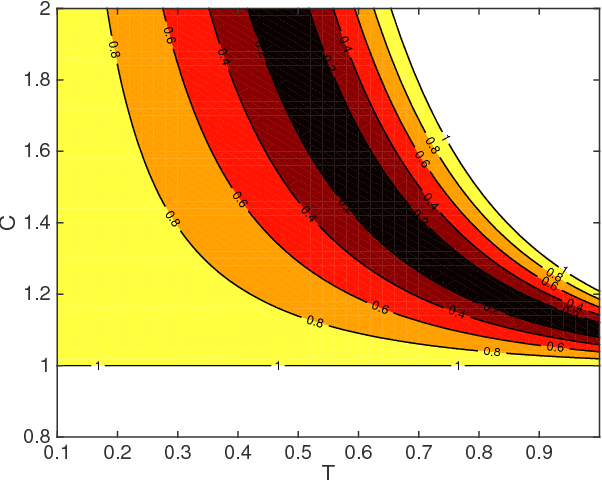
Models of bipedal locomotion are hybrid, with a continuous component often generated by a Lagrangian plus actuators, and a discrete component where leg transfer takes place. The discrete component typically consists of a locally embedded co-dimension one submanifold in the continuous state space of the robot, called the switching surface, and a reset map that provides a new initial condition when a solution of the continuous component intersects the switching surface. The aim of this paper is to identify a low-dimensional submanifold of the switching surface, which, when it can be rendered invariant by the closed-loop dynamics, leads to asymptotically stable periodic gaits. The paper begins this process by studying the well-known 3D Linear Inverted Pendulum (LIP) model, where analytical results are much easier to obtain. A key contribution here is the notion of \textit{self-synchronization}, which refers to the periods of the pendular motions in the sagittal and frontal planes tending to a common period. The notion of invariance resulting from the study of the 3D LIP model is then extended to a 9-DOF 3D biped. A numerical study is performed to illustrate that asymptotically stable walking may be obtained.