Self-synchronization and Self-stabilization of 3D Bipedal Walking Gaits
Paper and Code
Jul 07, 2017
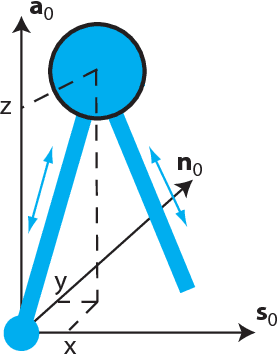
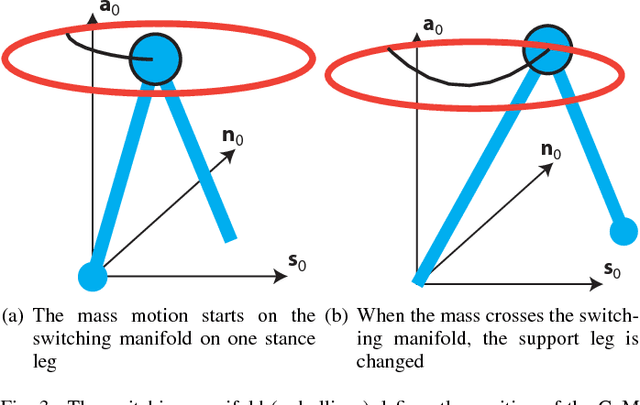
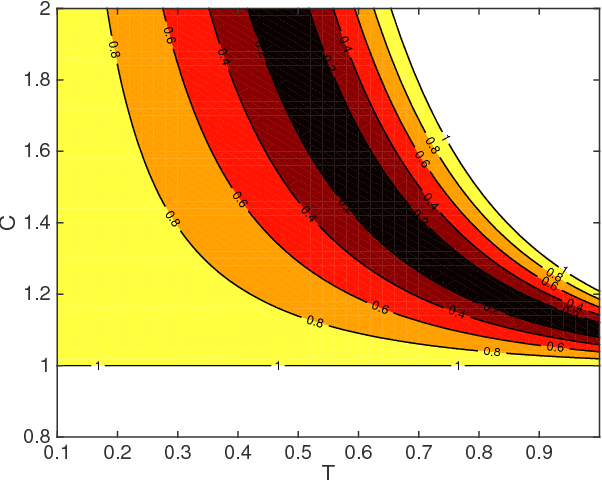
This paper seeks insight into stabilization mechanisms for periodic walking gaits in 3D bipedal robots. Based on this insight, a control strategy based on virtual constraints, which imposes coordination between joints rather than a temporal evolution, will be proposed for achieving asymptotic convergence toward a periodic motion. For planar bipeds with one degree of underactuation, it is known that a vertical displacement of the center of mass---with downward velocity at the step transition---induces stability of a walking gait. This paper concerns the qualitative extension of this type of property to 3D walking with two degrees of underactuation. It is shown that a condition on the position of the center of mass in the horizontal plane at the transition between steps induces synchronization between the motions in the sagittal and frontal planes. A combination of the conditions for self-synchronization and vertical oscillations leads to stable gaits. The algorithm for self-stabilization of 3D walking gaits is first developed for a simplified model of a walking robot (an inverted pendulum with variable length legs), and then it is extended to a complex model of the humanoid robot Romeo using the notion of Hybrid Zero Dynamics. Simulations of the model of the robot illustrate the efficacy of the method and its robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge