Restricted Discrete Invariance and Self-Synchronization For Stable Walking of Bipedal Robots

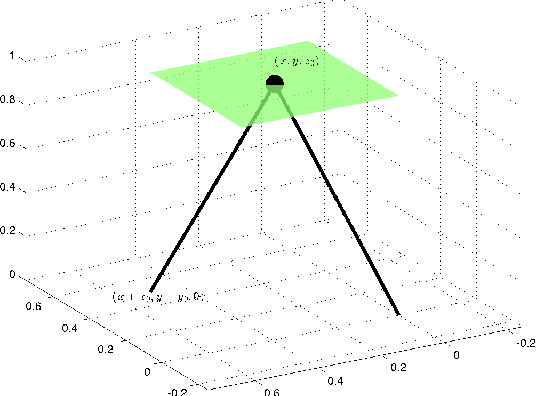
Models of bipedal locomotion are hybrid, with a continuous component often generated by a Lagrangian plus actuators, and a discrete component where leg transfer takes place. The discrete component typically consists of a locally embedded co-dimension one submanifold in the continuous state space of the robot, called the switching surface, and a reset map that provides a new initial condition when a solution of the continuous component intersects the switching surface. The aim of this paper is to identify a low-dimensional submanifold of the switching surface, which, when it can be rendered invariant by the closed-loop dynamics, leads to asymptotically stable periodic gaits. The paper begins this process by studying the well-known 3D Linear Inverted Pendulum (LIP) model, where analytical results are much easier to obtain. A key contribution here is the notion of \textit{self-synchronization}, which refers to the periods of the pendular motions in the sagittal and frontal planes tending to a common period. The notion of invariance resulting from the study of the 3D LIP model is then extended to a 9-DOF 3D biped. A numerical study is performed to illustrate that asymptotically stable walking may be obtained.

Torque Saturation in Bipedal Robotic Walking through Control Lyapunov Function Based Quadratic Programs

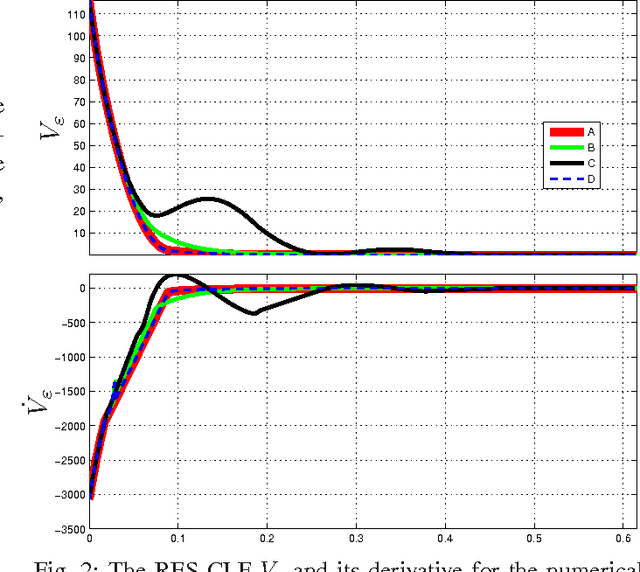
This paper presents a novel method for directly incorporating user-defined control input saturations into the calculation of a control Lyapunov function (CLF)-based walking controller for a biped robot. Previous work by the authors has demonstrated the effectiveness of CLF controllers for stabilizing periodic gaits for biped walkers, and the current work expands on those results by providing a more effective means for handling control saturations. The new approach, based on a convex optimization routine running at a 1 kHz control update rate, is useful not only for handling torque saturations but also for incorporating a whole family of user-defined constraints into the online computation of a CLF controller. The paper concludes with an experimental implementation of the main results on the bipedal robot MABEL.