Imprecise dynamic walking with time-projection control

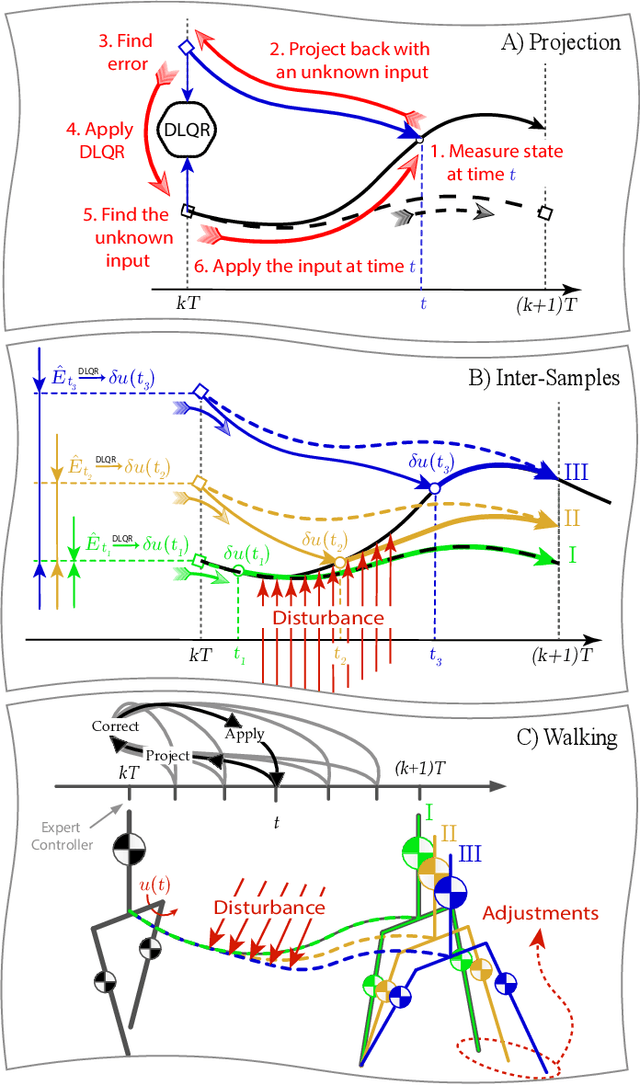
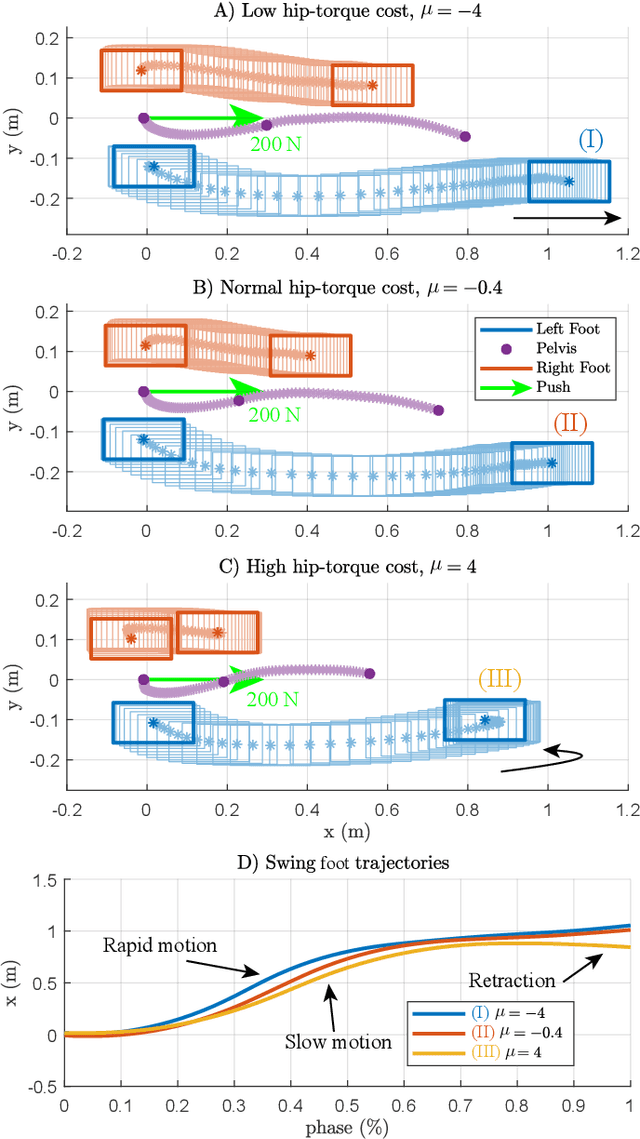
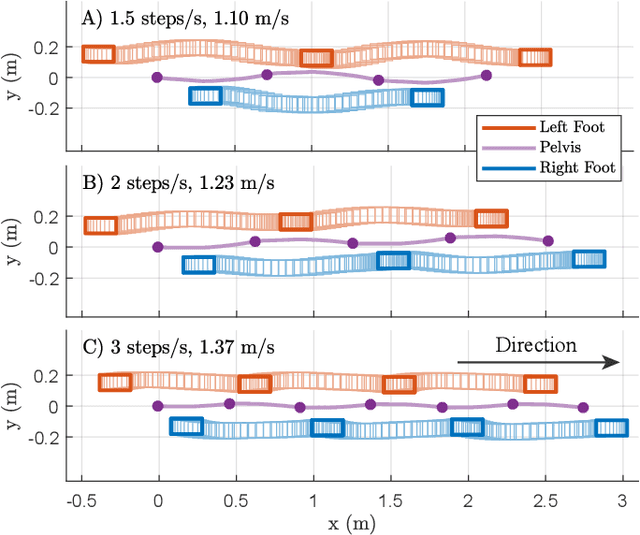
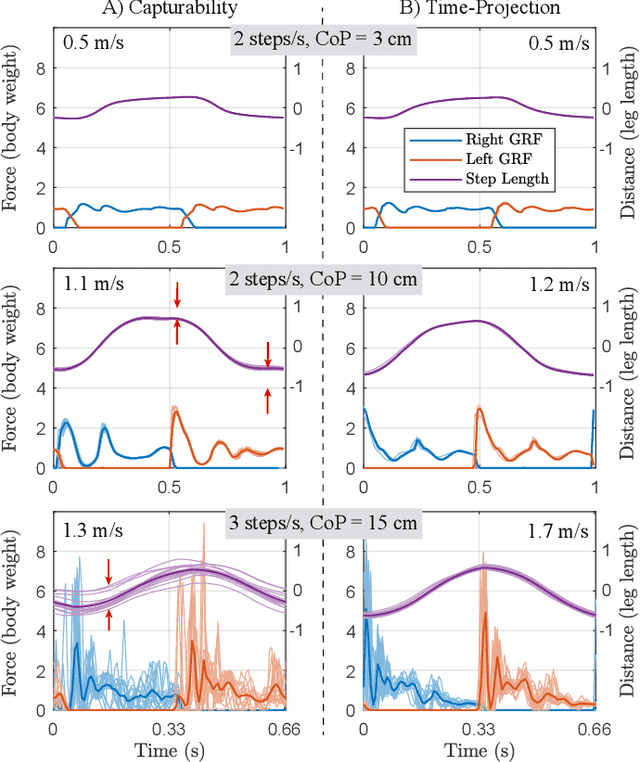
We present a new walking foot-placement controller based on 3LP, a 3D model of bipedal walking that is composed of three pendulums to simulate falling, swing and torso dynamics. Taking advantage of linear equations and closed-form solutions of the 3LP model, our proposed controller projects intermediate states of the biped back to the beginning of the phase for which a discrete LQR controller is designed. After the projection, a proper control policy is generated by this LQR controller and used at the intermediate time. This control paradigm reacts to disturbances immediately and includes rules to account for swing dynamics and leg-retraction. We apply it to a simulated Atlas robot in position-control, always commanded to perform in-place walking. The stance hip joint in our robot keeps the torso upright to let the robot naturally fall, and the swing hip joint tracks the desired footstep location. Combined with simple Center of Pressure (CoP) damping rules in the low-level controller, our foot-placement enables the robot to recover from strong pushes and produce periodic walking gaits when subject to persistent sources of disturbance, externally or internally. These gaits are imprecise, i.e., emergent from asymmetry sources rather than precisely imposing a desired velocity to the robot. Also in extreme conditions, restricting linearity assumptions of the 3LP model are often violated, but the system remains robust in our simulations. An extensive analysis of closed-loop eigenvalues, viable regions and sensitivity to push timings further demonstrate the strengths of our simple controller.

Time-projection control to recover inter-sample disturbances, application to bipedal walking control

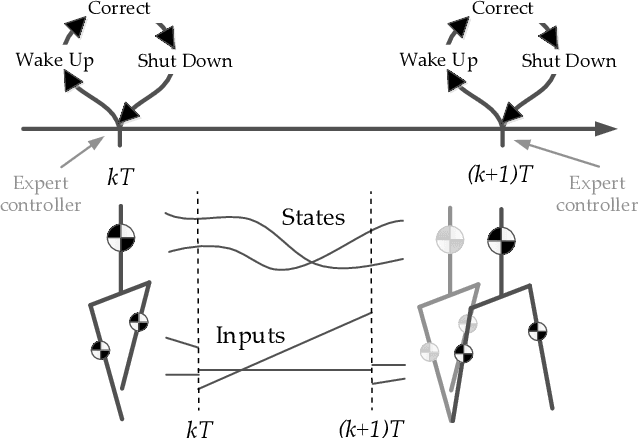
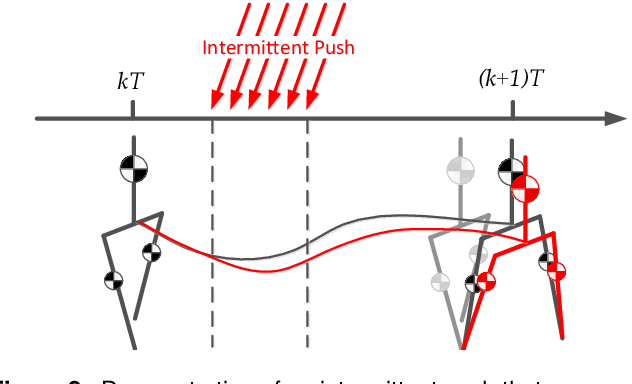
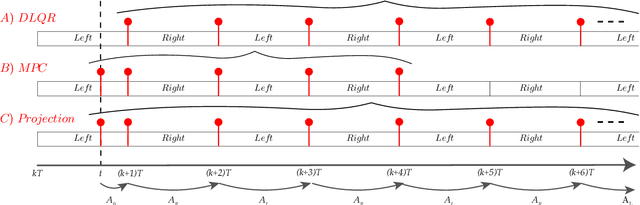
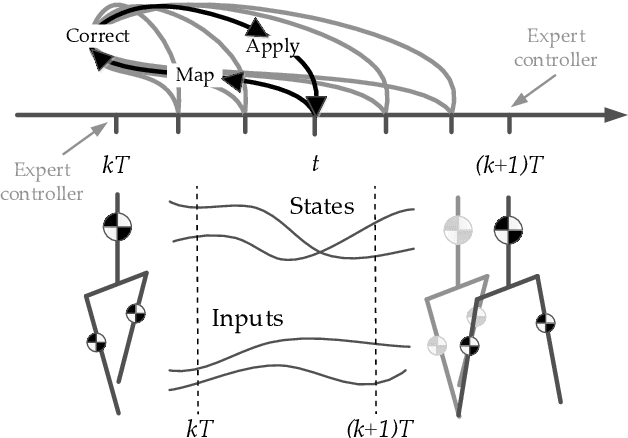
We present a new walking controller based on 3LP, a 3D model of bipedal walking that is composed of three pendulums to simulate falling, swing and torso dynamics. Taking advantage of linear equations and closed-form solutions of 3LP, the proposed controller projects intermediate states of the biped back to the beginning of the phase for which a discrete LQR controller is designed. After the projection, a proper control policy is generated by this LQR controller and used at the intermediate time. The projection controller reacts to disturbances immediately and compared to the discrete LQR controller, it provides superior performance in recovering intermittent external pushes. Further analysis of closed-loop eigenvalues and disturbance rejection strength show strong stabilization properties for this architecture. An analysis of viable regions also show that the proposed controller covers most of the maximal viable set of states. It is computationally much faster than Model Predictive Controllers (MPC) and yet optimal over an infinite horizon.