Fast L1-Minimization Algorithms For Robust Face Recognition

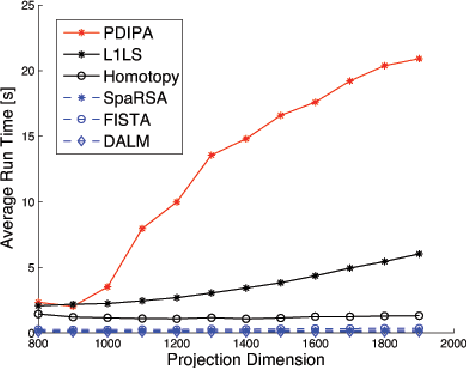
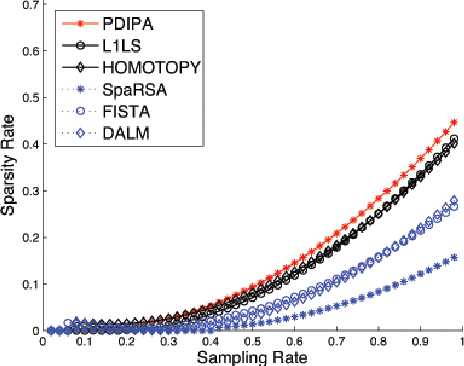
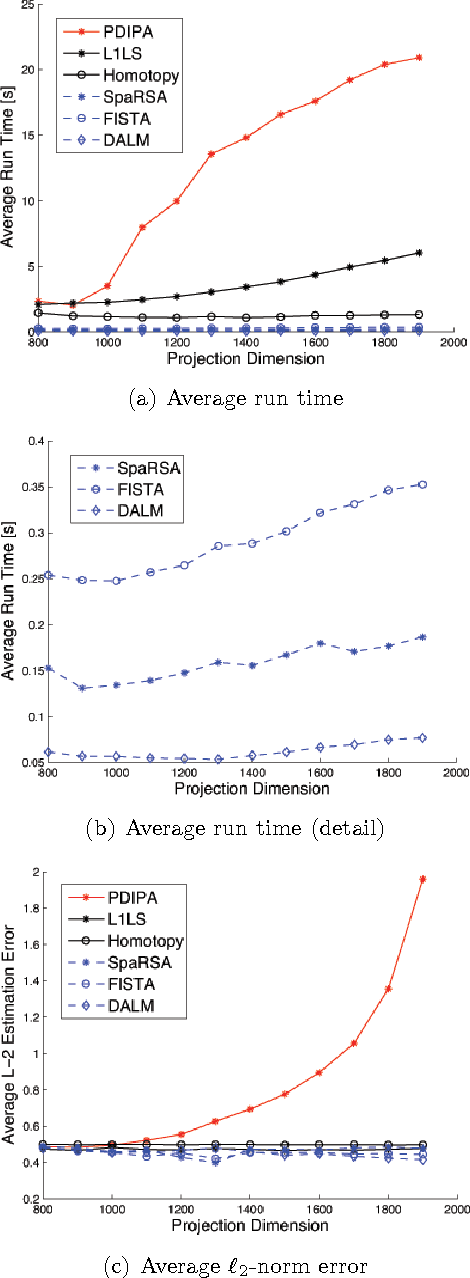
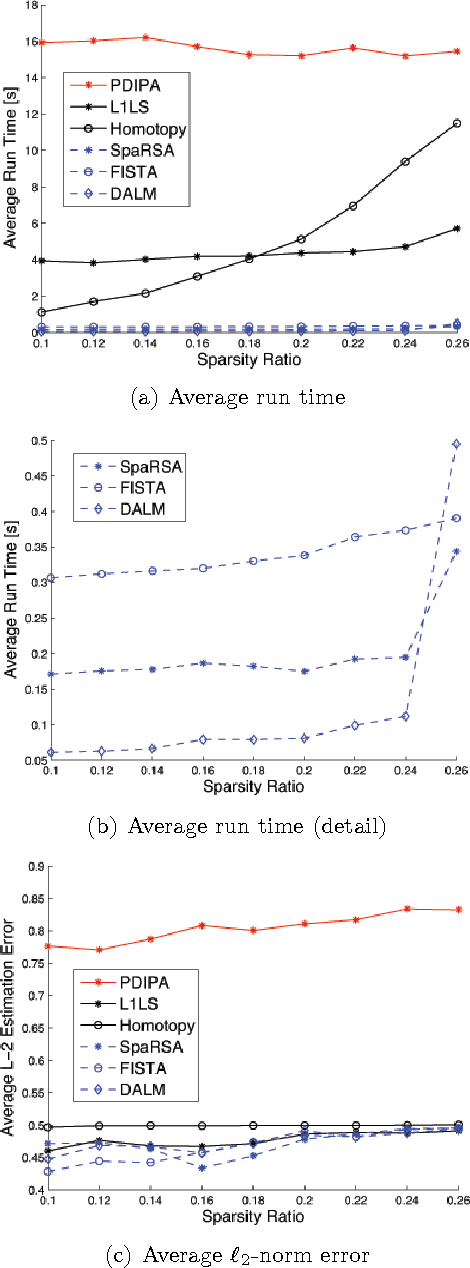
L1-minimization refers to finding the minimum L1-norm solution to an underdetermined linear system b=Ax. Under certain conditions as described in compressive sensing theory, the minimum L1-norm solution is also the sparsest solution. In this paper, our study addresses the speed and scalability of its algorithms. In particular, we focus on the numerical implementation of a sparsity-based classification framework in robust face recognition, where sparse representation is sought to recover human identities from very high-dimensional facial images that may be corrupted by illumination, facial disguise, and pose variation. Although the underlying numerical problem is a linear program, traditional algorithms are known to suffer poor scalability for large-scale applications. We investigate a new solution based on a classical convex optimization framework, known as Augmented Lagrangian Methods (ALM). The new convex solvers provide a viable solution to real-world, time-critical applications such as face recognition. We conduct extensive experiments to validate and compare the performance of the ALM algorithms against several popular L1-minimization solvers, including interior-point method, Homotopy, FISTA, SESOP-PCD, approximate message passing (AMP) and TFOCS. To aid peer evaluation, the code for all the algorithms has been made publicly available.

Sparsity and Robustness in Face Recognition

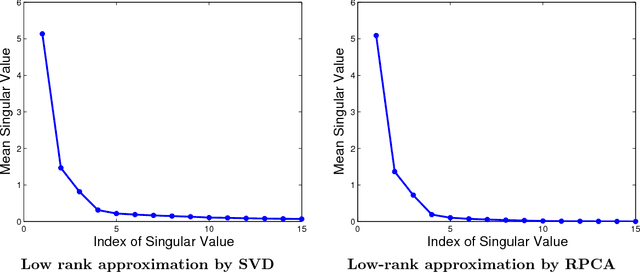
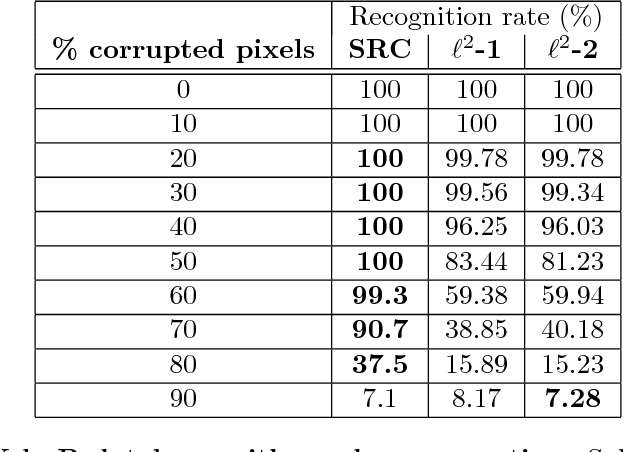
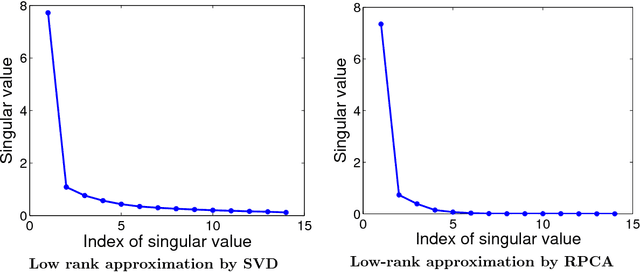
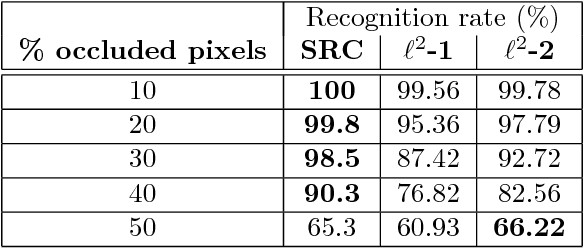
This report concerns the use of techniques for sparse signal representation and sparse error correction for automatic face recognition. Much of the recent interest in these techniques comes from the paper "Robust Face Recognition via Sparse Representation" by Wright et al. (2009), which showed how, under certain technical conditions, one could cast the face recognition problem as one of seeking a sparse representation of a given input face image in terms of a "dictionary" of training images and images of individual pixels. In this report, we have attempted to clarify some frequently encountered questions about this work and particularly, on the validity of using sparse representation techniques for face recognition.

TILT: Transform Invariant Low-rank Textures

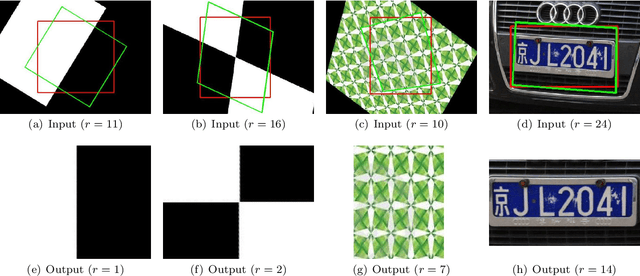
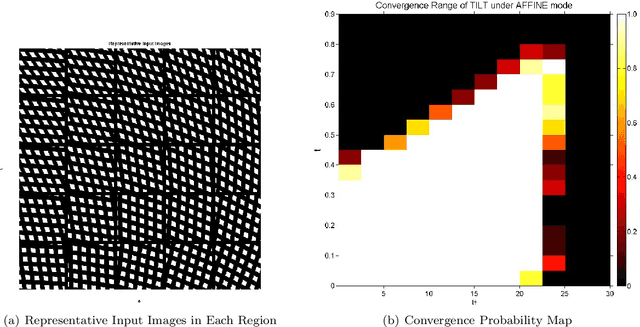
In this paper, we show how to efficiently and effectively extract a class of "low-rank textures" in a 3D scene from 2D images despite significant corruptions and warping. The low-rank textures capture geometrically meaningful structures in an image, which encompass conventional local features such as edges and corners as well as all kinds of regular, symmetric patterns ubiquitous in urban environments and man-made objects. Our approach to finding these low-rank textures leverages the recent breakthroughs in convex optimization that enable robust recovery of a high-dimensional low-rank matrix despite gross sparse errors. In the case of planar regions with significant affine or projective deformation, our method can accurately recover both the intrinsic low-rank texture and the precise domain transformation, and hence the 3D geometry and appearance of the planar regions. Extensive experimental results demonstrate that this new technique works effectively for many regular and near-regular patterns or objects that are approximately low-rank, such as symmetrical patterns, building facades, printed texts, and human faces.