Fast L1-Minimization Algorithms For Robust Face Recognition
Paper and Code
Aug 26, 2012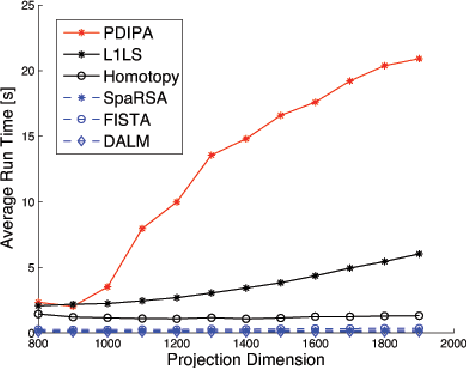
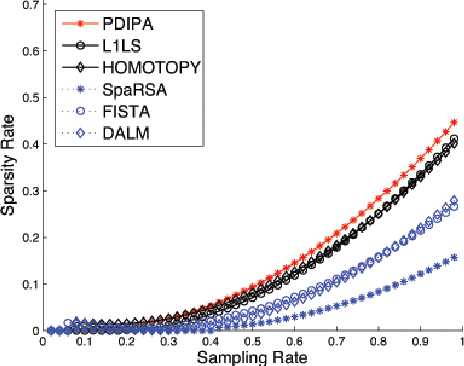
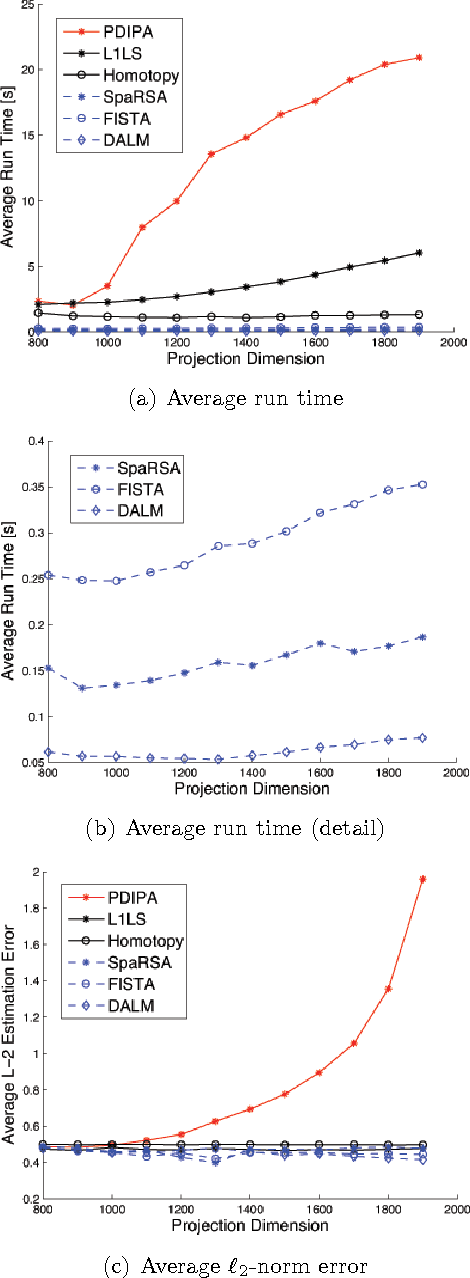
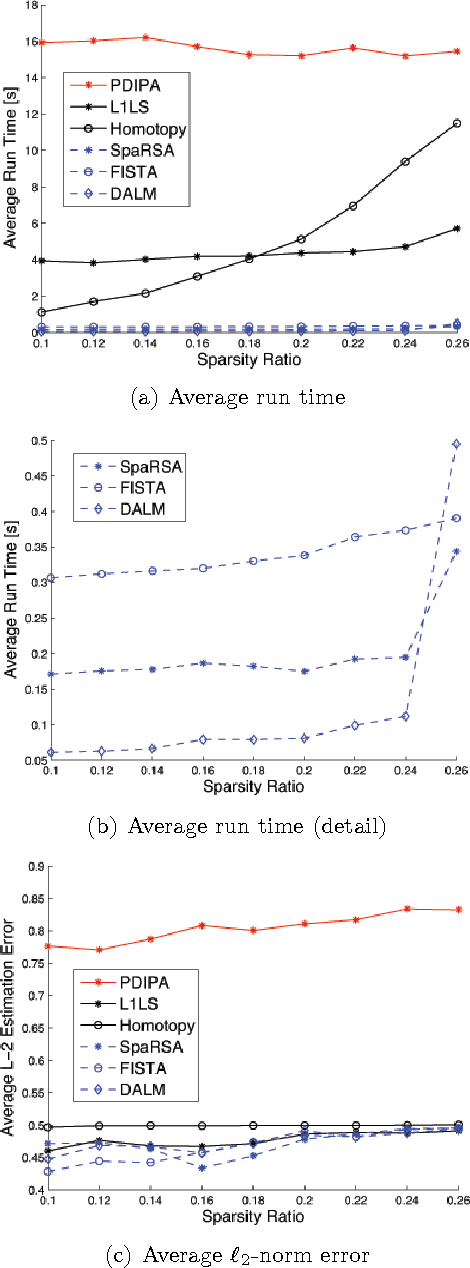
L1-minimization refers to finding the minimum L1-norm solution to an underdetermined linear system b=Ax. Under certain conditions as described in compressive sensing theory, the minimum L1-norm solution is also the sparsest solution. In this paper, our study addresses the speed and scalability of its algorithms. In particular, we focus on the numerical implementation of a sparsity-based classification framework in robust face recognition, where sparse representation is sought to recover human identities from very high-dimensional facial images that may be corrupted by illumination, facial disguise, and pose variation. Although the underlying numerical problem is a linear program, traditional algorithms are known to suffer poor scalability for large-scale applications. We investigate a new solution based on a classical convex optimization framework, known as Augmented Lagrangian Methods (ALM). The new convex solvers provide a viable solution to real-world, time-critical applications such as face recognition. We conduct extensive experiments to validate and compare the performance of the ALM algorithms against several popular L1-minimization solvers, including interior-point method, Homotopy, FISTA, SESOP-PCD, approximate message passing (AMP) and TFOCS. To aid peer evaluation, the code for all the algorithms has been made publicly available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge