Functional Generalized Canonical Correlation Analysis for studying multiple longitudinal variables

In this paper, we introduce Functional Generalized Canonical Correlation Analysis (FGCCA), a new framework for exploring associations between multiple random processes observed jointly. The framework is based on the multiblock Regularized Generalized Canonical Correlation Analysis (RGCCA) framework. It is robust to sparsely and irregularly observed data, making it applicable in many settings. We establish the monotonic property of the solving procedure and introduce a Bayesian approach for estimating canonical components. We propose an extension of the framework that allows the integration of a univariate or multivariate response into the analysis, paving the way for predictive applications. We evaluate the method's efficiency in simulation studies and present a use case on a longitudinal dataset.

Tensor Generalized Canonical Correlation Analysis

Regularized Generalized Canonical Correlation Analysis (RGCCA) is a general statistical framework for multi-block data analysis. RGCCA enables deciphering relationships between several sets of variables and subsumes many well-known multivariate analysis methods as special cases. However, RGCCA only deals with vector-valued blocks, disregarding their possible higher-order structures. This paper presents Tensor GCCA (TGCCA), a new method for analyzing higher-order tensors with canonical vectors admitting an orthogonal rank-R CP decomposition. Moreover, two algorithms for TGCCA, based on whether a separable covariance structure is imposed or not, are presented along with convergence guarantees. The efficiency and usefulness of TGCCA are evaluated on simulated and real data and compared favorably to state-of-the-art approaches.

Fast Non-Parametric Tests of Relative Dependency and Similarity

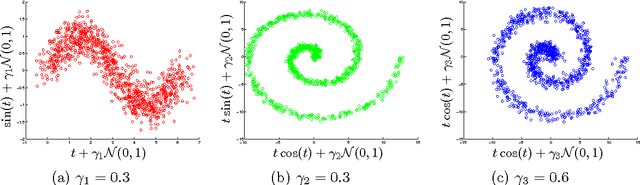
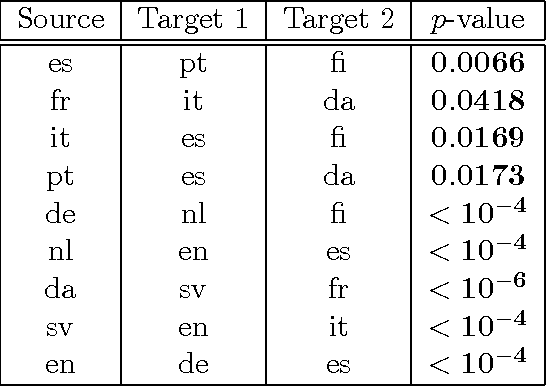
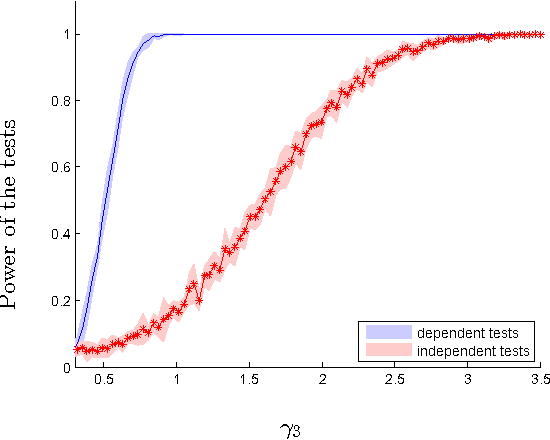
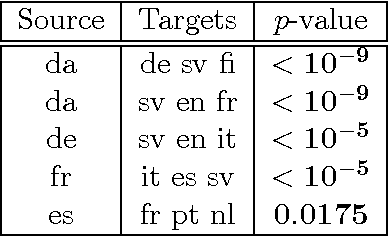
We introduce two novel non-parametric statistical hypothesis tests. The first test, called the relative test of dependency, enables us to determine whether one source variable is significantly more dependent on a first target variable or a second. Dependence is measured via the Hilbert-Schmidt Independence Criterion (HSIC). The second test, called the relative test of similarity, is use to determine which of the two samples from arbitrary distributions is significantly closer to a reference sample of interest and the relative measure of similarity is based on the Maximum Mean Discrepancy (MMD). To construct these tests, we have used as our test statistics the difference of HSIC statistics and of MMD statistics, respectively. The resulting tests are consistent and unbiased, and have favorable convergence properties. The effectiveness of the relative dependency test is demonstrated on several real-world problems: we identify languages groups from a multilingual parallel corpus, and we show that tumor location is more dependent on gene expression than chromosome imbalance. We also demonstrate the performance of the relative test of similarity over a broad selection of model comparisons problems in deep generative models.

A general multiblock method for structured variable selection

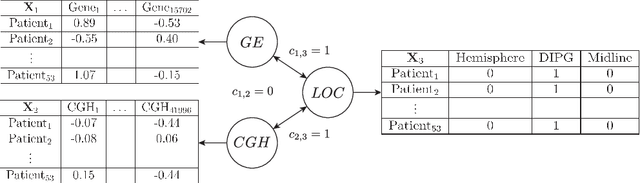
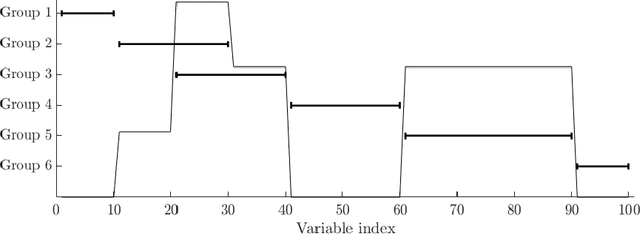
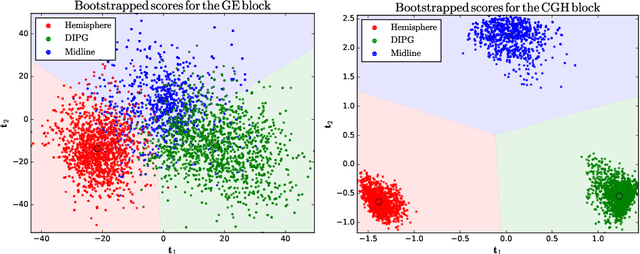
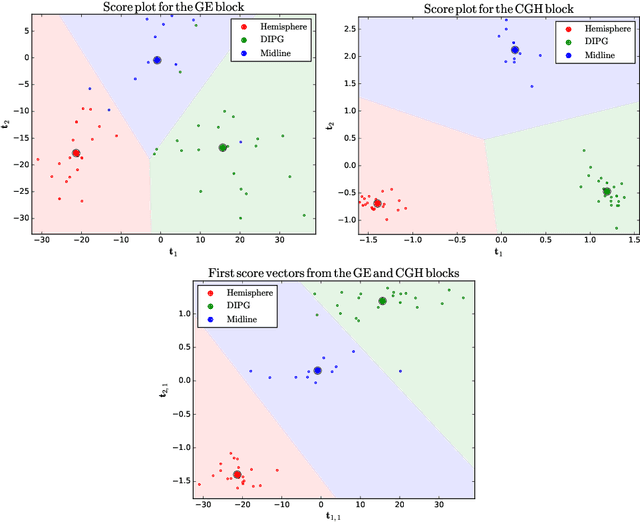
Regularised canonical correlation analysis was recently extended to more than two sets of variables by the multiblock method Regularised generalised canonical correlation analysis (RGCCA). Further, Sparse GCCA (SGCCA) was proposed to address the issue of variable selection. However, for technical reasons, the variable selection offered by SGCCA was restricted to a covariance link between the blocks (i.e., with $\tau=1$). One of the main contributions of this paper is to go beyond the covariance link and to propose an extension of SGCCA for the full RGCCA model (i.e., with $\tau\in[0, 1]$). In addition, we propose an extension of SGCCA that exploits structural relationships between variables within blocks. Specifically, we propose an algorithm that allows structured and sparsity-inducing penalties to be included in the RGCCA optimisation problem. The proposed multiblock method is illustrated on a real three-block high-grade glioma data set, where the aim is to predict the location of the brain tumours, and on a simulated data set, where the aim is to illustrate the method's ability to reconstruct the true underlying weight vectors.

A low variance consistent test of relative dependency

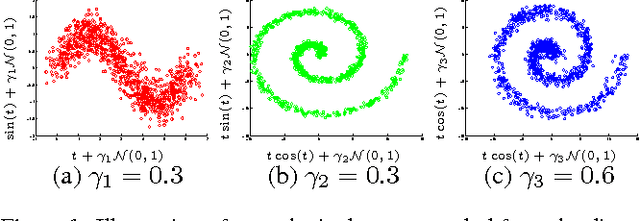
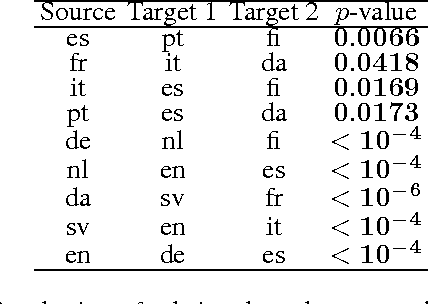
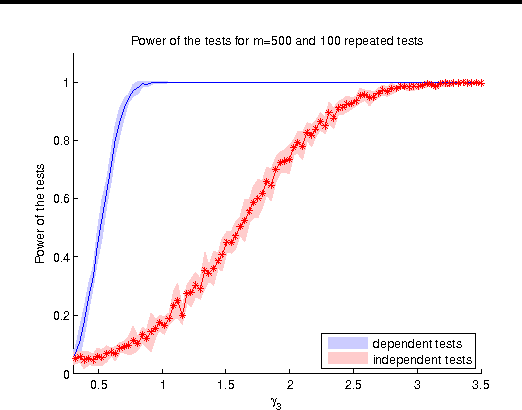
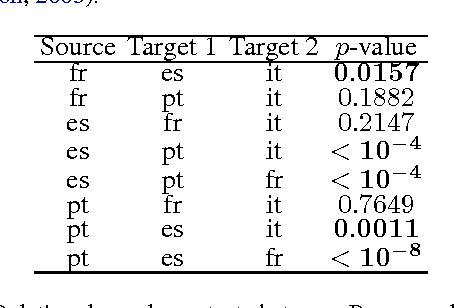
We describe a novel non-parametric statistical hypothesis test of relative dependence between a source variable and two candidate target variables. Such a test enables us to determine whether one source variable is significantly more dependent on a first target variable or a second. Dependence is measured via the Hilbert-Schmidt Independence Criterion (HSIC), resulting in a pair of empirical dependence measures (source-target 1, source-target 2). We test whether the first dependence measure is significantly larger than the second. Modeling the covariance between these HSIC statistics leads to a provably more powerful test than the construction of independent HSIC statistics by sub-sampling. The resulting test is consistent and unbiased, and (being based on U-statistics) has favorable convergence properties. The test can be computed in quadratic time, matching the computational complexity of standard empirical HSIC estimators. The effectiveness of the test is demonstrated on several real-world problems: we identify language groups from a multilingual corpus, and we prove that tumor location is more dependent on gene expression than chromosomal imbalances. Source code is available for download at https://github.com/wbounliphone/reldep.