Continuation of Nesterov's Smoothing for Regression with Structured Sparsity in High-Dimensional Neuroimaging

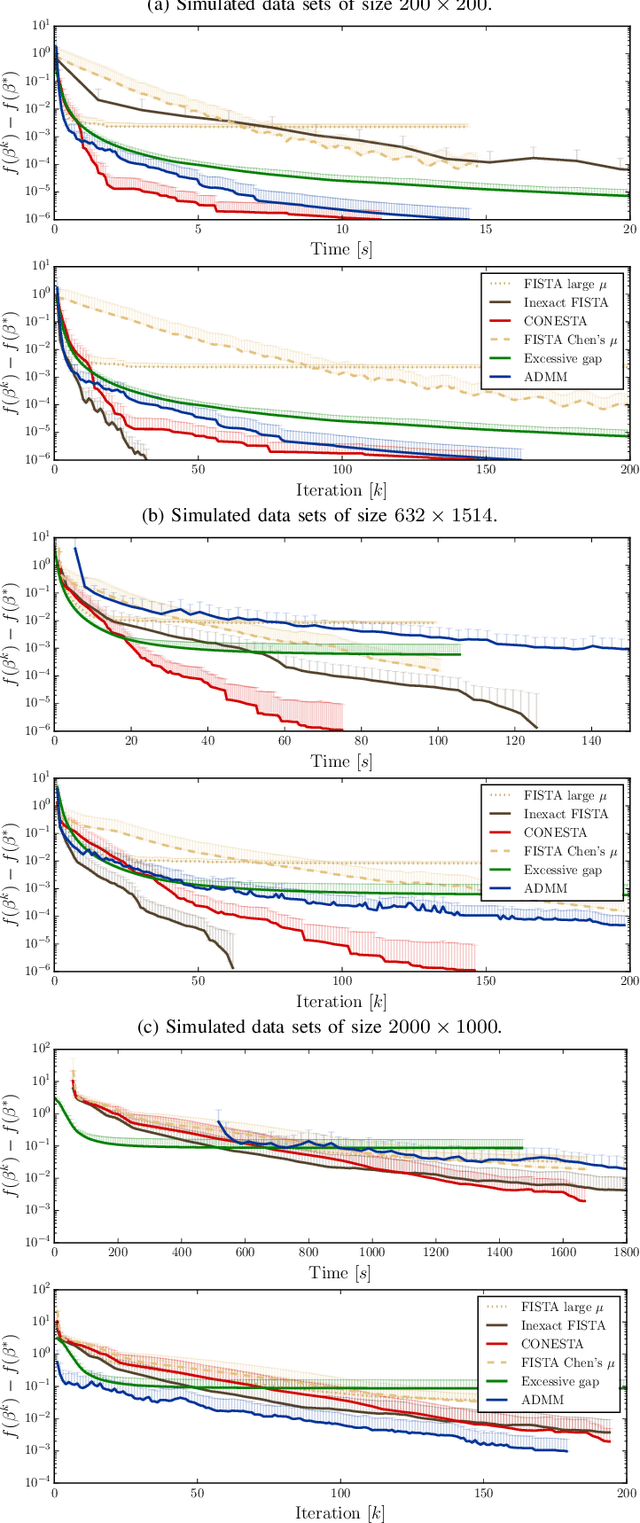
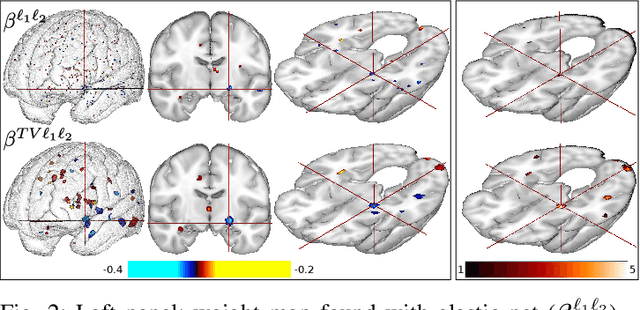
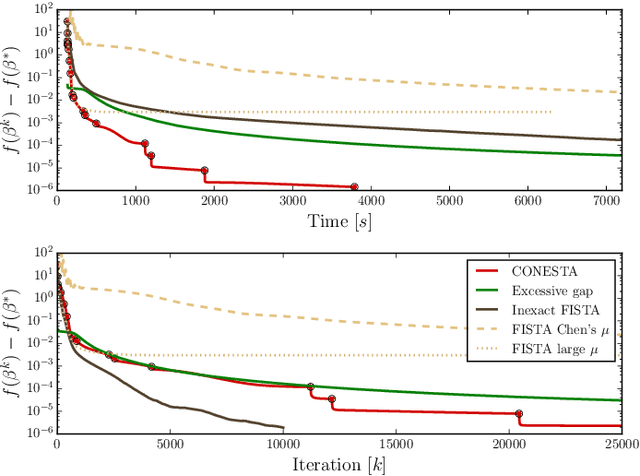
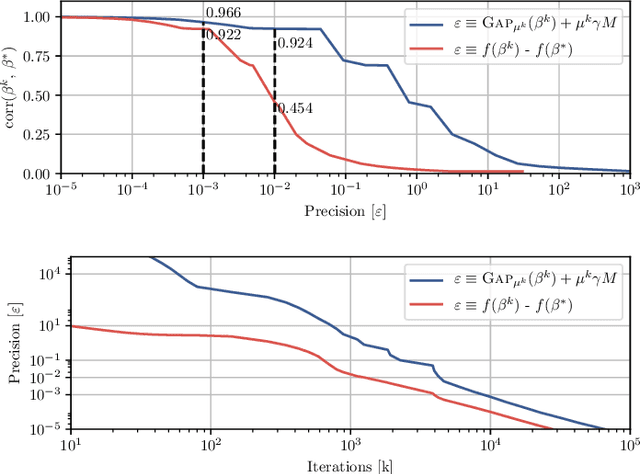
Predictive models can be used on high-dimensional brain images for diagnosis of a clinical condition. Spatial regularization through structured sparsity offers new perspectives in this context and reduces the risk of overfitting the model while providing interpretable neuroimaging signatures by forcing the solution to adhere to domain-specific constraints. Total Variation (TV) enforces spatial smoothness of the solution while segmenting predictive regions from the background. We consider the problem of minimizing the sum of a smooth convex loss, a non-smooth convex penalty (whose proximal operator is known) and a wide range of possible complex, non-smooth convex structured penalties such as TV or overlapping group Lasso. Existing solvers are either limited in the functions they can minimize or in their practical capacity to scale to high-dimensional imaging data. Nesterov's smoothing technique can be used to minimize a large number of non-smooth convex structured penalties but reasonable precision requires a small smoothing parameter, which slows down the convergence speed. To benefit from the versatility of Nesterov's smoothing technique, we propose a first order continuation algorithm, CONESTA, which automatically generates a sequence of decreasing smoothing parameters. The generated sequence maintains the optimal convergence speed towards any globally desired precision. Our main contributions are: To propose an expression of the duality gap to probe the current distance to the global optimum in order to adapt the smoothing parameter and the convergence speed. We provide a convergence rate, which is an improvement over classical proximal gradient smoothing methods. We demonstrate on both simulated and high-dimensional structural neuroimaging data that CONESTA significantly outperforms many state-of-the-art solvers in regard to convergence speed and precision.

A general multiblock method for structured variable selection

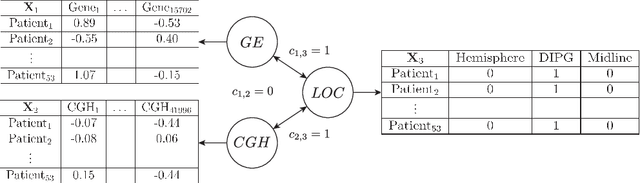
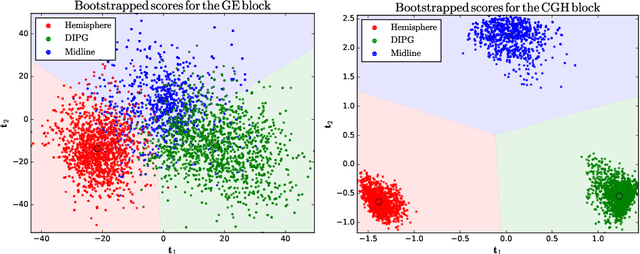
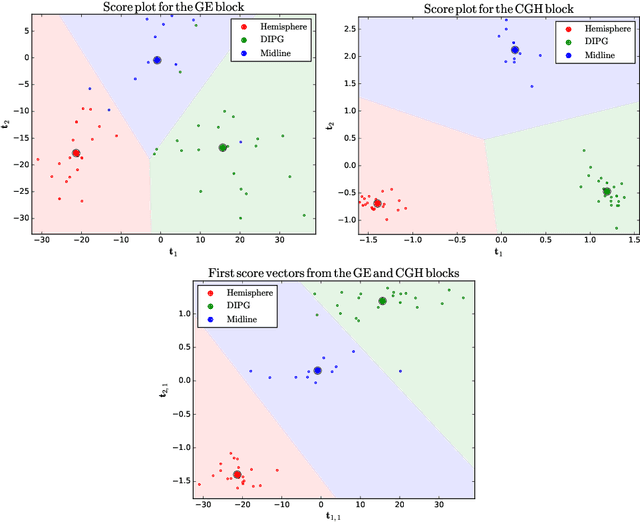
Regularised canonical correlation analysis was recently extended to more than two sets of variables by the multiblock method Regularised generalised canonical correlation analysis (RGCCA). Further, Sparse GCCA (SGCCA) was proposed to address the issue of variable selection. However, for technical reasons, the variable selection offered by SGCCA was restricted to a covariance link between the blocks (i.e., with $\tau=1$). One of the main contributions of this paper is to go beyond the covariance link and to propose an extension of SGCCA for the full RGCCA model (i.e., with $\tau\in[0, 1]$). In addition, we propose an extension of SGCCA that exploits structural relationships between variables within blocks. Specifically, we propose an algorithm that allows structured and sparsity-inducing penalties to be included in the RGCCA optimisation problem. The proposed multiblock method is illustrated on a real three-block high-grade glioma data set, where the aim is to predict the location of the brain tumours, and on a simulated data set, where the aim is to illustrate the method's ability to reconstruct the true underlying weight vectors.