Continuation of Nesterov's Smoothing for Regression with Structured Sparsity in High-Dimensional Neuroimaging

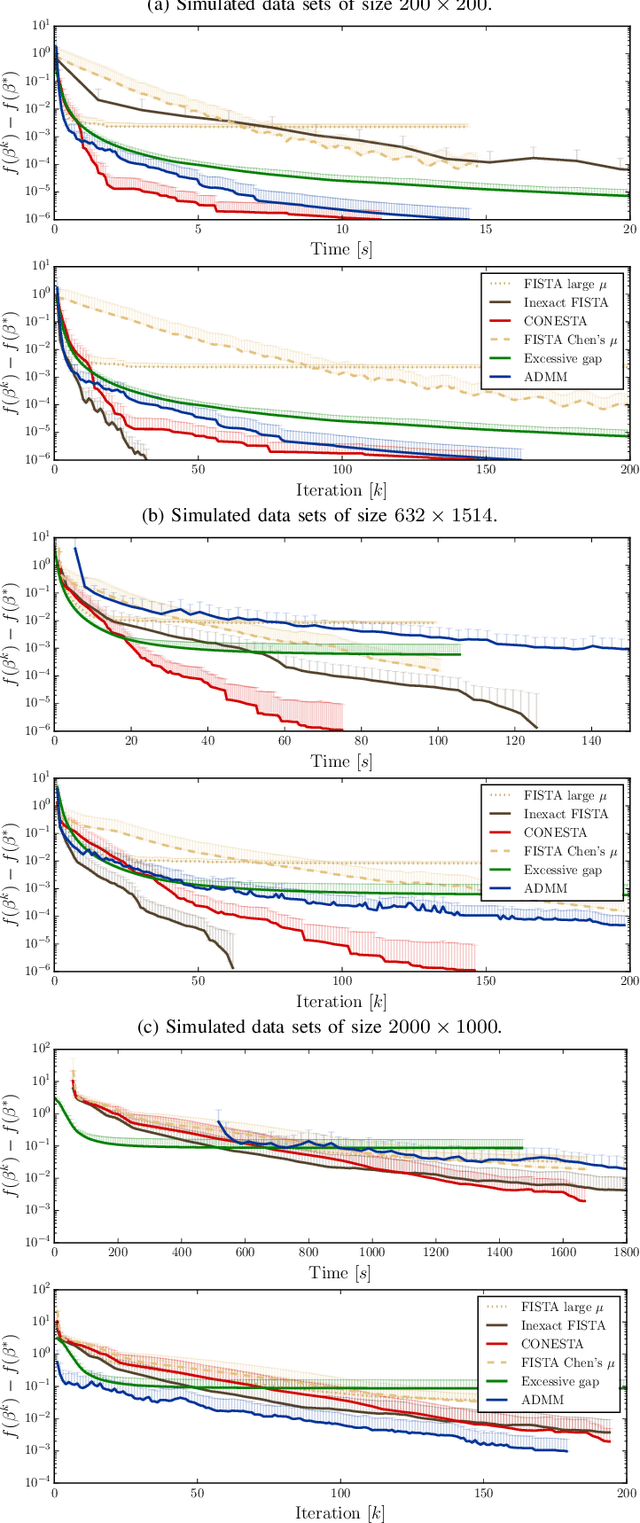
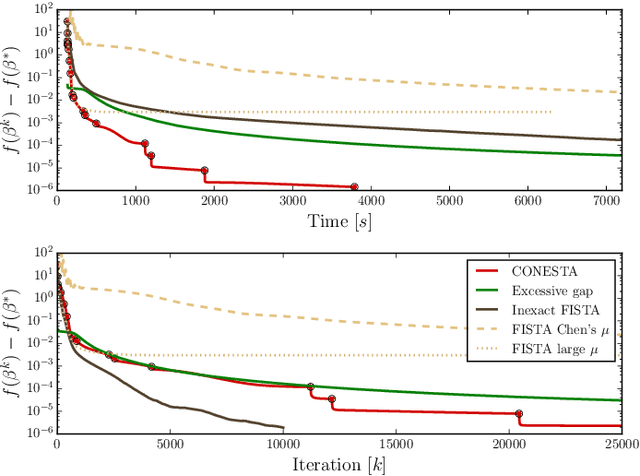
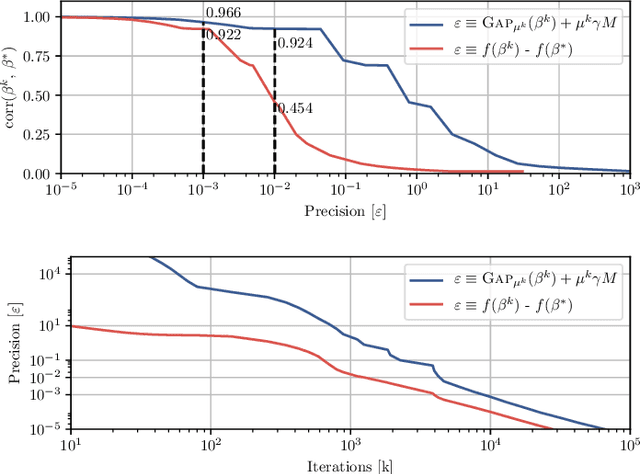
Predictive models can be used on high-dimensional brain images for diagnosis of a clinical condition. Spatial regularization through structured sparsity offers new perspectives in this context and reduces the risk of overfitting the model while providing interpretable neuroimaging signatures by forcing the solution to adhere to domain-specific constraints. Total Variation (TV) enforces spatial smoothness of the solution while segmenting predictive regions from the background. We consider the problem of minimizing the sum of a smooth convex loss, a non-smooth convex penalty (whose proximal operator is known) and a wide range of possible complex, non-smooth convex structured penalties such as TV or overlapping group Lasso. Existing solvers are either limited in the functions they can minimize or in their practical capacity to scale to high-dimensional imaging data. Nesterov's smoothing technique can be used to minimize a large number of non-smooth convex structured penalties but reasonable precision requires a small smoothing parameter, which slows down the convergence speed. To benefit from the versatility of Nesterov's smoothing technique, we propose a first order continuation algorithm, CONESTA, which automatically generates a sequence of decreasing smoothing parameters. The generated sequence maintains the optimal convergence speed towards any globally desired precision. Our main contributions are: To propose an expression of the duality gap to probe the current distance to the global optimum in order to adapt the smoothing parameter and the convergence speed. We provide a convergence rate, which is an improvement over classical proximal gradient smoothing methods. We demonstrate on both simulated and high-dimensional structural neuroimaging data that CONESTA significantly outperforms many state-of-the-art solvers in regard to convergence speed and precision.

Structured Sparse Principal Components Analysis with the TV-Elastic Net penalty

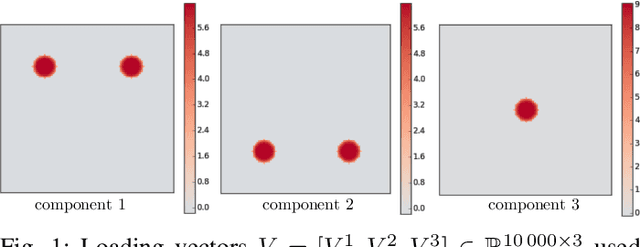
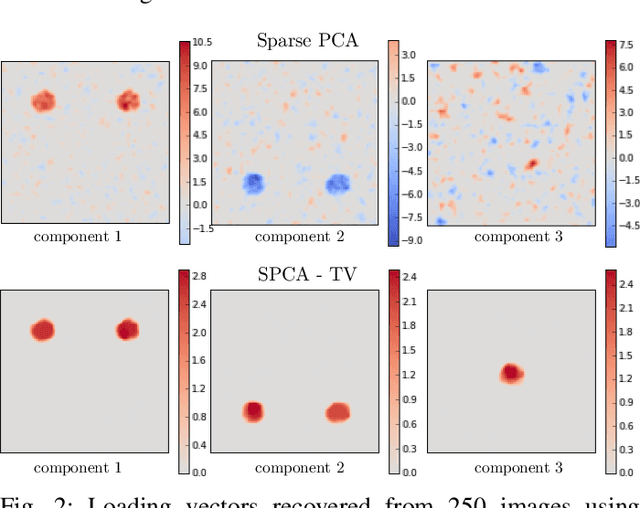
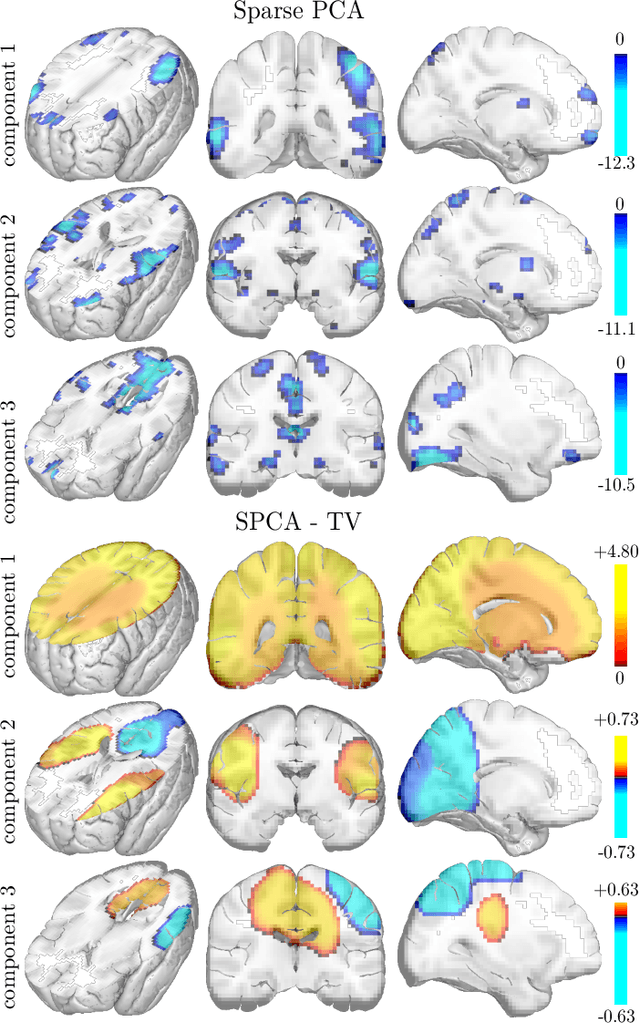
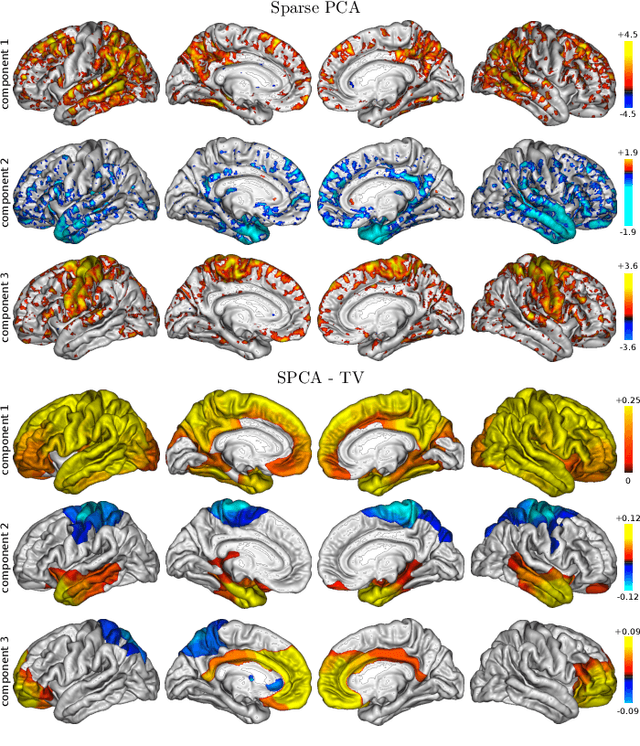
Principal component analysis (PCA) is an exploratory tool widely used in data analysis to uncover dominant patterns of variability within a population. Despite its ability to represent a data set in a low-dimensional space, the interpretability of PCA remains limited. However, in neuroimaging, it is essential to uncover clinically interpretable phenotypic markers that would account for the main variability in the brain images of a population. Recently, some alternatives to the standard PCA approach, such as Sparse PCA, have been proposed, their aim being to limit the density of the components. Nonetheless, sparsity alone does not entirely solve the interpretability problem, since it may yield scattered and unstable components. We hypothesized that the incorporation of prior information regarding the structure of the data may lead to improved relevance and interpretability of brain patterns. We therefore present a simple extension of the popular PCA framework that adds structured sparsity penalties on the loading vectors in order to identify the few stable regions in the brain images accounting for most of the variability. Such structured sparsity can be obtained by combining l1 and total variation (TV) penalties, where the TV regularization encodes higher order information about the structure of the data. This paper presents the structured sparse PCA (denoted SPCA-TV) optimization framework and its resolution. We demonstrate the efficiency and versatility of SPCA-TV on three different data sets. The gains of SPCA-TV over unstructured approaches are significant,since SPCA-TV reveals the variability within a data set in the form of intelligible brain patterns that are easy to interpret, and are more stable across different samples.

Predictive support recovery with TV-Elastic Net penalty and logistic regression: an application to structural MRI

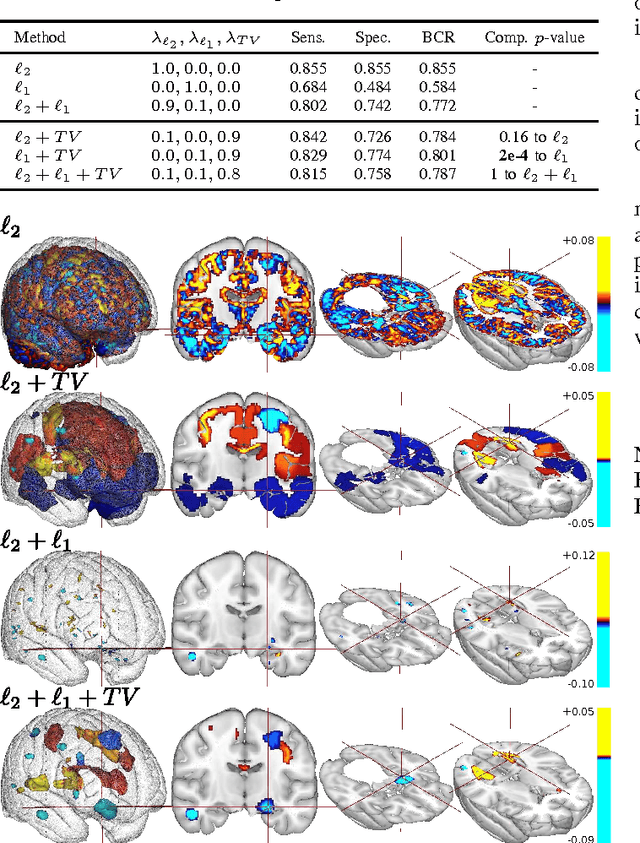
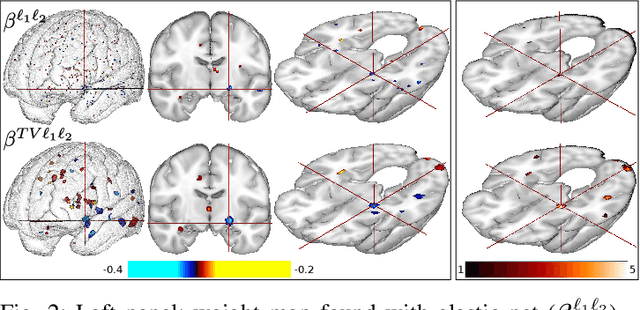
The use of machine-learning in neuroimaging offers new perspectives in early diagnosis and prognosis of brain diseases. Although such multivariate methods can capture complex relationships in the data, traditional approaches provide irregular (l2 penalty) or scattered (l1 penalty) predictive pattern with a very limited relevance. A penalty like Total Variation (TV) that exploits the natural 3D structure of the images can increase the spatial coherence of the weight map. However, TV penalization leads to non-smooth optimization problems that are hard to minimize. We propose an optimization framework that minimizes any combination of l1, l2, and TV penalties while preserving the exact l1 penalty. This algorithm uses Nesterov's smoothing technique to approximate the TV penalty with a smooth function such that the loss and the penalties are minimized with an exact accelerated proximal gradient algorithm. We propose an original continuation algorithm that uses successively smaller values of the smoothing parameter to reach a prescribed precision while achieving the best possible convergence rate. This algorithm can be used with other losses or penalties. The algorithm is applied on a classification problem on the ADNI dataset. We observe that the TV penalty does not necessarily improve the prediction but provides a major breakthrough in terms of support recovery of the predictive brain regions.

Using n-grams models for visual semantic place recognition

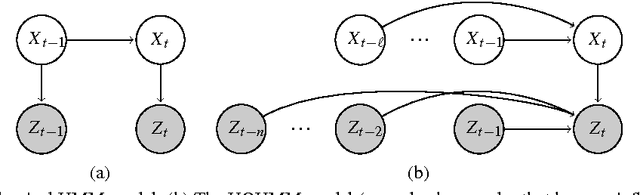
The aim of this paper is to present a new method for visual place recognition. Our system combines global image characterization and visual words, which allows to use efficient Bayesian filtering methods to integrate several images. More precisely, we extend the classical HMM model with techniques inspired by the field of Natural Language Processing. This paper presents our system and the Bayesian filtering algorithm. The performance of our system and the influence of the main parameters are evaluated on a standard database. The discussion highlights the interest of using such models and proposes improvements.