Optimizing contrastive learning for cortical folding pattern detection

The human cerebral cortex has many bumps and grooves called gyri and sulci. Even though there is a high inter-individual consistency for the main cortical folds, this is not the case when we examine the exact shapes and details of the folding patterns. Because of this complexity, characterizing the cortical folding variability and relating them to subjects' behavioral characteristics or pathologies is still an open scientific problem. Classical approaches include labeling a few specific patterns, either manually or semi-automatically, based on geometric distances, but the recent availability of MRI image datasets of tens of thousands of subjects makes modern deep-learning techniques particularly attractive. Here, we build a self-supervised deep-learning model to detect folding patterns in the cingulate region. We train a contrastive self-supervised model (SimCLR) on both Human Connectome Project (1101 subjects) and UKBioBank (21070 subjects) datasets with topological-based augmentations on the cortical skeletons, which are topological objects that capture the shape of the folds. We explore several backbone architectures (convolutional network, DenseNet, and PointNet) for the SimCLR. For evaluation and testing, we perform a linear classification task on a database manually labeled for the presence of the "double-parallel" folding pattern in the cingulate region, which is related to schizophrenia characteristics. The best model, giving a test AUC of 0.76, is a convolutional network with 6 layers, a 10-dimensional latent space, a linear projection head, and using the branch-clipping augmentation. This is the first time that a self-supervised deep learning model has been applied to cortical skeletons on such a large dataset and quantitatively evaluated. We can now envisage the next step: applying it to other brain regions to detect other biomarkers.

Predictive support recovery with TV-Elastic Net penalty and logistic regression: an application to structural MRI

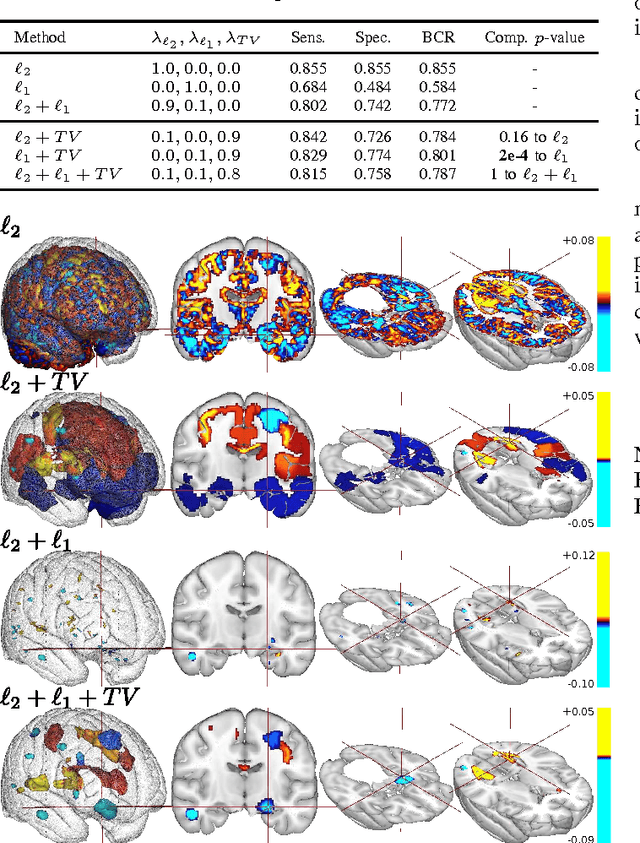
The use of machine-learning in neuroimaging offers new perspectives in early diagnosis and prognosis of brain diseases. Although such multivariate methods can capture complex relationships in the data, traditional approaches provide irregular (l2 penalty) or scattered (l1 penalty) predictive pattern with a very limited relevance. A penalty like Total Variation (TV) that exploits the natural 3D structure of the images can increase the spatial coherence of the weight map. However, TV penalization leads to non-smooth optimization problems that are hard to minimize. We propose an optimization framework that minimizes any combination of l1, l2, and TV penalties while preserving the exact l1 penalty. This algorithm uses Nesterov's smoothing technique to approximate the TV penalty with a smooth function such that the loss and the penalties are minimized with an exact accelerated proximal gradient algorithm. We propose an original continuation algorithm that uses successively smaller values of the smoothing parameter to reach a prescribed precision while achieving the best possible convergence rate. This algorithm can be used with other losses or penalties. The algorithm is applied on a classification problem on the ADNI dataset. We observe that the TV penalty does not necessarily improve the prediction but provides a major breakthrough in terms of support recovery of the predictive brain regions.