Matthew B. Blashcko
Fast Non-Parametric Tests of Relative Dependency and Similarity
Nov 17, 2016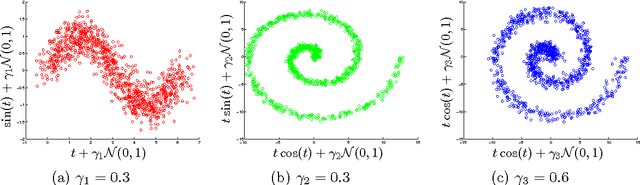
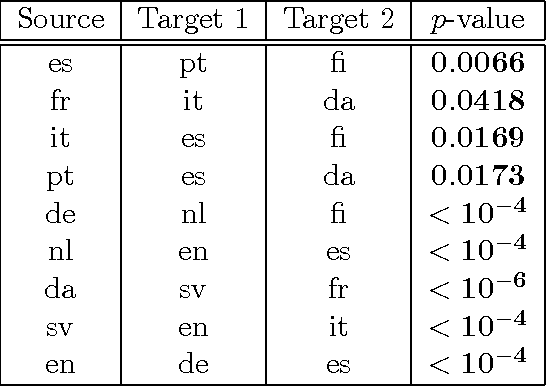
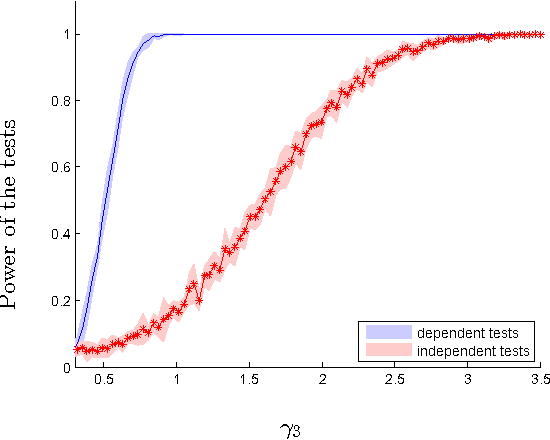
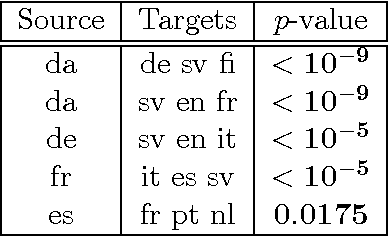
Abstract:We introduce two novel non-parametric statistical hypothesis tests. The first test, called the relative test of dependency, enables us to determine whether one source variable is significantly more dependent on a first target variable or a second. Dependence is measured via the Hilbert-Schmidt Independence Criterion (HSIC). The second test, called the relative test of similarity, is use to determine which of the two samples from arbitrary distributions is significantly closer to a reference sample of interest and the relative measure of similarity is based on the Maximum Mean Discrepancy (MMD). To construct these tests, we have used as our test statistics the difference of HSIC statistics and of MMD statistics, respectively. The resulting tests are consistent and unbiased, and have favorable convergence properties. The effectiveness of the relative dependency test is demonstrated on several real-world problems: we identify languages groups from a multilingual parallel corpus, and we show that tumor location is more dependent on gene expression than chromosome imbalance. We also demonstrate the performance of the relative test of similarity over a broad selection of model comparisons problems in deep generative models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge