Andrea Giovannucci
Deep inference of latent dynamics with spatio-temporal super-resolution using selective backpropagation through time
Oct 29, 2021


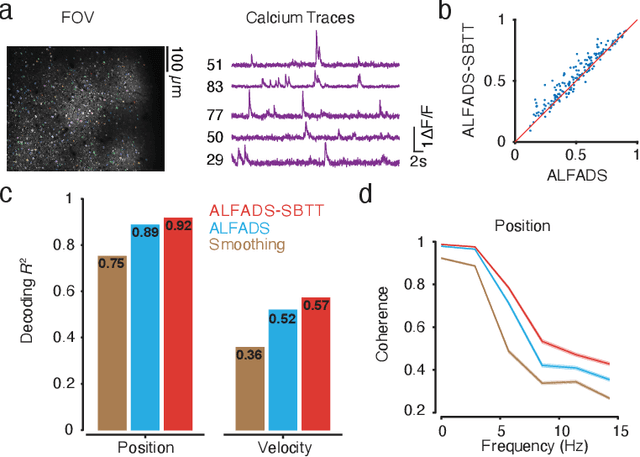
Abstract:Modern neural interfaces allow access to the activity of up to a million neurons within brain circuits. However, bandwidth limits often create a trade-off between greater spatial sampling (more channels or pixels) and the temporal frequency of sampling. Here we demonstrate that it is possible to obtain spatio-temporal super-resolution in neuronal time series by exploiting relationships among neurons, embedded in latent low-dimensional population dynamics. Our novel neural network training strategy, selective backpropagation through time (SBTT), enables learning of deep generative models of latent dynamics from data in which the set of observed variables changes at each time step. The resulting models are able to infer activity for missing samples by combining observations with learned latent dynamics. We test SBTT applied to sequential autoencoders and demonstrate more efficient and higher-fidelity characterization of neural population dynamics in electrophysiological and calcium imaging data. In electrophysiology, SBTT enables accurate inference of neuronal population dynamics with lower interface bandwidths, providing an avenue to significant power savings for implanted neuroelectronic interfaces. In applications to two-photon calcium imaging, SBTT accurately uncovers high-frequency temporal structure underlying neural population activity, substantially outperforming the current state-of-the-art. Finally, we demonstrate that performance could be further improved by using limited, high-bandwidth sampling to pretrain dynamics models, and then using SBTT to adapt these models for sparsely-sampled data.
Efficient Principal Subspace Projection of Streaming Data Through Fast Similarity Matching
Aug 06, 2018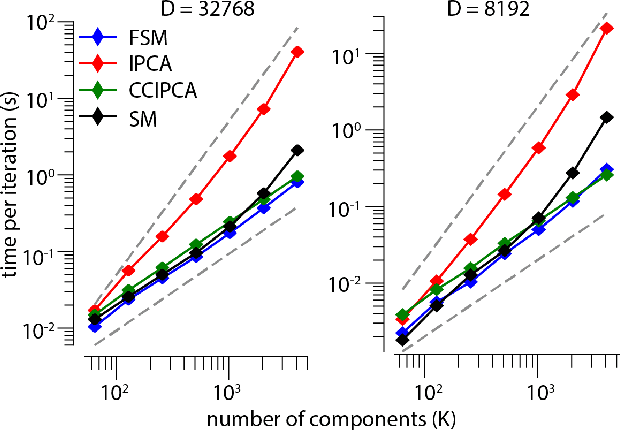
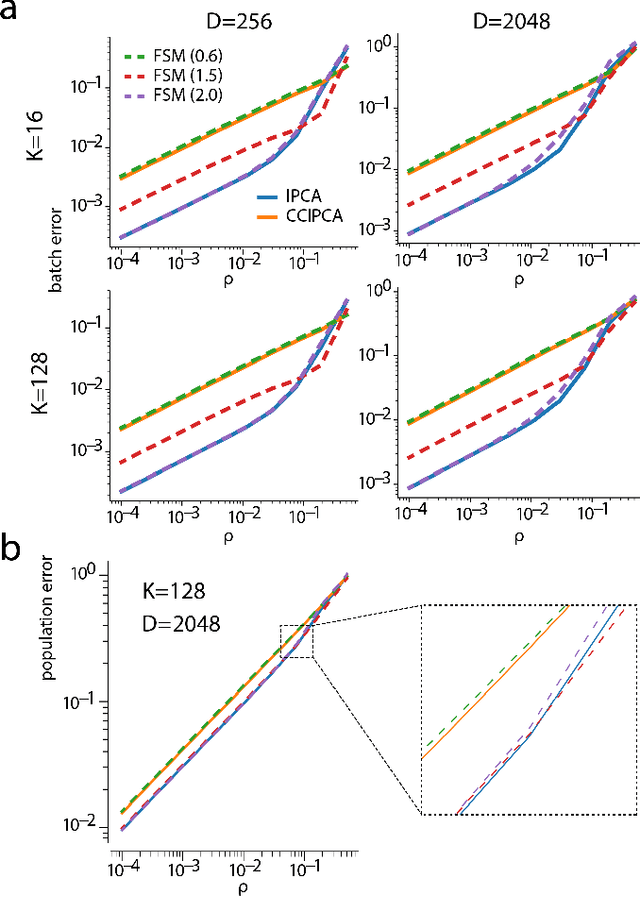
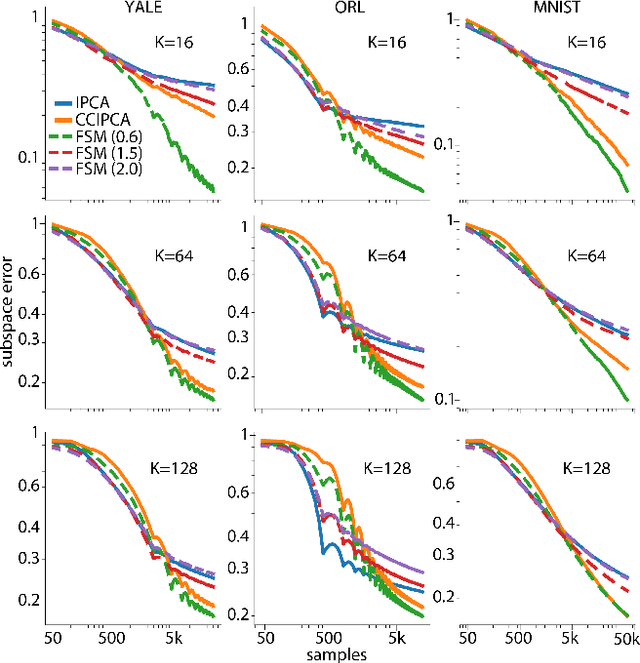
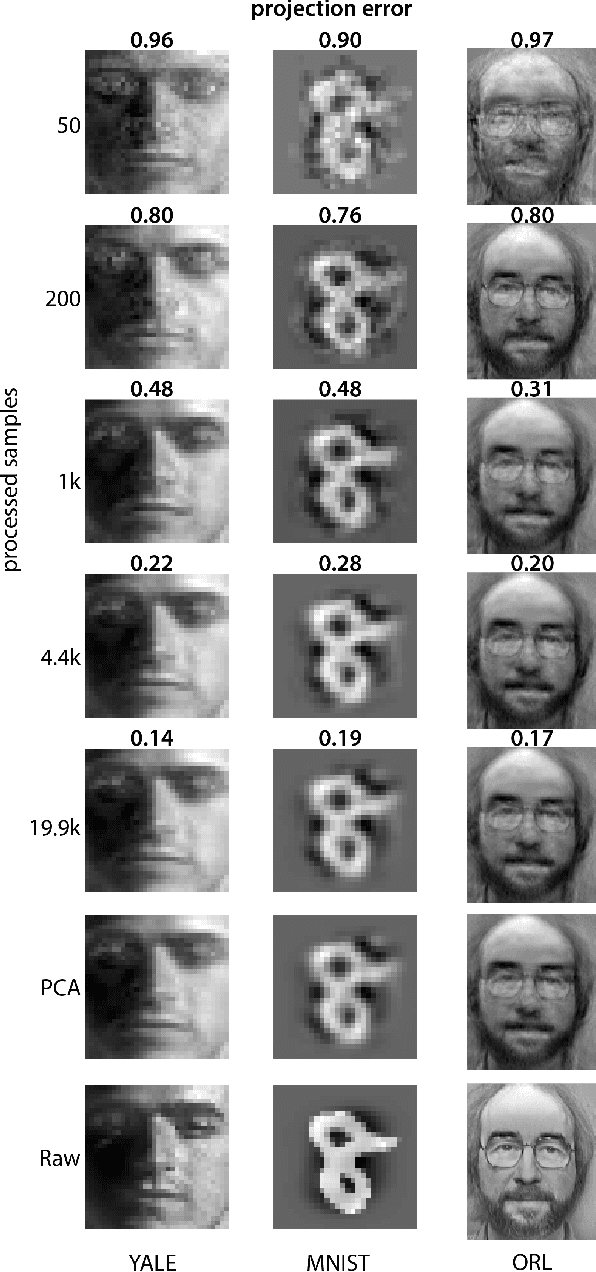
Abstract:Big data problems frequently require processing datasets in a streaming fashion, either because all data are available at once but collectively are larger than available memory or because the data intrinsically arrive one data point at a time and must be processed online. Here, we introduce a computationally efficient version of similarity matching, a framework for online dimensionality reduction that incrementally estimates the top K-dimensional principal subspace of streamed data while keeping in memory only the last sample and the current iterate. To assess the performance of our approach, we construct and make public a test suite containing both a synthetic data generator and the infrastructure to test online dimensionality reduction algorithms on real datasets, as well as performant implementations of our algorithm and competing algorithms with similar aims. Among the algorithms considered we find our approach to be competitive, performing among the best on both synthetic and real data.
An Anytime Algorithm for Optimal Coalition Structure Generation
Jan 15, 2014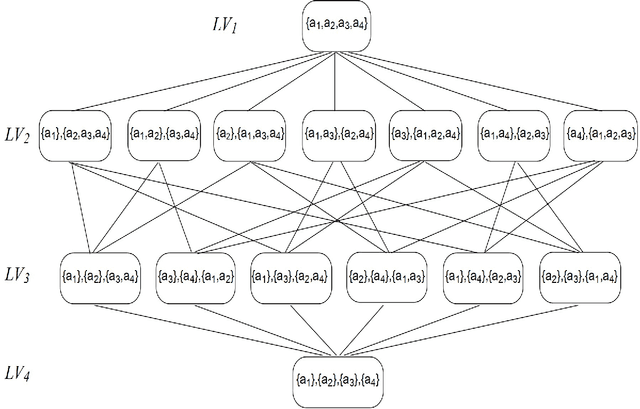
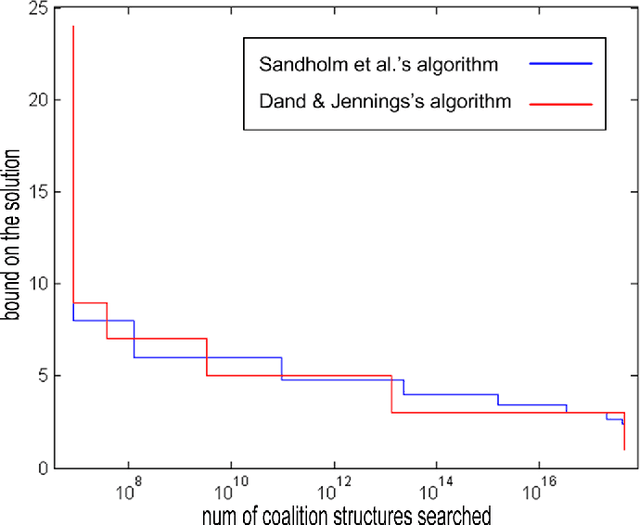
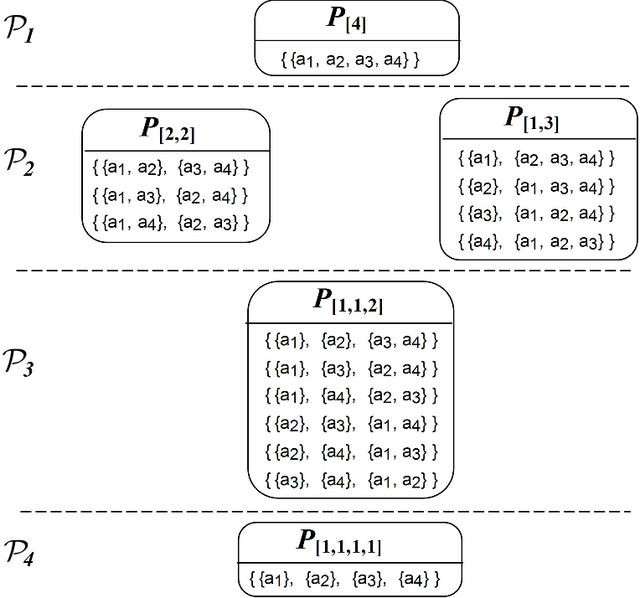
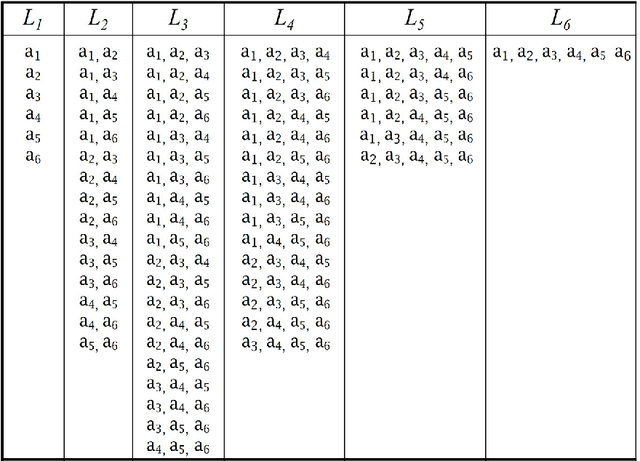
Abstract:Coalition formation is a fundamental type of interaction that involves the creation of coherent groupings of distinct, autonomous, agents in order to efficiently achieve their individual or collective goals. Forming effective coalitions is a major research challenge in the field of multi-agent systems. Central to this endeavour is the problem of determining which of the many possible coalitions to form in order to achieve some goal. This usually requires calculating a value for every possible coalition, known as the coalition value, which indicates how beneficial that coalition would be if it was formed. Once these values are calculated, the agents usually need to find a combination of coalitions, in which every agent belongs to exactly one coalition, and by which the overall outcome of the system is maximized. However, this coalition structure generation problem is extremely challenging due to the number of possible solutions that need to be examined, which grows exponentially with the number of agents involved. To date, therefore, many algorithms have been proposed to solve this problem using different techniques ranging from dynamic programming, to integer programming, to stochastic search all of which suffer from major limitations relating to execution time, solution quality, and memory requirements. With this in mind, we develop an anytime algorithm to solve the coalition structure generation problem. Specifically, the algorithm uses a novel representation of the search space, which partitions the space of possible solutions into sub-spaces such that it is possible to compute upper and lower bounds on the values of the best coalition structures in them. These bounds are then used to identify the sub-spaces that have no potential of containing the optimal solution so that they can be pruned. The algorithm, then, searches through the remaining sub-spaces very efficiently using a branch-and-bound technique to avoid examining all the solutions within the searched subspace(s). In this setting, we prove that our algorithm enumerates all coalition structures efficiently by avoiding redundant and invalid solutions automatically. Moreover, in order to effectively test our algorithm we develop a new type of input distribution which allows us to generate more reliable benchmarks compared to the input distributions previously used in the field. Given this new distribution, we show that for 27 agents our algorithm is able to find solutions that are optimal in 0.175% of the time required by the fastest available algorithm in the literature. The algorithm is anytime, and if interrupted before it would have normally terminated, it can still provide a solution that is guaranteed to be within a bound from the optimal one. Moreover, the guarantees we provide on the quality of the solution are significantly better than those provided by the previous state of the art algorithms designed for this purpose. For example, for the worst case distribution given 25 agents, our algorithm is able to find a 90% efficient solution in around 10% of time it takes to find the optimal solution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge