Joint Audio and Symbolic Conditioning for Temporally Controlled Text-to-Music Generation

We present JASCO, a temporally controlled text-to-music generation model utilizing both symbolic and audio-based conditions. JASCO can generate high-quality music samples conditioned on global text descriptions along with fine-grained local controls. JASCO is based on the Flow Matching modeling paradigm together with a novel conditioning method. This allows music generation controlled both locally (e.g., chords) and globally (text description). Specifically, we apply information bottleneck layers in conjunction with temporal blurring to extract relevant information with respect to specific controls. This allows the incorporation of both symbolic and audio-based conditions in the same text-to-music model. We experiment with various symbolic control signals (e.g., chords, melody), as well as with audio representations (e.g., separated drum tracks, full-mix). We evaluate JASCO considering both generation quality and condition adherence, using both objective metrics and human studies. Results suggest that JASCO is comparable to the evaluated baselines considering generation quality while allowing significantly better and more versatile controls over the generated music. Samples are available on our demo page https://pages.cs.huji.ac.il/adiyoss-lab/JASCO.

Masked Audio Generation using a Single Non-Autoregressive Transformer

We introduce MAGNeT, a masked generative sequence modeling method that operates directly over several streams of audio tokens. Unlike prior work, MAGNeT is comprised of a single-stage, non-autoregressive transformer. During training, we predict spans of masked tokens obtained from a masking scheduler, while during inference we gradually construct the output sequence using several decoding steps. To further enhance the quality of the generated audio, we introduce a novel rescoring method in which, we leverage an external pre-trained model to rescore and rank predictions from MAGNeT, which will be then used for later decoding steps. Lastly, we explore a hybrid version of MAGNeT, in which we fuse between autoregressive and non-autoregressive models to generate the first few seconds in an autoregressive manner while the rest of the sequence is being decoded in parallel. We demonstrate the efficiency of MAGNeT for the task of text-to-music and text-to-audio generation and conduct an extensive empirical evaluation, considering both objective metrics and human studies. The proposed approach is comparable to the evaluated baselines, while being significantly faster (x7 faster than the autoregressive baseline). Through ablation studies and analysis, we shed light on the importance of each of the components comprising MAGNeT, together with pointing to the trade-offs between autoregressive and non-autoregressive modeling, considering latency, throughput, and generation quality. Samples are available on our demo page https://pages.cs.huji.ac.il/adiyoss-lab/MAGNeT.

Depth Enables Long-Term Memory for Recurrent Neural Networks

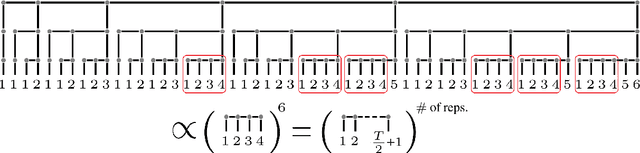
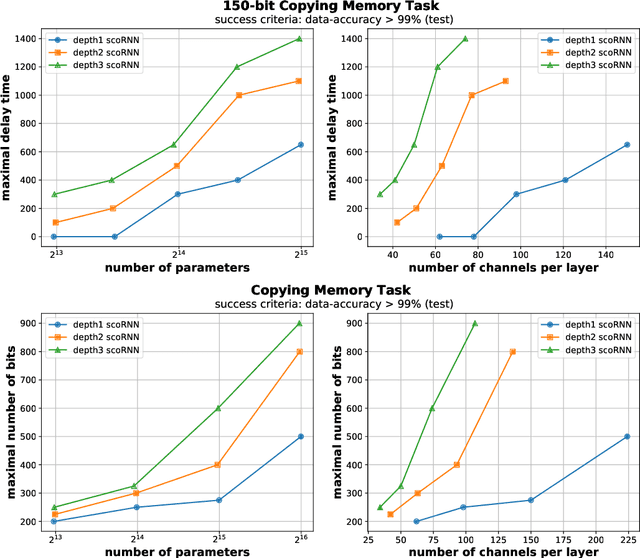
A key attribute that drives the unprecedented success of modern Recurrent Neural Networks (RNNs) on learning tasks which involve sequential data, is their ability to model intricate long-term temporal dependencies. However, a well established measure of RNNs long-term memory capacity is lacking, and thus formal understanding of the effect of depth on their ability to correlate data throughout time is limited. Specifically, existing depth efficiency results on convolutional networks do not suffice in order to account for the success of deep RNNs on data of varying lengths. In order to address this, we introduce a measure of the network's ability to support information flow across time, referred to as the Start-End separation rank, which reflects the distance of the function realized by the recurrent network from modeling no dependency between the beginning and end of the input sequence. We prove that deep recurrent networks support Start-End separation ranks which are combinatorially higher than those supported by their shallow counterparts. Thus, we establish that depth brings forth an overwhelming advantage in the ability of recurrent networks to model long-term dependencies, and provide an exemplar of quantifying this key attribute. We empirically demonstrate the discussed phenomena on common RNNs through extensive experimental evaluation using the optimization technique of restricting the hidden-to-hidden matrix to being orthogonal. Finally, we employ the tool of quantum Tensor Networks to gain additional graphic insights regarding the complexity brought forth by depth in recurrent networks.

On the Long-Term Memory of Deep Recurrent Networks

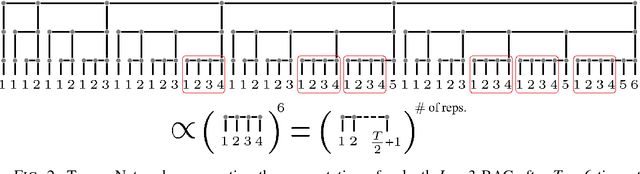
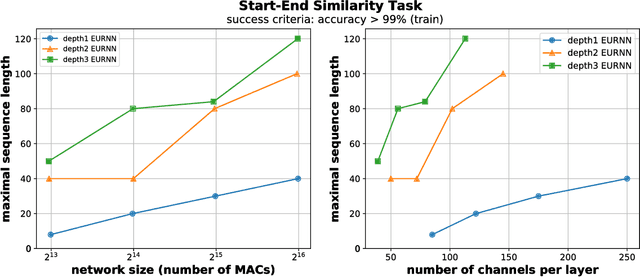
A key attribute that drives the unprecedented success of modern Recurrent Neural Networks (RNNs) on learning tasks which involve sequential data, is their ability to model intricate long-term temporal dependencies. However, a well established measure of RNNs long-term memory capacity is lacking, and thus formal understanding of the effect of depth on their ability to correlate data throughout time is limited. Specifically, existing depth efficiency results on convolutional networks do not suffice in order to account for the success of deep RNNs on data of varying lengths. In order to address this, we introduce a measure of the network's ability to support information flow across time, referred to as the Start-End separation rank, which reflects the distance of the function realized by the recurrent network from modeling no dependency between the beginning and end of the input sequence. We prove that deep recurrent networks support Start-End separation ranks which are combinatorially higher than those supported by their shallow counterparts. Thus, we establish that depth brings forth an overwhelming advantage in the ability of recurrent networks to model long-term dependencies, and provide an exemplar of quantifying this key attribute which may be readily extended to other RNN architectures of interest, e.g. variants of LSTM networks. We obtain our results by considering a class of recurrent networks referred to as Recurrent Arithmetic Circuits, which merge the hidden state with the input via the Multiplicative Integration operation, and empirically demonstrate the discussed phenomena on common RNNs. Finally, we employ the tool of quantum Tensor Networks to gain additional graphic insight regarding the complexity brought forth by depth in recurrent networks.