Learning to compile smartly for program size reduction

Compiler optimization passes are an important tool for improving program efficiency and reducing program size, but manually selecting optimization passes can be time-consuming and error-prone. While human experts have identified a few fixed sequences of optimization passes (e.g., the Clang -Oz passes) that perform well for a wide variety of programs, these sequences are not conditioned on specific programs. In this paper, we propose a novel approach that learns a policy to select passes for program size reduction, allowing for customization and adaptation to specific programs. Our approach uses a search mechanism that helps identify useful pass sequences and a GNN with customized attention that selects the optimal sequence to use. Crucially it is able to generalize to new, unseen programs, making it more flexible and general than previous approaches. We evaluate our approach on a range of programs and show that it leads to size reduction compared to traditional optimization techniques. Our results demonstrate the potential of a single policy that is able to optimize many programs.

Sobolev Norm Learning Rates for Conditional Mean Embeddings

We develop novel learning rates for conditional mean embeddings by applying the theory of interpolation for reproducing kernel Hilbert spaces (RKHS). We derive explicit, adaptive convergence rates for the sample estimator under the misspecifed setting, where the target operator is not Hilbert-Schmidt or bounded with respect to the input/output RKHSs. We demonstrate that in certain parameter regimes, we can achieve uniform convergence rates in the output RKHS. We hope our analyses will allow the much broader application of conditional mean embeddings to more complex ML/RL settings involving infinite dimensional RKHSs and continuous state spaces.

Sample Efficient Graph-Based Optimization with Noisy Observations

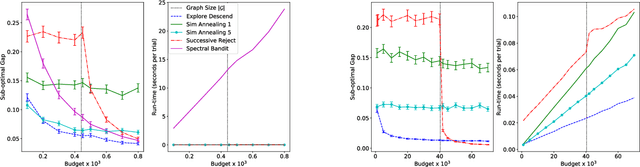
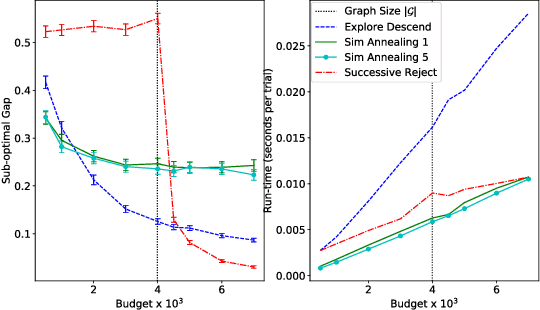
We study sample complexity of optimizing "hill-climbing friendly" functions defined on a graph under noisy observations. We define a notion of convexity, and we show that a variant of best-arm identification can find a near-optimal solution after a small number of queries that is independent of the size of the graph. For functions that have local minima and are nearly convex, we show a sample complexity for the classical simulated annealing under noisy observations. We show effectiveness of the greedy algorithm with restarts and the simulated annealing on problems of graph-based nearest neighbor classification as well as a web document re-ranking application.

A Continuation Method for Discrete Optimization and its Application to Nearest Neighbor Classification

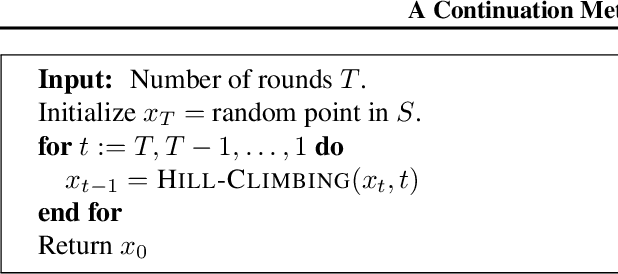
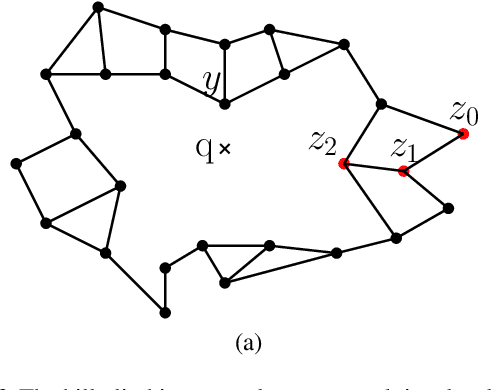
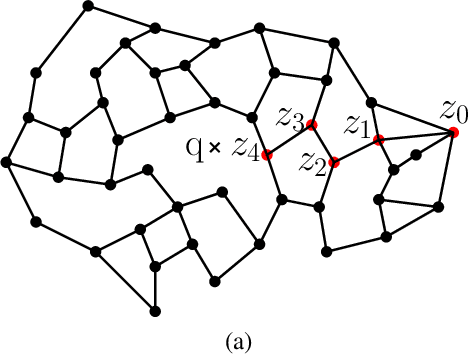
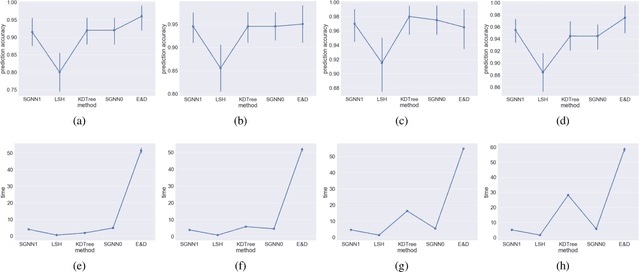
The continuation method is a popular approach in non-convex optimization and computer vision. The main idea is to start from a simple function that can be minimized efficiently, and gradually transform it to the more complicated original objective function. The solution of the simpler problem is used as the starting point to solve the original problem. We show a continuation method for discrete optimization problems. Ideally, we would like the evolved function to be hill-climbing friendly and to have the same global minima as the original function. We show that the proposed continuation method is the best affine approximation of a transformation that is guaranteed to transform the function to a hill-climbing friendly function and to have the same global minima. We show the effectiveness of the proposed technique in the problem of nearest neighbor classification. Although nearest neighbor methods are often competitive in terms of sample efficiency, the computational complexity in the test phase has been a major obstacle in their applicability in big data problems. Using the proposed continuation method, we show an improved graph-based nearest neighbor algorithm. The method is readily understood and easy to implement. We show how the computational complexity of the method in the test phase scales gracefully with the size of the training set, a property that is particularly important in big data applications.