Sample Efficient Graph-Based Optimization with Noisy Observations
Paper and Code
Jun 04, 2020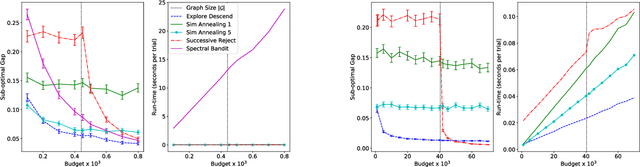
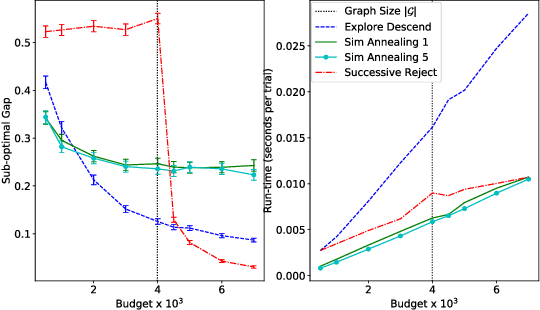
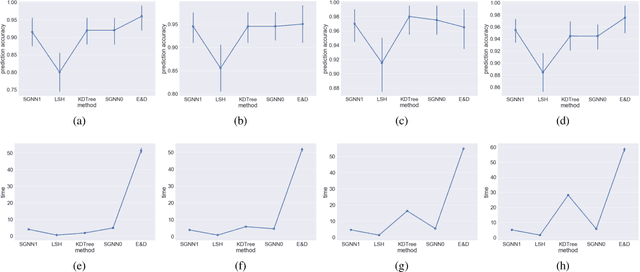
We study sample complexity of optimizing "hill-climbing friendly" functions defined on a graph under noisy observations. We define a notion of convexity, and we show that a variant of best-arm identification can find a near-optimal solution after a small number of queries that is independent of the size of the graph. For functions that have local minima and are nearly convex, we show a sample complexity for the classical simulated annealing under noisy observations. We show effectiveness of the greedy algorithm with restarts and the simulated annealing on problems of graph-based nearest neighbor classification as well as a web document re-ranking application.
* AISTATS 2019 * The first version of this paper appeared in AISTATS 2019. Thank to
community feedback, some typos and a minor issue have been identified.
Specifically, on page 4, column 2, line 18, the statement $\Delta_{1,s} \ge
(1+m)^{S-1-s} \Delta_1$ is not valid, and in the proof of Theorem 2, "By
Lemma 1" should be "By Definition 2". These problems are fixed in this
updated version published here on arxiv
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge