Few-Max: Few-Shot Domain Adaptation for Unsupervised Contrastive Representation Learning

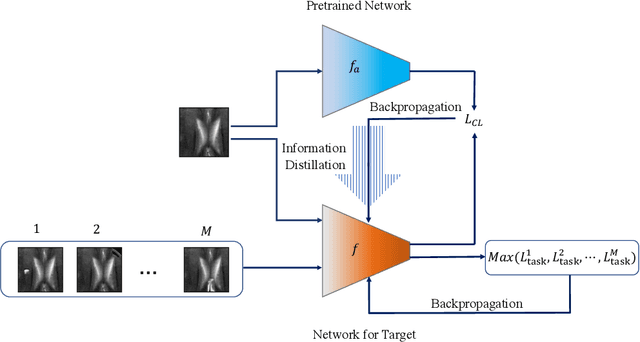
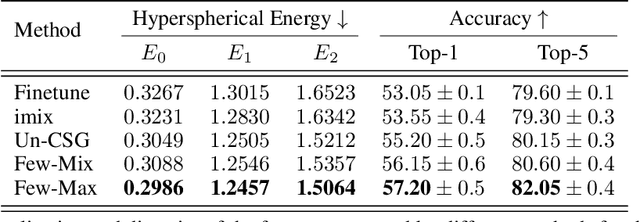
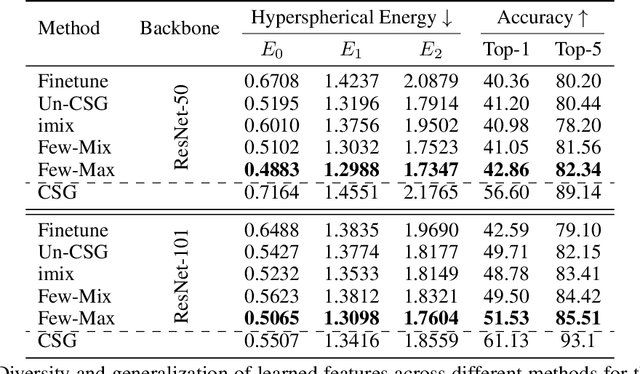
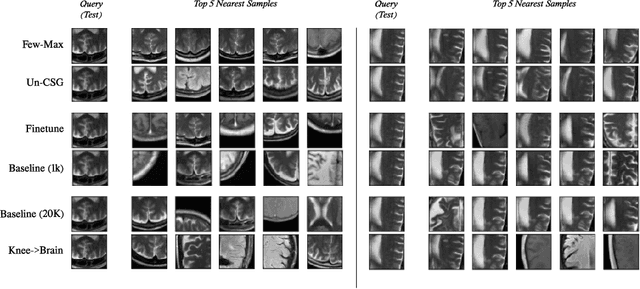
Contrastive self-supervised learning methods learn to map data points such as images into non-parametric representation space without requiring labels. While highly successful, current methods require a large amount of data in the training phase. In situations where the target training set is limited in size, generalization is known to be poor. Pretraining on a large source data set and fine-tuning on the target samples is prone to overfitting in the few-shot regime, where only a small number of target samples are available. Motivated by this, we propose a domain adaption method for self-supervised contrastive learning, termed Few-Max, to address the issue of adaptation to a target distribution under few-shot learning. To quantify the representation quality, we evaluate Few-Max on a range of source and target datasets, including ImageNet, VisDA, and fastMRI, on which Few-Max consistently outperforms other approaches.

Hyperbolic Graph Embedding with Enhanced Semi-Implicit Variational Inference

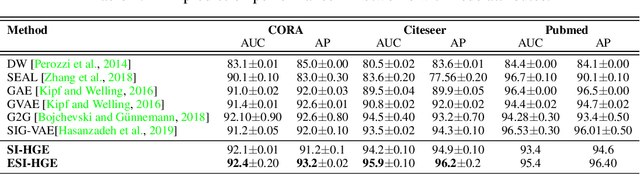
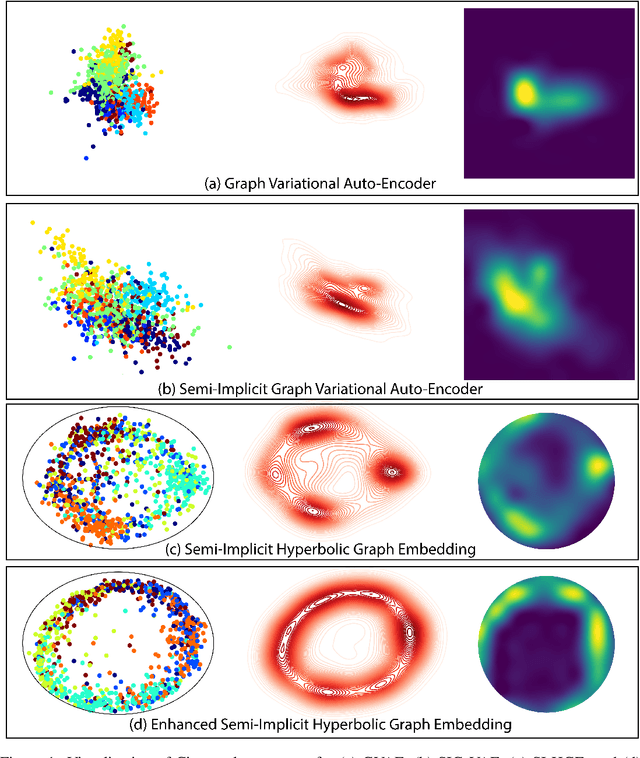
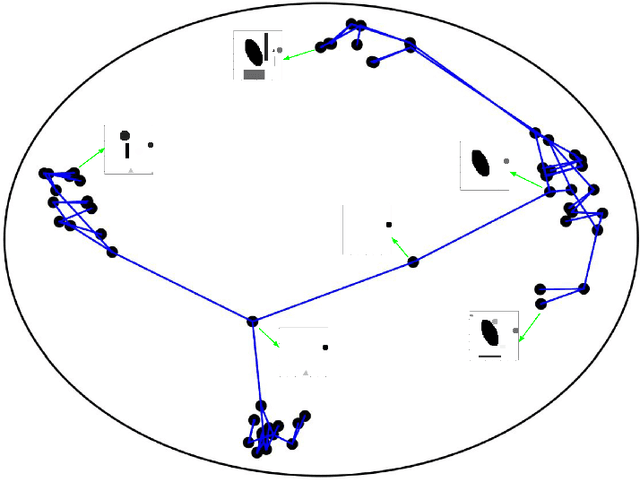
Efficient modeling of relational data arising in physical, social, and information sciences is challenging due to complicated dependencies within the data. In this work we build off of semi-implicit graph variational auto-encoders to capture higher order statistics in a low-dimensional graph latent representation. We incorporate hyperbolic geometry in the latent space through a \poincare embedding to efficiently represent graphs exhibiting hierarchical structure. To address the naive posterior latent distribution assumptions in classical variational inference, we use semi-implicit hierarchical variational Bayes to implicitly capture posteriors of given graph data, which may exhibit heavy tails, multiple modes, skewness, and highly correlated latent structures. We show that the existing semi-implicit variational inference objective provably reduces information in the observed graph. Based on this observation, we estimate and add an additional mutual information term to the semi-implicit variational inference learning objective to capture rich correlations arising between the input and latent spaces. We show that the inclusion of this regularization term in conjunction with the \poincare embedding boosts the quality of learned high-level representations and enables more flexible and faithful graphical modeling. We experimentally demonstrate that our approach outperforms existing graph variational auto-encoders both in Euclidean and in hyperbolic spaces for edge link prediction and node classification.

Long Short-Term Memory Spiking Networks and Their Applications

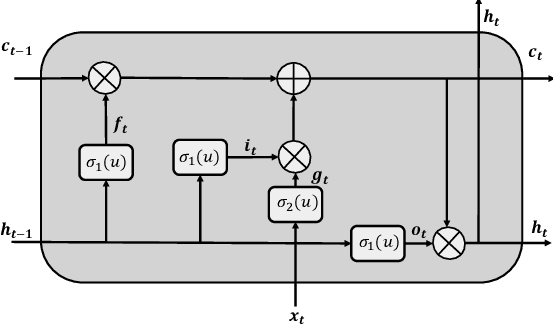
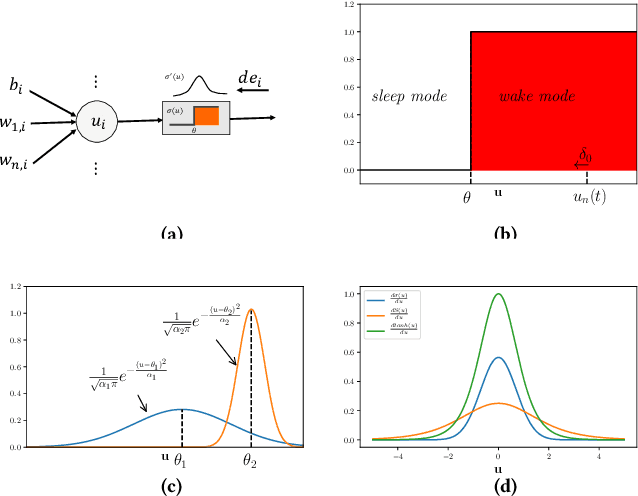
Recent advances in event-based neuromorphic systems have resulted in significant interest in the use and development of spiking neural networks (SNNs). However, the non-differentiable nature of spiking neurons makes SNNs incompatible with conventional backpropagation techniques. In spite of the significant progress made in training conventional deep neural networks (DNNs), training methods for SNNs still remain relatively poorly understood. In this paper, we present a novel framework for training recurrent SNNs. Analogous to the benefits presented by recurrent neural networks (RNNs) in learning time series models within DNNs, we develop SNNs based on long short-term memory (LSTM) networks. We show that LSTM spiking networks learn the timing of the spikes and temporal dependencies. We also develop a methodology for error backpropagation within LSTM-based SNNs. The developed architecture and method for backpropagation within LSTM-based SNNs enable them to learn long-term dependencies with comparable results to conventional LSTMs.

Learning Representations by Maximizing Mutual Information in Variational Autoencoders

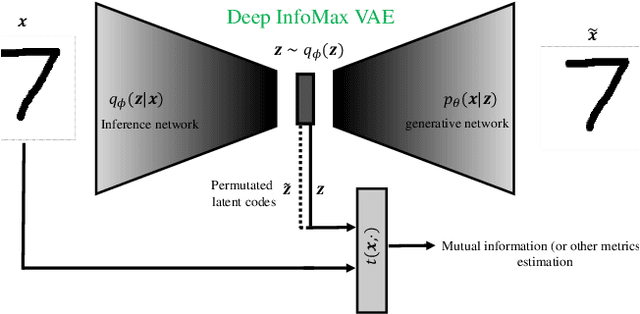
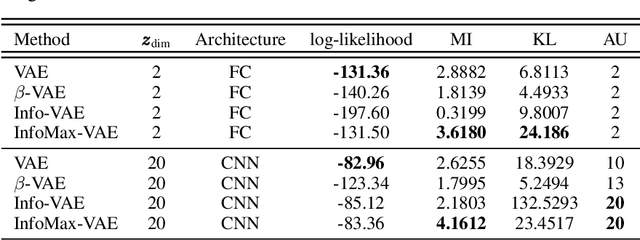
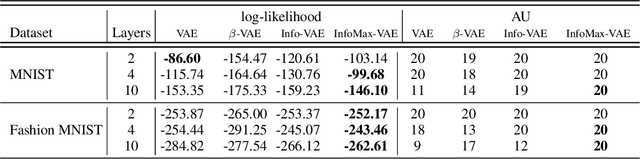
Variational autoencoders (VAEs) have ushered in a new era of unsupervised learning methods for complex distributions. Although these techniques are elegant in their approach, they are typically not useful for representation learning. In this work, we propose a simple yet powerful class of VAEs that simultaneously result in meaningful learned representations. Our solution is to combine traditional VAEs with mutual information maximization, with the goal to enhance amortized inference in VAEs using Information Theoretic techniques. We call this approach InfoMax-VAE, and such an approach can significantly boost the quality of learned high-level representations. We realize this through the explicit maximization of information measures associated with the representation. Using extensive experiments on varied datasets and setups, we show that InfoMax-VAE outperforms contemporary popular approaches, including Info-VAE and $\beta$-VAE.

Learning Representations by Maximizing Mutual Information in Variational Autoencoder

Variational autoencoders (VAE) have ushered in a new era of unsupervised learning methods for complex distributions. Although these techniques are elegant in their approach, they are typically not useful for representation learning. In this work, we propose a simple yet powerful class of VAEs that simultaneously result in meaningful learned representations. Our solution is to combine traditional VAEs with mutual information maximization, with the goal to enhance amortized inference in VAEs using Information Theoretic techniques. We call this approach InfoMax-VAE, and such an approach can significantly boost the quality of learned high-level representations. We realize this through the explicit maximization of information measures associated with the representation. Using extensive experiments on varied datasets and setups, we show that InfoMax-VAE outperforms contemporary popular approaches, including Info-VAE and $\beta$-VAE.