Learning Representations by Maximizing Mutual Information in Variational Autoencoders
Paper and Code
Jan 07, 2020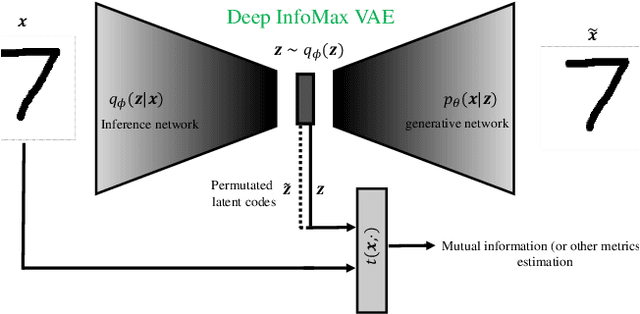
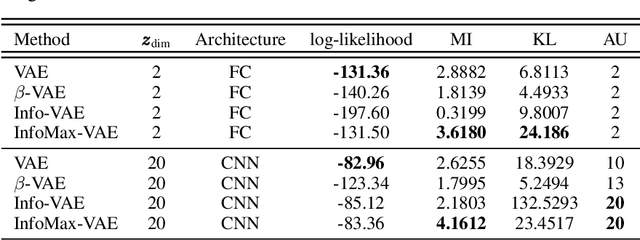

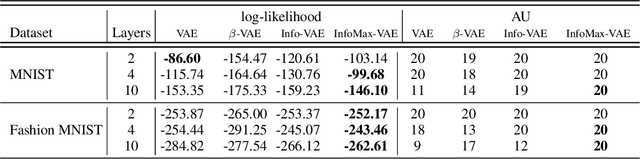
Variational autoencoders (VAEs) have ushered in a new era of unsupervised learning methods for complex distributions. Although these techniques are elegant in their approach, they are typically not useful for representation learning. In this work, we propose a simple yet powerful class of VAEs that simultaneously result in meaningful learned representations. Our solution is to combine traditional VAEs with mutual information maximization, with the goal to enhance amortized inference in VAEs using Information Theoretic techniques. We call this approach InfoMax-VAE, and such an approach can significantly boost the quality of learned high-level representations. We realize this through the explicit maximization of information measures associated with the representation. Using extensive experiments on varied datasets and setups, we show that InfoMax-VAE outperforms contemporary popular approaches, including Info-VAE and $\beta$-VAE.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge