Rahi Kalantari
Hyperbolic Graph Embedding with Enhanced Semi-Implicit Variational Inference
Oct 31, 2020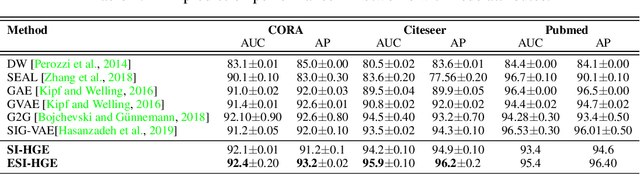
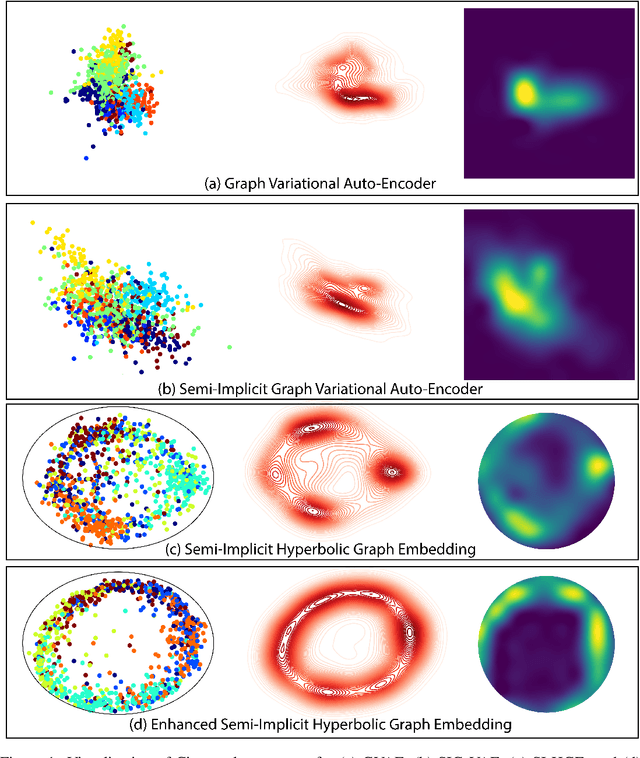

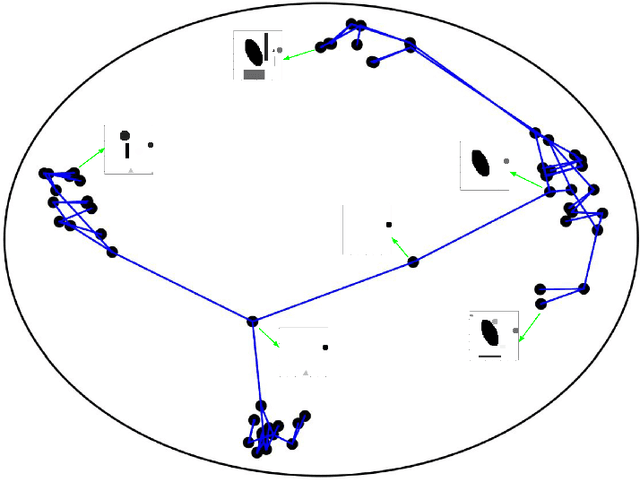
Abstract:Efficient modeling of relational data arising in physical, social, and information sciences is challenging due to complicated dependencies within the data. In this work we build off of semi-implicit graph variational auto-encoders to capture higher order statistics in a low-dimensional graph latent representation. We incorporate hyperbolic geometry in the latent space through a \poincare embedding to efficiently represent graphs exhibiting hierarchical structure. To address the naive posterior latent distribution assumptions in classical variational inference, we use semi-implicit hierarchical variational Bayes to implicitly capture posteriors of given graph data, which may exhibit heavy tails, multiple modes, skewness, and highly correlated latent structures. We show that the existing semi-implicit variational inference objective provably reduces information in the observed graph. Based on this observation, we estimate and add an additional mutual information term to the semi-implicit variational inference learning objective to capture rich correlations arising between the input and latent spaces. We show that the inclusion of this regularization term in conjunction with the \poincare embedding boosts the quality of learned high-level representations and enables more flexible and faithful graphical modeling. We experimentally demonstrate that our approach outperforms existing graph variational auto-encoders both in Euclidean and in hyperbolic spaces for edge link prediction and node classification.
Graph Gamma Process Generalized Linear Dynamical Systems
Jul 25, 2020
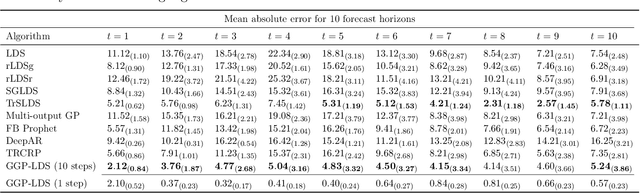


Abstract:We introduce graph gamma process (GGP) linear dynamical systems to model real-valued multivariate time series. For temporal pattern discovery, the latent representation under the model is used to decompose the time series into a parsimonious set of multivariate sub-sequences. In each sub-sequence, different data dimensions often share similar temporal patterns but may exhibit distinct magnitudes, and hence allowing the superposition of all sub-sequences to exhibit diverse behaviors at different data dimensions. We further generalize the proposed model by replacing the Gaussian observation layer with the negative binomial distribution to model multivariate count time series. Generated from the proposed GGP is an infinite dimensional directed sparse random graph, which is constructed by taking the logical OR operation of countably infinite binary adjacency matrices that share the same set of countably infinite nodes. Each of these adjacency matrices is associated with a weight to indicate its activation strength, and places a finite number of edges between a finite subset of nodes belonging to the same node community. We use the generated random graph, whose number of nonzero-degree nodes is finite, to define both the sparsity pattern and dimension of the latent state transition matrix of a (generalized) linear dynamical system. The activation strength of each node community relative to the overall activation strength is used to extract a multivariate sub-sequence, revealing the data pattern captured by the corresponding community. On both synthetic and real-world time series, the proposed nonparametric Bayesian dynamic models, which are initialized at random, consistently exhibit good predictive performance in comparison to a variety of baseline models, revealing interpretable latent state transition patterns and decomposing the time series into distinctly behaved sub-sequences.
Nonparametric Bayesian Sparse Graph Linear Dynamical Systems
Feb 21, 2018
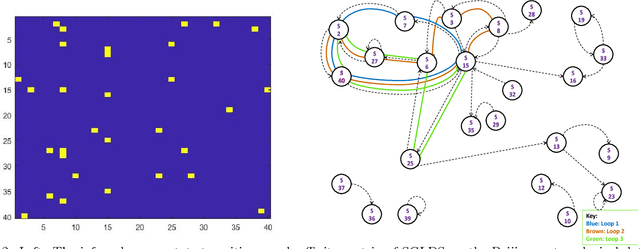

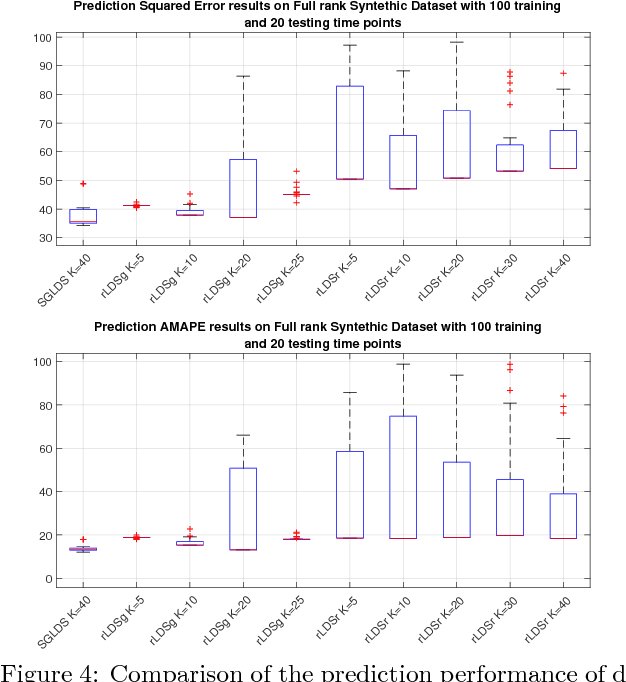
Abstract:A nonparametric Bayesian sparse graph linear dynamical system (SGLDS) is proposed to model sequentially observed multivariate data. SGLDS uses the Bernoulli-Poisson link together with a gamma process to generate an infinite dimensional sparse random graph to model state transitions. Depending on the sparsity pattern of the corresponding row and column of the graph affinity matrix, a latent state of SGLDS can be categorized as either a non-dynamic state or a dynamic one. A normal-gamma construction is used to shrink the energy captured by the non-dynamic states, while the dynamic states can be further categorized into live, absorbing, or noise-injection states, which capture different types of dynamical components of the underlying time series. The state-of-the-art performance of SGLDS is demonstrated with experiments on both synthetic and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge