Graph Gamma Process Generalized Linear Dynamical Systems
Paper and Code
Jul 25, 2020
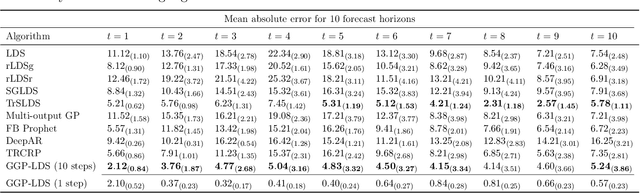


We introduce graph gamma process (GGP) linear dynamical systems to model real-valued multivariate time series. For temporal pattern discovery, the latent representation under the model is used to decompose the time series into a parsimonious set of multivariate sub-sequences. In each sub-sequence, different data dimensions often share similar temporal patterns but may exhibit distinct magnitudes, and hence allowing the superposition of all sub-sequences to exhibit diverse behaviors at different data dimensions. We further generalize the proposed model by replacing the Gaussian observation layer with the negative binomial distribution to model multivariate count time series. Generated from the proposed GGP is an infinite dimensional directed sparse random graph, which is constructed by taking the logical OR operation of countably infinite binary adjacency matrices that share the same set of countably infinite nodes. Each of these adjacency matrices is associated with a weight to indicate its activation strength, and places a finite number of edges between a finite subset of nodes belonging to the same node community. We use the generated random graph, whose number of nonzero-degree nodes is finite, to define both the sparsity pattern and dimension of the latent state transition matrix of a (generalized) linear dynamical system. The activation strength of each node community relative to the overall activation strength is used to extract a multivariate sub-sequence, revealing the data pattern captured by the corresponding community. On both synthetic and real-world time series, the proposed nonparametric Bayesian dynamic models, which are initialized at random, consistently exhibit good predictive performance in comparison to a variety of baseline models, revealing interpretable latent state transition patterns and decomposing the time series into distinctly behaved sub-sequences.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge