Aggregated Learning: A Vector-Quantization Approach to Learning Neural Network Classifiers

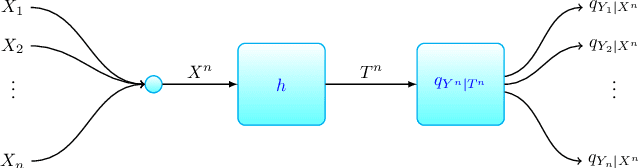
We consider the problem of learning a neural network classifier. Under the information bottleneck (IB) principle, we associate with this classification problem a representation learning problem, which we call "IB learning". We show that IB learning is, in fact, equivalent to a special class of the quantization problem. The classical results in rate-distortion theory then suggest that IB learning can benefit from a "vector quantization" approach, namely, simultaneously learning the representations of multiple input objects. Such an approach assisted with some variational techniques, result in a novel learning framework, "Aggregated Learning", for classification with neural network models. In this framework, several objects are jointly classified by a single neural network. The effectiveness of this framework is verified through extensive experiments on standard image recognition and text classification tasks.

Neural Entropic Estimation: A faster path to mutual information estimation

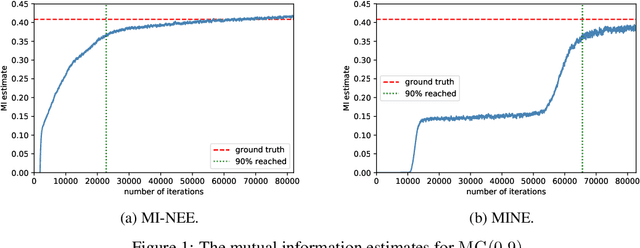
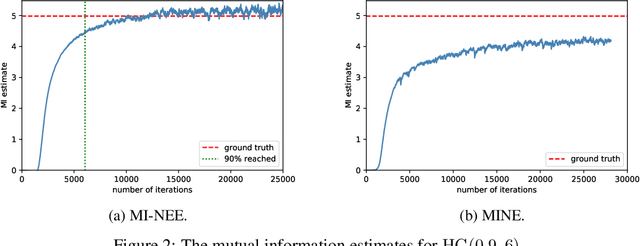
We point out a limitation of the mutual information neural estimation (MINE) where the network fails to learn at the initial training phase, leading to slow convergence in the number of training iterations. To solve this problem, we propose a faster method called the mutual information neural entropic estimation (MI-NEE). Our solution first generalizes MINE to estimate the entropy using a custom reference distribution. The entropy estimate can then be used to estimate the mutual information. We argue that the seemingly redundant intermediate step of entropy estimation allows one to improve the convergence by an appropriate reference distribution. In particular, we show that MI-NEE reduces to MINE in the special case when the reference distribution is the product of marginal distributions, but faster convergence is possible by choosing the uniform distribution as the reference distribution instead. Compared to the product of marginals, the uniform distribution introduces more samples in low-density regions and fewer samples in high-density regions, which appear to lead to an overall larger gradient for faster convergence.

Agglomerative Info-Clustering

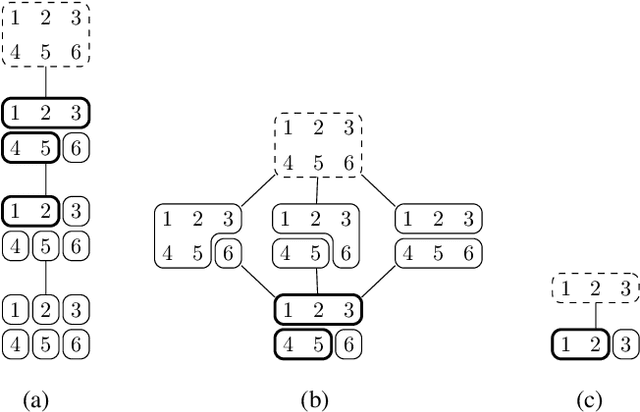
An agglomerative clustering of random variables is proposed, where clusters of random variables sharing the maximum amount of multivariate mutual information are merged successively to form larger clusters. Compared to the previous info-clustering algorithms, the agglomerative approach allows the computation to stop earlier when clusters of desired size and accuracy are obtained. An efficient algorithm is also derived based on the submodularity of entropy and the duality between the principal sequence of partitions and the principal sequence for submodular functions.

Duality between Feature Selection and Data Clustering

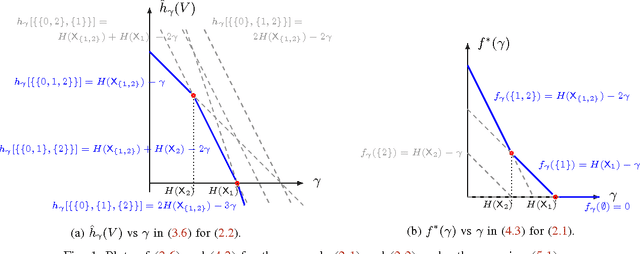
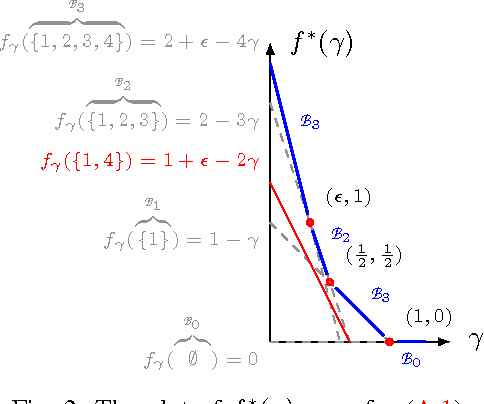
The feature-selection problem is formulated from an information-theoretic perspective. We show that the problem can be efficiently solved by an extension of the recently proposed info-clustering paradigm. This reveals the fundamental duality between feature selection and data clustering,which is a consequence of the more general duality between the principal partition and the principal lattice of partitions in combinatorial optimization.