Chung Chan
Targeted Gradient Descent: A Novel Method for Convolutional Neural Networks Fine-tuning and Online-learning
Sep 29, 2021



Abstract:A convolutional neural network (ConvNet) is usually trained and then tested using images drawn from the same distribution. To generalize a ConvNet to various tasks often requires a complete training dataset that consists of images drawn from different tasks. In most scenarios, it is nearly impossible to collect every possible representative dataset as a priori. The new data may only become available after the ConvNet is deployed in clinical practice. ConvNet, however, may generate artifacts on out-of-distribution testing samples. In this study, we present Targeted Gradient Descent (TGD), a novel fine-tuning method that can extend a pre-trained network to a new task without revisiting data from the previous task while preserving the knowledge acquired from previous training. To a further extent, the proposed method also enables online learning of patient-specific data. The method is built on the idea of reusing a pre-trained ConvNet's redundant kernels to learn new knowledge. We compare the performance of TGD to several commonly used training approaches on the task of Positron emission tomography (PET) image denoising. Results from clinical images show that TGD generated results on par with training-from-scratch while significantly reducing data preparation and network training time. More importantly, it enables online learning on the testing study to enhance the network's generalization capability in real-world applications.
Neural Entropic Estimation: A faster path to mutual information estimation
May 31, 2019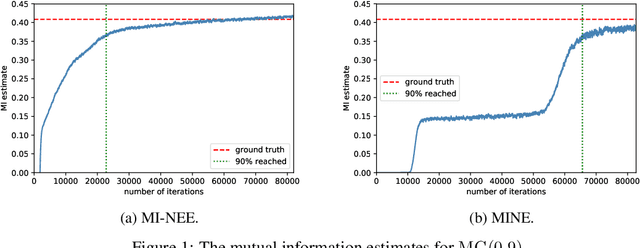
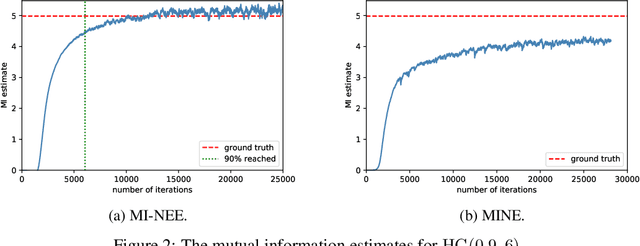
Abstract:We point out a limitation of the mutual information neural estimation (MINE) where the network fails to learn at the initial training phase, leading to slow convergence in the number of training iterations. To solve this problem, we propose a faster method called the mutual information neural entropic estimation (MI-NEE). Our solution first generalizes MINE to estimate the entropy using a custom reference distribution. The entropy estimate can then be used to estimate the mutual information. We argue that the seemingly redundant intermediate step of entropy estimation allows one to improve the convergence by an appropriate reference distribution. In particular, we show that MI-NEE reduces to MINE in the special case when the reference distribution is the product of marginal distributions, but faster convergence is possible by choosing the uniform distribution as the reference distribution instead. Compared to the product of marginals, the uniform distribution introduces more samples in low-density regions and fewer samples in high-density regions, which appear to lead to an overall larger gradient for faster convergence.
Agglomerative Info-Clustering
Feb 24, 2017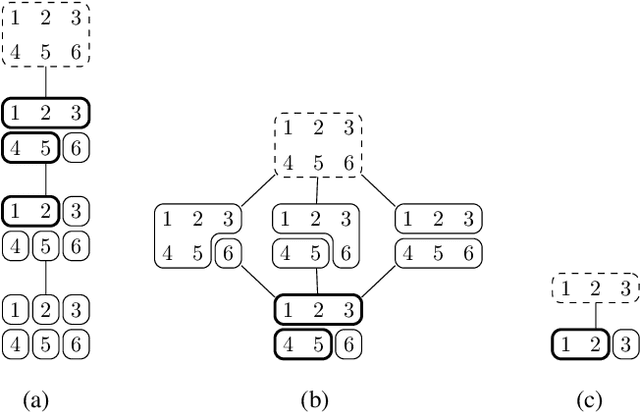
Abstract:An agglomerative clustering of random variables is proposed, where clusters of random variables sharing the maximum amount of multivariate mutual information are merged successively to form larger clusters. Compared to the previous info-clustering algorithms, the agglomerative approach allows the computation to stop earlier when clusters of desired size and accuracy are obtained. An efficient algorithm is also derived based on the submodularity of entropy and the duality between the principal sequence of partitions and the principal sequence for submodular functions.
Duality between Feature Selection and Data Clustering
Oct 05, 2016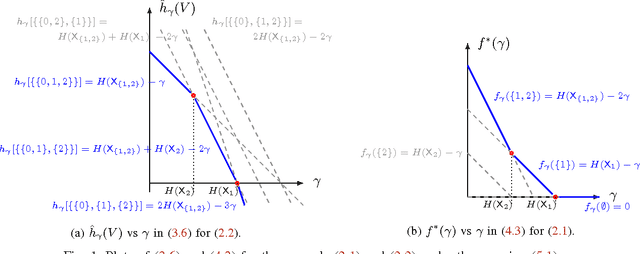
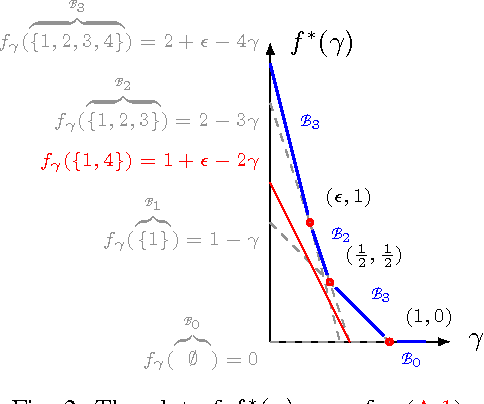
Abstract:The feature-selection problem is formulated from an information-theoretic perspective. We show that the problem can be efficiently solved by an extension of the recently proposed info-clustering paradigm. This reveals the fundamental duality between feature selection and data clustering,which is a consequence of the more general duality between the principal partition and the principal lattice of partitions in combinatorial optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge