GTEA: Representation Learning for Temporal Interaction Graphs via Edge Aggregation

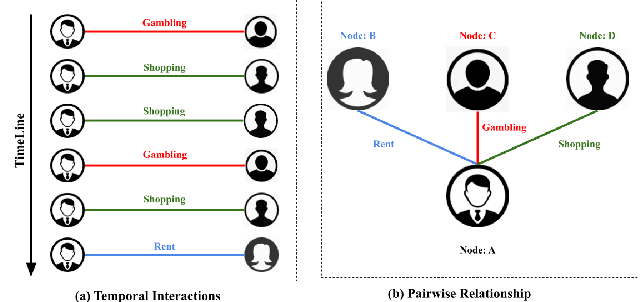
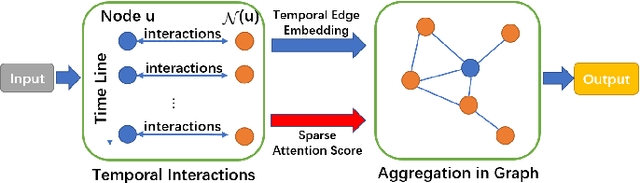
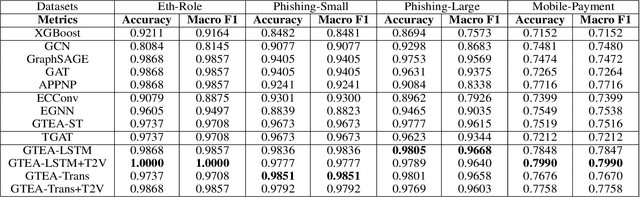
We consider the problem of representation learning for temporal interaction graphs where a network of entities with complex interactions over an extended period of time is modeled as a graph with a rich set of node and edge attributes. In particular, an edge between a node-pair within the graph corresponds to a multi-dimensional time-series. To fully capture and model the dynamics of the network, we propose GTEA, a framework of representation learning for temporal interaction graphs with per-edge time-based aggregation. Under GTEA, a Graph Neural Network (GNN) is integrated with a state-of-the-art sequence model, such as LSTM, Transformer and their time-aware variants. The sequence model generates edge embeddings to encode temporal interaction patterns between each pair of nodes, while the GNN-based backbone learns the topological dependencies and relationships among different nodes. GTEA also incorporates a sparsity-inducing self-attention mechanism to distinguish and focus on the more important neighbors of each node during the aggregation process. By capturing temporal interactive dynamics together with multi-dimensional node and edge attributes in a network, GTEA can learn fine-grained representations for a temporal interaction graph to enable or facilitate other downstream data analytic tasks. Experimental results show that GTEA outperforms state-of-the-art schemes including GraphSAGE, APPNP, and TGAT by delivering higher accuracy (100.00%, 98.51%, 98.05% ,79.90%) and macro-F1 score (100.00%, 98.51%, 96.68% ,79.90%) over four large-scale real-world datasets for binary/ multi-class node classification.

Identifying Illicit Accounts in Large Scale E-payment Networks -- A Graph Representation Learning Approach

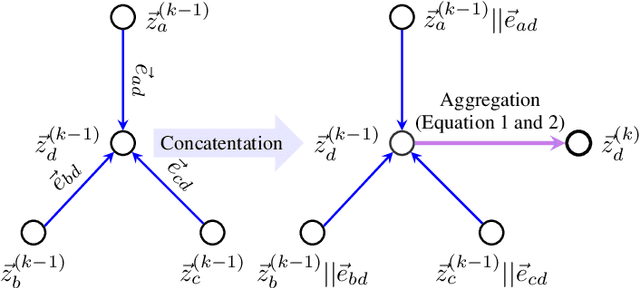
Rapid and massive adoption of mobile/ online payment services has brought new challenges to the service providers as well as regulators in safeguarding the proper uses such services/ systems. In this paper, we leverage recent advances in deep-neural-network-based graph representation learning to detect abnormal/ suspicious financial transactions in real-world e-payment networks. In particular, we propose an end-to-end Graph Convolution Network (GCN)-based algorithm to learn the embeddings of the nodes and edges of a large-scale time-evolving graph. In the context of e-payment transaction graphs, the resultant node and edge embeddings can effectively characterize the user-background as well as the financial transaction patterns of individual account holders. As such, we can use the graph embedding results to drive downstream graph mining tasks such as node-classification to identify illicit accounts within the payment networks. Our algorithm outperforms state-of-the-art schemes including GraphSAGE, Gradient Boosting Decision Tree and Random Forest to deliver considerably higher accuracy (94.62% and 86.98% respectively) in classifying user accounts within 2 practical e-payment transaction datasets. It also achieves outstanding accuracy (97.43%) for another biomedical entity identification task while using only edge-related information.

Neural Entropic Estimation: A faster path to mutual information estimation

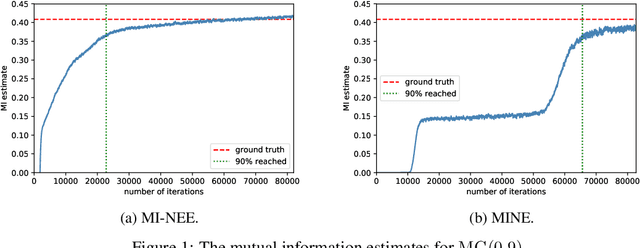
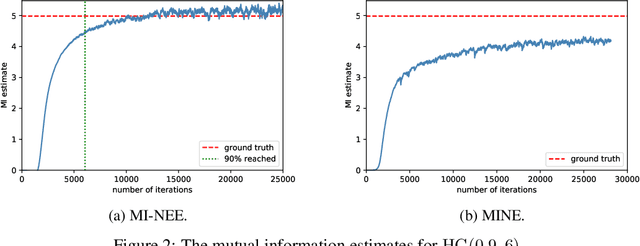
We point out a limitation of the mutual information neural estimation (MINE) where the network fails to learn at the initial training phase, leading to slow convergence in the number of training iterations. To solve this problem, we propose a faster method called the mutual information neural entropic estimation (MI-NEE). Our solution first generalizes MINE to estimate the entropy using a custom reference distribution. The entropy estimate can then be used to estimate the mutual information. We argue that the seemingly redundant intermediate step of entropy estimation allows one to improve the convergence by an appropriate reference distribution. In particular, we show that MI-NEE reduces to MINE in the special case when the reference distribution is the product of marginal distributions, but faster convergence is possible by choosing the uniform distribution as the reference distribution instead. Compared to the product of marginals, the uniform distribution introduces more samples in low-density regions and fewer samples in high-density regions, which appear to lead to an overall larger gradient for faster convergence.