Qiaoqiao Zhou
Agglomerative Info-Clustering
Feb 24, 2017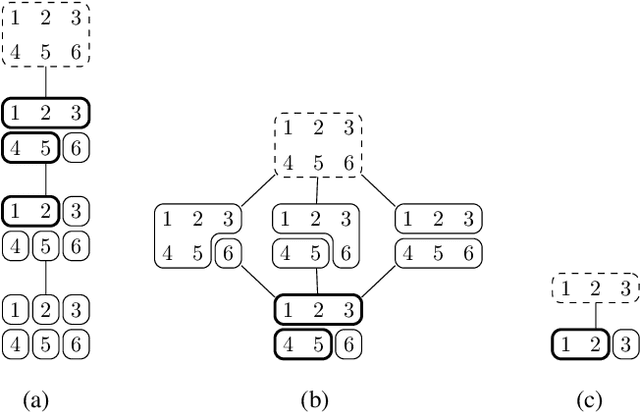
Abstract:An agglomerative clustering of random variables is proposed, where clusters of random variables sharing the maximum amount of multivariate mutual information are merged successively to form larger clusters. Compared to the previous info-clustering algorithms, the agglomerative approach allows the computation to stop earlier when clusters of desired size and accuracy are obtained. An efficient algorithm is also derived based on the submodularity of entropy and the duality between the principal sequence of partitions and the principal sequence for submodular functions.
Duality between Feature Selection and Data Clustering
Oct 05, 2016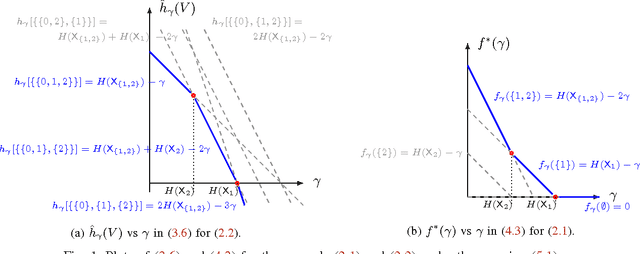
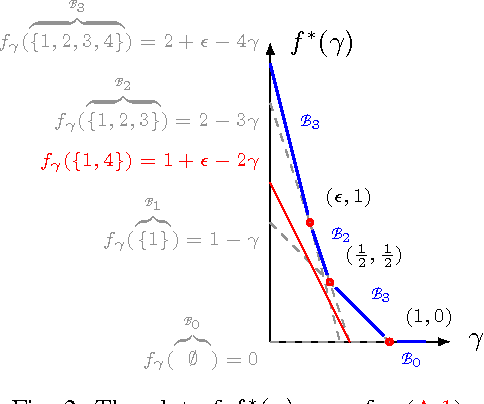
Abstract:The feature-selection problem is formulated from an information-theoretic perspective. We show that the problem can be efficiently solved by an extension of the recently proposed info-clustering paradigm. This reveals the fundamental duality between feature selection and data clustering,which is a consequence of the more general duality between the principal partition and the principal lattice of partitions in combinatorial optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge