Neighborhood Adaptive Estimators for Causal Inference under Network Interference

Estimating causal effects has become an integral part of most applied fields. Solving these modern causal questions requires tackling violations of many classical causal assumptions. In this work we consider the violation of the classical no-interference assumption, meaning that the treatment of one individuals might affect the outcomes of another. To make interference tractable, we consider a known network that describes how interference may travel. However, unlike previous work in this area, the radius (and intensity) of the interference experienced by a unit is unknown and can depend on different sub-networks of those treated and untreated that are connected to this unit. We study estimators for the average direct treatment effect on the treated in such a setting. The proposed estimator builds upon a Lepski-like procedure that searches over the possible relevant radii and treatment assignment patterns. In contrast to previous work, the proposed procedure aims to approximate the relevant network interference patterns. We establish oracle inequalities and corresponding adaptive rates for the estimation of the interference function. We leverage such estimates to propose and analyze two estimators for the average direct treatment effect on the treated. We address several challenges steaming from the data-driven creation of the patterns (i.e. feature engineering) and the network dependence. In addition to rates of convergence, under mild regularity conditions, we show that one of the proposed estimators is asymptotically normal and unbiased.

Latent Agents in Networks: Estimation and Pricing

We focus on a setting where agents in a social network consume a product that exhibits positive local network externalities. A seller has access to data on past consumption decisions/prices for a subset of observable agents, and can target these agents with appropriate discounts to exploit network effects and increase her revenues. A novel feature of the model is that the observable agents potentially interact with additional latent agents. These latent agents can purchase the same product from a different channel, and are not observed by the seller. Observable agents influence each other both directly and indirectly through the influence they exert on the latent part. The seller knows the connection structure of neither the observable nor the latent part of the network. We investigate how the seller can use the available data to estimate the matrix that captures the dependence of observable agents' consumption decisions on the prices offered to them. We provide an algorithm for estimating this matrix under an approximate sparsity condition, and obtain convergence rates for the proposed estimator despite the high-dimensionality that allows more agents than observations. Importantly, we then show that this approximate sparsity condition holds under standard conditions present in the literature and hence our algorithms are applicable to a large class of networks. We establish that by using the estimated matrix the seller can construct prices that lead to a small revenue loss relative to revenue-maximizing prices under complete information, and the optimality gap vanishes relative to the size of the network. We also illustrate that the presence of latent agents leads to significant changes in the structure of the revenue-maximizing prices.

Program Evaluation and Causal Inference with High-Dimensional Data

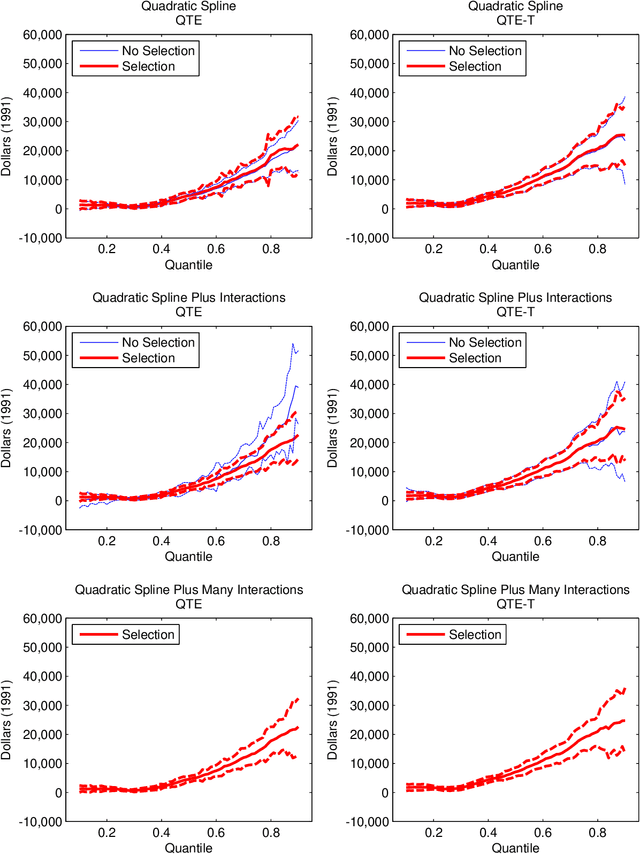
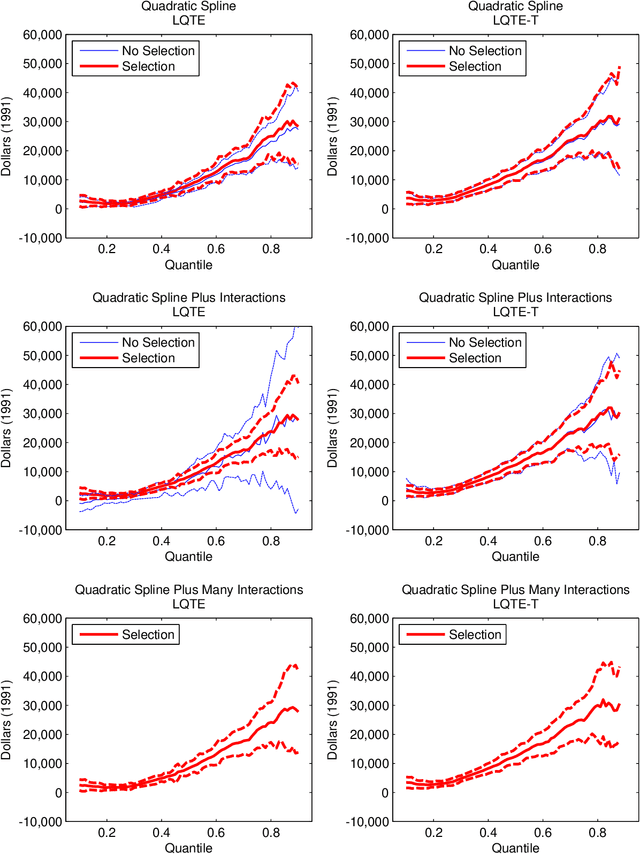
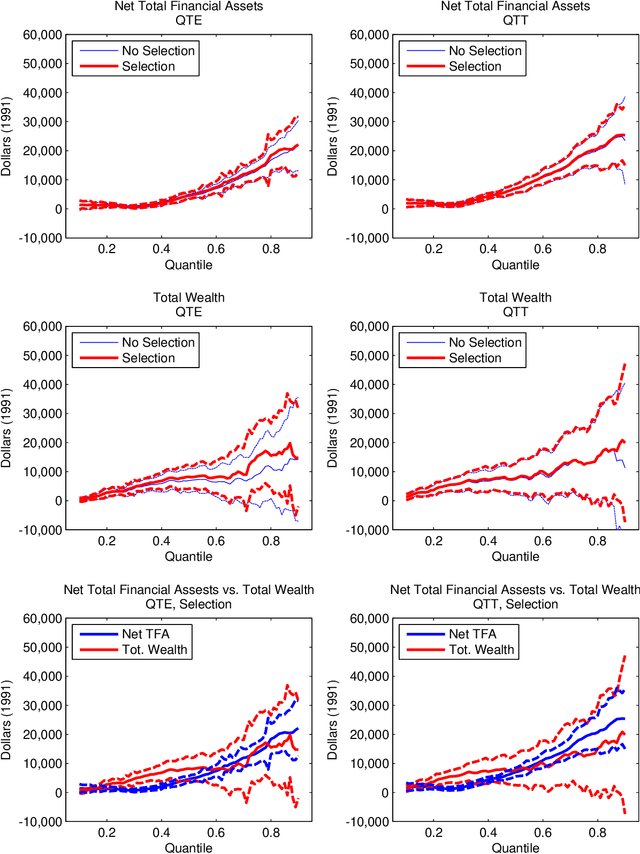
In this paper, we provide efficient estimators and honest confidence bands for a variety of treatment effects including local average (LATE) and local quantile treatment effects (LQTE) in data-rich environments. We can handle very many control variables, endogenous receipt of treatment, heterogeneous treatment effects, and function-valued outcomes. Our framework covers the special case of exogenous receipt of treatment, either conditional on controls or unconditionally as in randomized control trials. In the latter case, our approach produces efficient estimators and honest bands for (functional) average treatment effects (ATE) and quantile treatment effects (QTE). To make informative inference possible, we assume that key reduced form predictive relationships are approximately sparse. This assumption allows the use of regularization and selection methods to estimate those relations, and we provide methods for post-regularization and post-selection inference that are uniformly valid (honest) across a wide-range of models. We show that a key ingredient enabling honest inference is the use of orthogonal or doubly robust moment conditions in estimating certain reduced form functional parameters. We illustrate the use of the proposed methods with an application to estimating the effect of 401(k) eligibility and participation on accumulated assets.

Escaping the Local Minima via Simulated Annealing: Optimization of Approximately Convex Functions

We consider the problem of optimizing an approximately convex function over a bounded convex set in $\mathbb{R}^n$ using only function evaluations. The problem is reduced to sampling from an \emph{approximately} log-concave distribution using the Hit-and-Run method, which is shown to have the same $\mathcal{O}^*$ complexity as sampling from log-concave distributions. In addition to extend the analysis for log-concave distributions to approximate log-concave distributions, the implementation of the 1-dimensional sampler of the Hit-and-Run walk requires new methods and analysis. The algorithm then is based on simulated annealing which does not relies on first order conditions which makes it essentially immune to local minima. We then apply the method to different motivating problems. In the context of zeroth order stochastic convex optimization, the proposed method produces an $\epsilon$-minimizer after $\mathcal{O}^*(n^{7.5}\epsilon^{-2})$ noisy function evaluations by inducing a $\mathcal{O}(\epsilon/n)$-approximately log concave distribution. We also consider in detail the case when the "amount of non-convexity" decays towards the optimum of the function. Other applications of the method discussed in this work include private computation of empirical risk minimizers, two-stage stochastic programming, and approximate dynamic programming for online learning.

An $\{l_1,l_2,l_{\infty}\}$-Regularization Approach to High-Dimensional Errors-in-variables Models

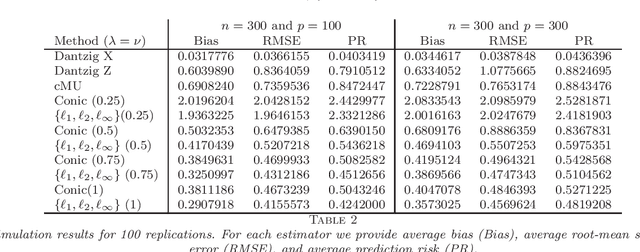
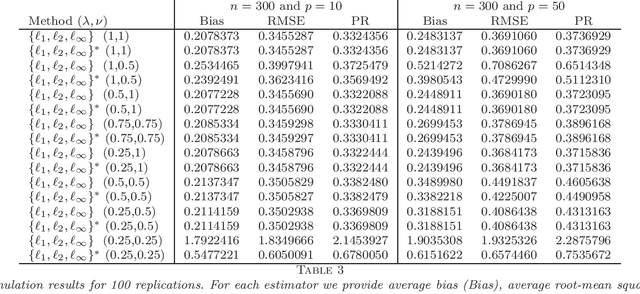
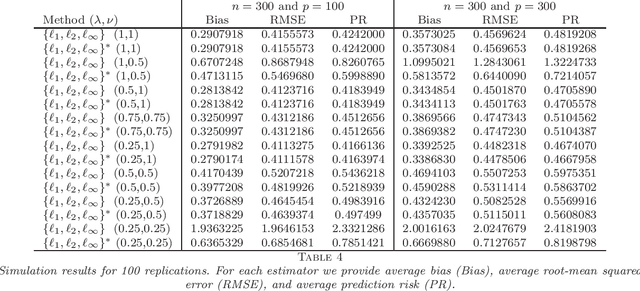
Several new estimation methods have been recently proposed for the linear regression model with observation error in the design. Different assumptions on the data generating process have motivated different estimators and analysis. In particular, the literature considered (1) observation errors in the design uniformly bounded by some $\bar \delta$, and (2) zero mean independent observation errors. Under the first assumption, the rates of convergence of the proposed estimators depend explicitly on $\bar \delta$, while the second assumption has been applied when an estimator for the second moment of the observational error is available. This work proposes and studies two new estimators which, compared to other procedures for regression models with errors in the design, exploit an additional $l_{\infty}$-norm regularization. The first estimator is applicable when both (1) and (2) hold but does not require an estimator for the second moment of the observational error. The second estimator is applicable under (2) and requires an estimator for the second moment of the observation error. Importantly, we impose no assumption on the accuracy of this pilot estimator, in contrast to the previously known procedures. As the recent proposals, we allow the number of covariates to be much larger than the sample size. We establish the rates of convergence of the estimators and compare them with the bounds obtained for related estimators in the literature. These comparisons show interesting insights on the interplay of the assumptions and the achievable rates of convergence.