Drift Control of High-Dimensional RBM: A Computational Method Based on Neural Networks

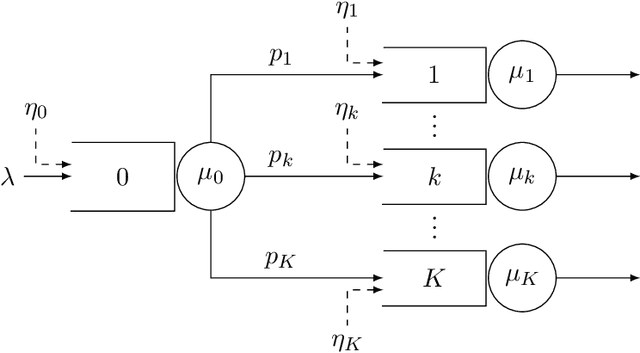
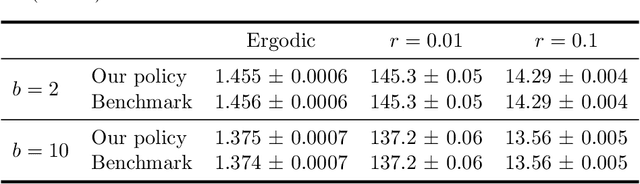
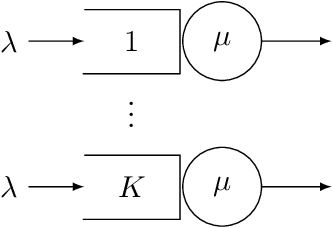
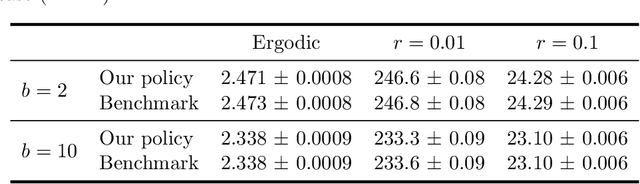
Motivated by applications in queueing theory, we consider a stochastic control problem whose state space is the $d$-dimensional positive orthant. The controlled process $Z$ evolves as a reflected Brownian motion whose covariance matrix is exogenously specified, as are its directions of reflection from the orthant's boundary surfaces. A system manager chooses a drift vector $\theta(t)$ at each time $t$ based on the history of $Z$, and the cost rate at time $t$ depends on both $Z(t)$ and $\theta(t)$. In our initial problem formulation, the objective is to minimize expected discounted cost over an infinite planning horizon, after which we treat the corresponding ergodic control problem. Extending earlier work by Han et al. (Proceedings of the National Academy of Sciences, 2018, 8505-8510), we develop and illustrate a simulation-based computational method that relies heavily on deep neural network technology. For test problems studied thus far, our method is accurate to within a fraction of one percent, and is computationally feasible in dimensions up to at least $d=30$.

Latent Agents in Networks: Estimation and Pricing

We focus on a setting where agents in a social network consume a product that exhibits positive local network externalities. A seller has access to data on past consumption decisions/prices for a subset of observable agents, and can target these agents with appropriate discounts to exploit network effects and increase her revenues. A novel feature of the model is that the observable agents potentially interact with additional latent agents. These latent agents can purchase the same product from a different channel, and are not observed by the seller. Observable agents influence each other both directly and indirectly through the influence they exert on the latent part. The seller knows the connection structure of neither the observable nor the latent part of the network. We investigate how the seller can use the available data to estimate the matrix that captures the dependence of observable agents' consumption decisions on the prices offered to them. We provide an algorithm for estimating this matrix under an approximate sparsity condition, and obtain convergence rates for the proposed estimator despite the high-dimensionality that allows more agents than observations. Importantly, we then show that this approximate sparsity condition holds under standard conditions present in the literature and hence our algorithms are applicable to a large class of networks. We establish that by using the estimated matrix the seller can construct prices that lead to a small revenue loss relative to revenue-maximizing prices under complete information, and the optimality gap vanishes relative to the size of the network. We also illustrate that the presence of latent agents leads to significant changes in the structure of the revenue-maximizing prices.