Drift Control of High-Dimensional RBM: A Computational Method Based on Neural Networks
Paper and Code
Sep 20, 2023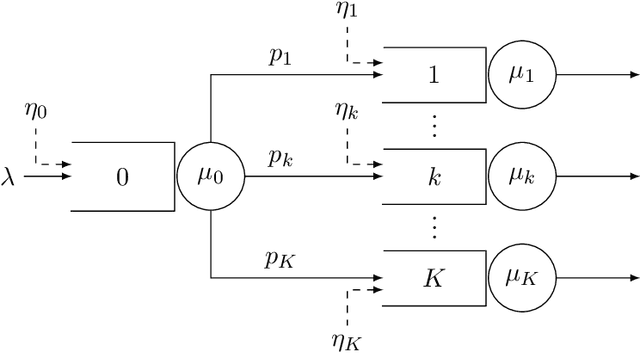
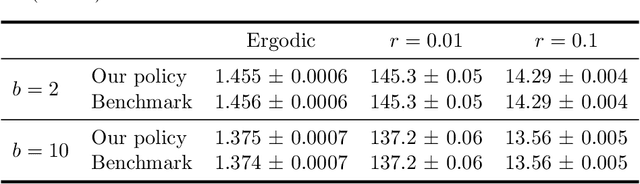
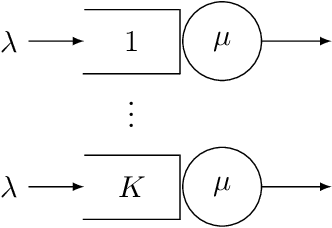
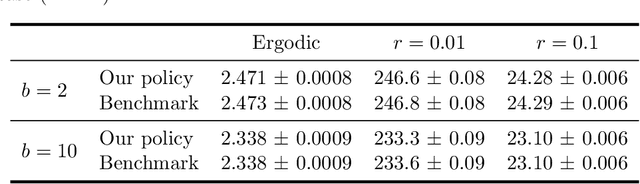
Motivated by applications in queueing theory, we consider a stochastic control problem whose state space is the $d$-dimensional positive orthant. The controlled process $Z$ evolves as a reflected Brownian motion whose covariance matrix is exogenously specified, as are its directions of reflection from the orthant's boundary surfaces. A system manager chooses a drift vector $\theta(t)$ at each time $t$ based on the history of $Z$, and the cost rate at time $t$ depends on both $Z(t)$ and $\theta(t)$. In our initial problem formulation, the objective is to minimize expected discounted cost over an infinite planning horizon, after which we treat the corresponding ergodic control problem. Extending earlier work by Han et al. (Proceedings of the National Academy of Sciences, 2018, 8505-8510), we develop and illustrate a simulation-based computational method that relies heavily on deep neural network technology. For test problems studied thus far, our method is accurate to within a fraction of one percent, and is computationally feasible in dimensions up to at least $d=30$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge