A Drug Recommendation System for cancer cell lines

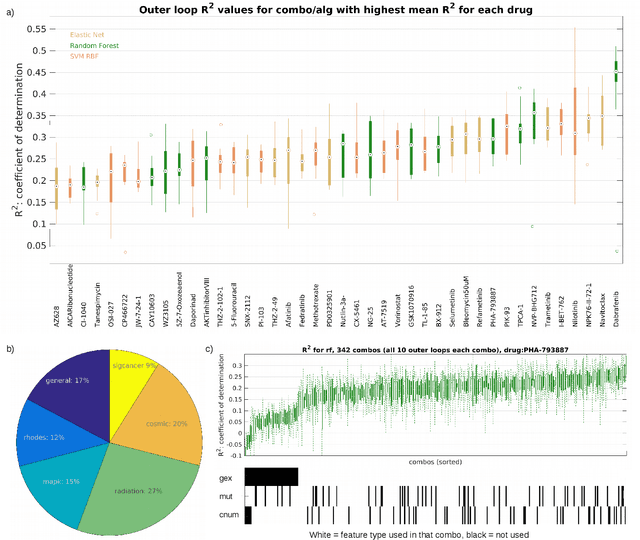
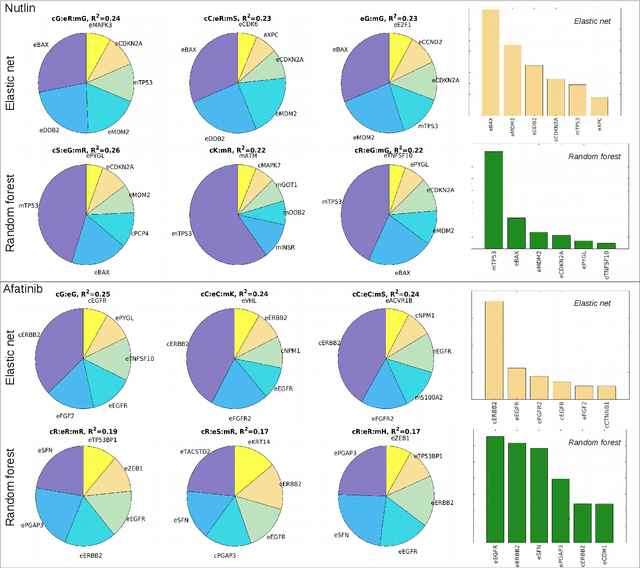
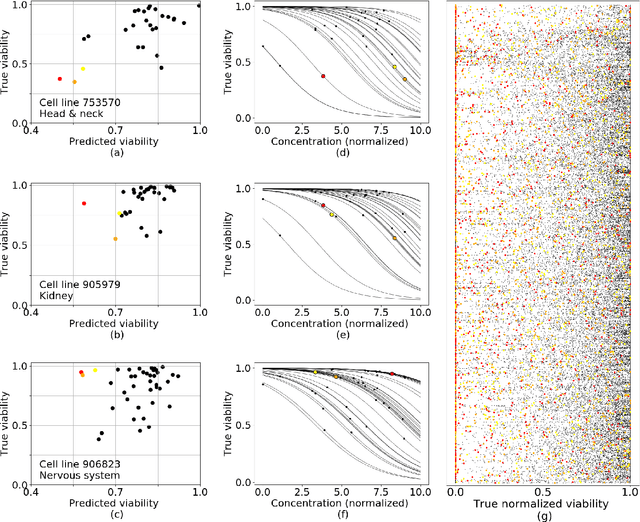
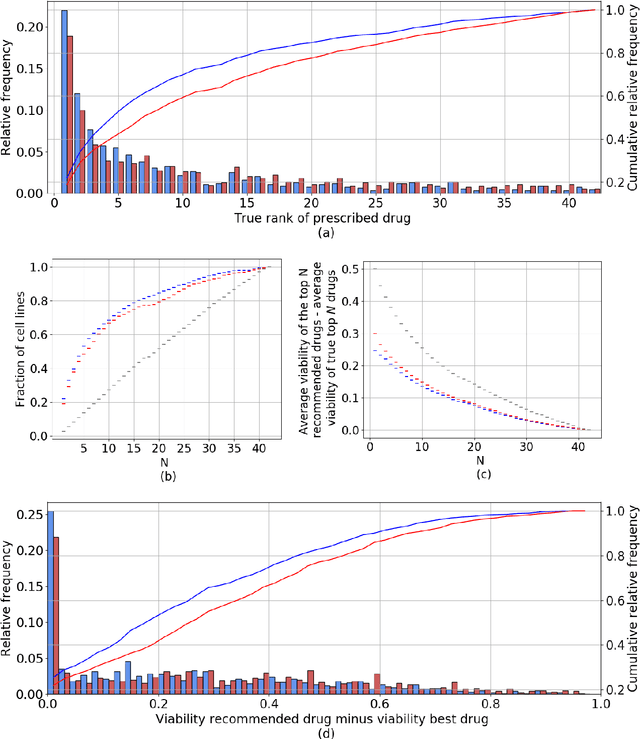
Personalizing drug prescriptions in cancer care based on genomic information requires associating genomic markers with treatment effects. This is an unsolved challenge requiring genomic patient data in yet unavailable volumes as well as appropriate quantitative methods. We attempt to solve this challenge for an experimental proxy for which sufficient data is available: 42 drugs tested on 1018 cancer cell lines. Our goal is to develop a method to identify the drug that is most promising based on a cell line's genomic information. For this, we need to identify for each drug the machine learning method, choice of hyperparameters and genomic features for optimal predictive performance. We extensively compare combinations of gene sets (both curated and random), genetic features, and machine learning algorithms for all 42 drugs. For each drug, the best performing combination (considering only the curated gene sets) is selected. We use these top model parameters for each drug to build and demonstrate a Drug Recommendation System (Dr.S). Insights resulting from this analysis are formulated as best practices for developing drug recommendation systems. The complete software system, called the Cell Line Analyzer, is written in Python and available on github.

An image representation based convolutional network for DNA classification

The folding structure of the DNA molecule combined with helper molecules, also referred to as the chromatin, is highly relevant for the functional properties of DNA. The chromatin structure is largely determined by the underlying primary DNA sequence, though the interaction is not yet fully understood. In this paper we develop a convolutional neural network that takes an image-representation of primary DNA sequence as its input, and predicts key determinants of chromatin structure. The method is developed such that it is capable of detecting interactions between distal elements in the DNA sequence, which are known to be highly relevant. Our experiments show that the method outperforms several existing methods both in terms of prediction accuracy and training time.

Generic identification of binary-valued hidden Markov processes

The generic identification problem is to decide whether a stochastic process $(X_t)$ is a hidden Markov process and if yes to infer its parameters for all but a subset of parametrizations that form a lower-dimensional subvariety in parameter space. Partial answers so far available depend on extra assumptions on the processes, which are usually centered around stationarity. Here we present a general solution for binary-valued hidden Markov processes. Our approach is rooted in algebraic statistics hence it is geometric in nature. We find that the algebraic varieties associated with the probability distributions of binary-valued hidden Markov processes are zero sets of determinantal equations which draws a connection to well-studied objects from algebra. As a consequence, our solution allows for algorithmic implementation based on elementary (linear) algebraic routines.