A Gesture-Based Visual Learning Model for Acoustophoretic Interactions using a Swarm of AcoustoBots

AcoustoBots are mobile acoustophoretic robots capable of delivering mid-air haptics, directional audio, and acoustic levitation, but existing implementations rely on scripted commands and lack an intuitive interface for real-time human control. This work presents a gesture-based visual learning framework for contactless human-swarm interaction with a multimodal AcoustoBot platform. The system combines ESP32-CAM gesture capture, PhaseSpace motion tracking, centralized processing, and an OpenCLIP-based visual learning model (VLM) with linear probing to classify three hand gestures and map them to haptics, audio, and levitation modalities. Validation accuracy improved from about 67% with a small dataset to nearly 98% with the largest dataset. In integrated experiments with two AcoustoBots, the system achieved an overall gesture-to-modality switching accuracy of 87.8% across 90 trials, with an average end-to-end latency of 3.95 seconds. These results demonstrate the feasibility of using a vision-language-model-based gesture interface for multimodal human-swarm interaction. While the current system is limited by centralized processing, a static gesture set, and controlled-environment evaluation, it establishes a foundation for more expressive, scalable, and accessible swarm robotic interfaces.

Action-Based Conversations Dataset: A Corpus for Building More In-Depth Task-Oriented Dialogue Systems

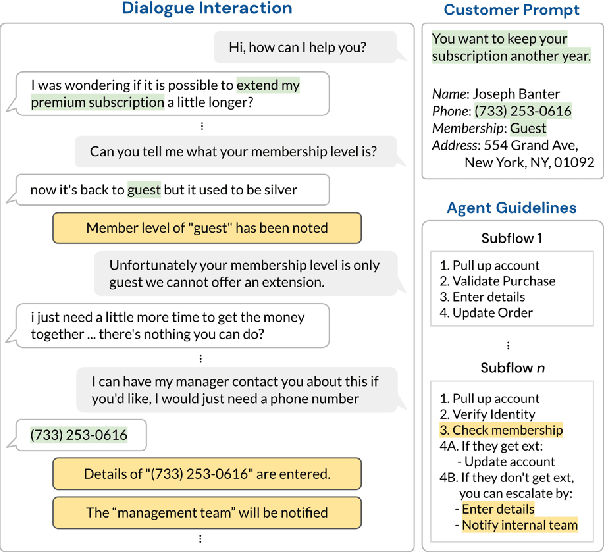
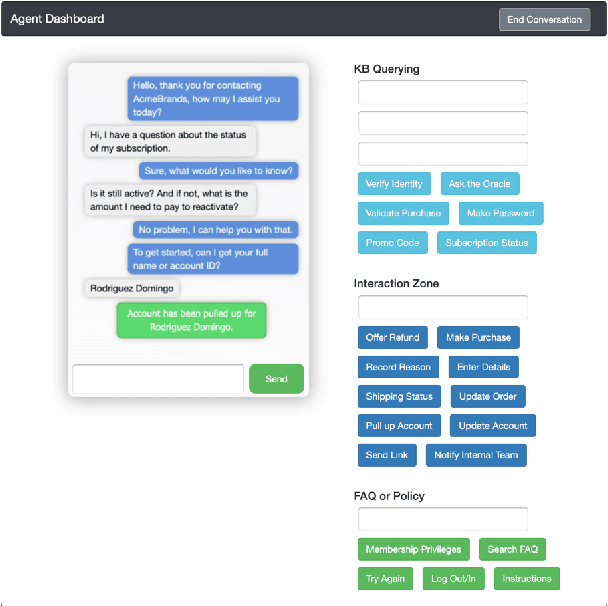
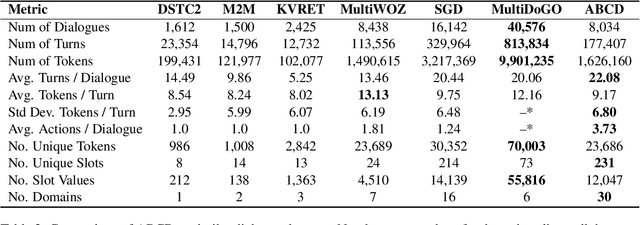
Existing goal-oriented dialogue datasets focus mainly on identifying slots and values. However, customer support interactions in reality often involve agents following multi-step procedures derived from explicitly-defined company policies as well. To study customer service dialogue systems in more realistic settings, we introduce the Action-Based Conversations Dataset (ABCD), a fully-labeled dataset with over 10K human-to-human dialogues containing 55 distinct user intents requiring unique sequences of actions constrained by policies to achieve task success. We propose two additional dialog tasks, Action State Tracking and Cascading Dialogue Success, and establish a series of baselines involving large-scale, pre-trained language models on this dataset. Empirical results demonstrate that while more sophisticated networks outperform simpler models, a considerable gap (50.8% absolute accuracy) still exists to reach human-level performance on ABCD.

Laplacian Smoothing Gradient Descent

We propose a very simple modification of gradient descent and stochastic gradient descent. We show that when applied to a variety of machine learning models including softmax regression, convolutional neural nets, generative adversarial nets, and deep reinforcement learning, this very simple surrogate can dramatically reduce the variance and improve the accuracy of the generalization. The new algorithm, (which depends on one nonnegative parameter) when applied to non-convex minimization, tends to avoid sharp local minima. Instead it seeks somewhat flatter local (and often global) minima. The method only involves preconditioning the gradient by the inverse of a tri-diagonal matrix that is positive definite. The motivation comes from the theory of Hamilton-Jacobi partial differential equations. This theory demonstrates that the new algorithm is almost the same as doing gradient descent on a new function which (a) has the same global minima as the original function and (b) is "more convex". Again, the programming effort in doing this is minimal, in cost, complexity and effort. We implement our algorithm into both PyTorch and Tensorflow platforms, which will be made publicly available.