Learning to quantify graph nodes

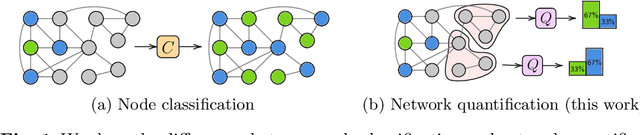
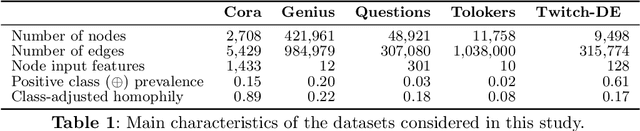
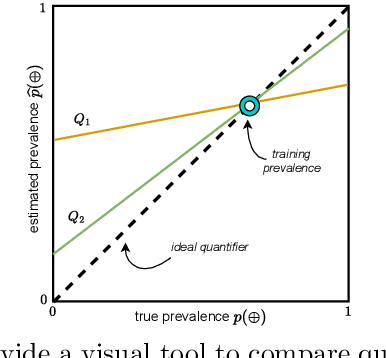
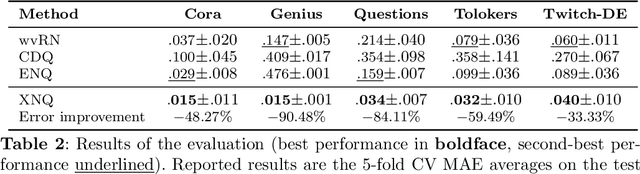
Network Quantification is the problem of estimating the class proportions in unlabeled subsets of graph nodes. When prior probability shift is at play, this task cannot be effectively addressed by first classifying the nodes and then counting the class predictions. In addition, unlike non-relational quantification on i.i.d. datapoints, Network Quantification demands enhanced flexibility to capture a broad range of connectivity patterns, resilience to the challenge of heterophily, and efficiency to scale to larger networks. To meet these stringent requirements we introduce XNQ, a novel method that synergizes the flexibility and efficiency of the unsupervised node embeddings computed by randomized recursive Graph Neural Networks, with an Expectation-Maximization algorithm that provides a robust quantification-aware adjustment to the output probabilities of a calibrated node classifier. We validate the design choices underpinning our method through comprehensive ablation experiments. In an extensive evaluation, we find that our approach consistently and significantly improves on the best Network Quantification methods to date, thereby setting the new state of the art for this challenging task. Simultaneously, it provides a training speed-up of up to 10x-100x over other graph learning based methods.

Modeling Edge Features with Deep Bayesian Graph Networks

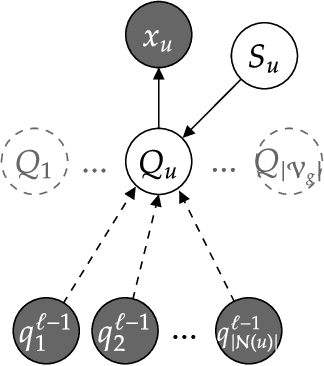
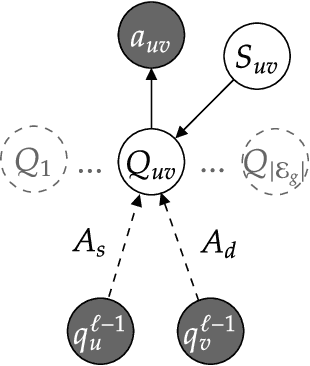
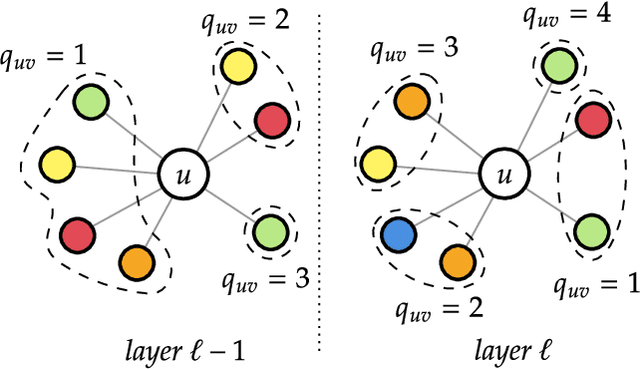
We propose an extension of the Contextual Graph Markov Model, a deep and probabilistic machine learning model for graphs, to model the distribution of edge features. Our approach is architectural, as we introduce an additional Bayesian network mapping edge features into discrete states to be used by the original model. In doing so, we are also able to build richer graph representations even in the absence of edge features, which is confirmed by the performance improvements on standard graph classification benchmarks. Moreover, we successfully test our proposal in a graph regression scenario where edge features are of fundamental importance, and we show that the learned edge representation provides substantial performance improvements against the original model on three link prediction tasks. By keeping the computational complexity linear in the number of edges, the proposed model is amenable to large-scale graph processing.

Is Rewiring Actually Helpful in Graph Neural Networks?

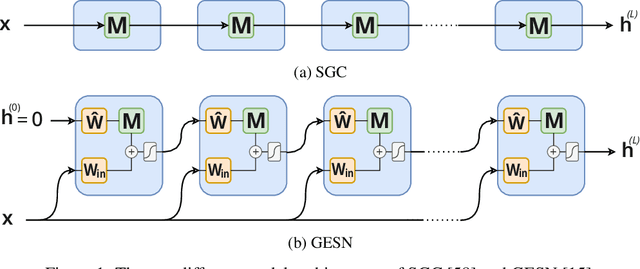
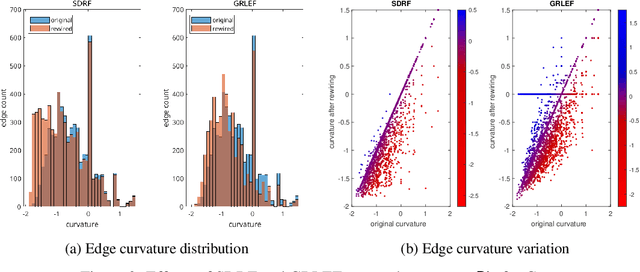
Graph neural networks compute node representations by performing multiple message-passing steps that consist in local aggregations of node features. Having deep models that can leverage longer-range interactions between nodes is hindered by the issues of over-smoothing and over-squashing. In particular, the latter is attributed to the graph topology which guides the message-passing, causing a node representation to become insensitive to information contained at distant nodes. Many graph rewiring methods have been proposed to remedy or mitigate this problem. However, properly evaluating the benefits of these methods is made difficult by the coupling of over-squashing with other issues strictly related to model training, such as vanishing gradients. Therefore, we propose an evaluation setting based on message-passing models that do not require training to compute node and graph representations. We perform a systematic experimental comparison on real-world node and graph classification tasks, showing that rewiring the underlying graph rarely does confer a practical benefit for message-passing.

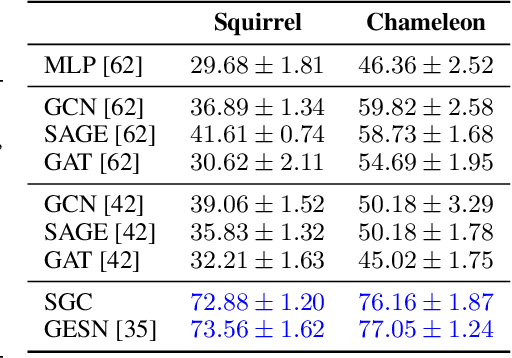
Addressing Heterophily in Node Classification with Graph Echo State Networks

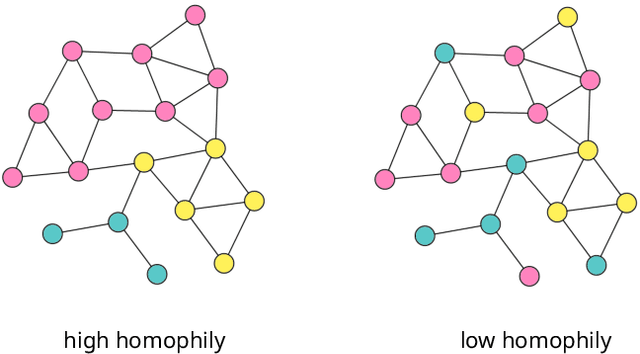
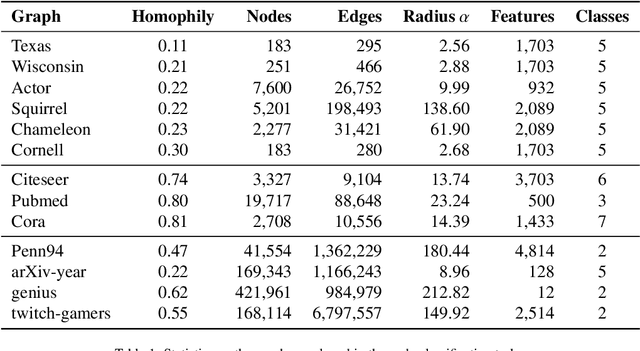
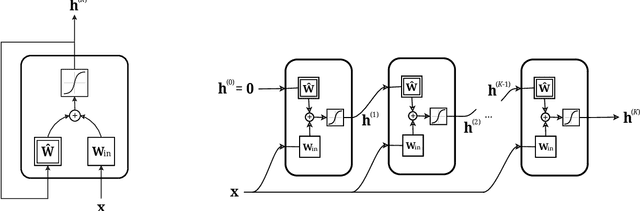
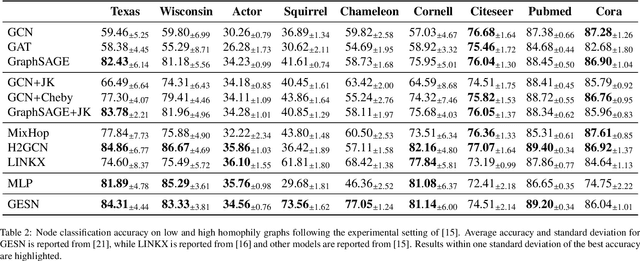
Node classification tasks on graphs are addressed via fully-trained deep message-passing models that learn a hierarchy of node representations via multiple aggregations of a node's neighbourhood. While effective on graphs that exhibit a high ratio of intra-class edges, this approach poses challenges in the opposite case, i.e. heterophily, where nodes belonging to the same class are usually further apart. In graphs with a high degree of heterophily, the smoothed representations based on close neighbours computed by convolutional models are no longer effective. So far, architectural variations in message-passing models to reduce excessive smoothing or rewiring the input graph to improve longer-range message passing have been proposed. In this paper, we address the challenges of heterophilic graphs with Graph Echo State Network (GESN) for node classification. GESN is a reservoir computing model for graphs, where node embeddings are recursively computed by an untrained message-passing function. Our experiments show that reservoir models are able to achieve better or comparable accuracy with respect to most fully trained deep models that implement ad hoc variations in the architectural bias or perform rewiring as a preprocessing step on the input graph, with an improvement in terms of efficiency/accuracy trade-off. Furthermore, our analysis shows that GESN is able to effectively encode the structural relationships of a graph node, by showing a correlation between iterations of the recursive embedding function and the distribution of shortest paths in a graph.

Leave Graphs Alone: Addressing Over-Squashing without Rewiring

Recent works have investigated the role of graph bottlenecks in preventing long-range information propagation in message-passing graph neural networks, causing the so-called `over-squashing' phenomenon. As a remedy, graph rewiring mechanisms have been proposed as preprocessing steps. Graph Echo State Networks (GESNs) are a reservoir computing model for graphs, where node embeddings are recursively computed by an untrained message-passing function. In this paper, we show that GESNs can achieve a significantly better accuracy on six heterophilic node classification tasks without altering the graph connectivity, thus suggesting a different route for addressing the over-squashing problem.

Beyond Homophily with Graph Echo State Networks

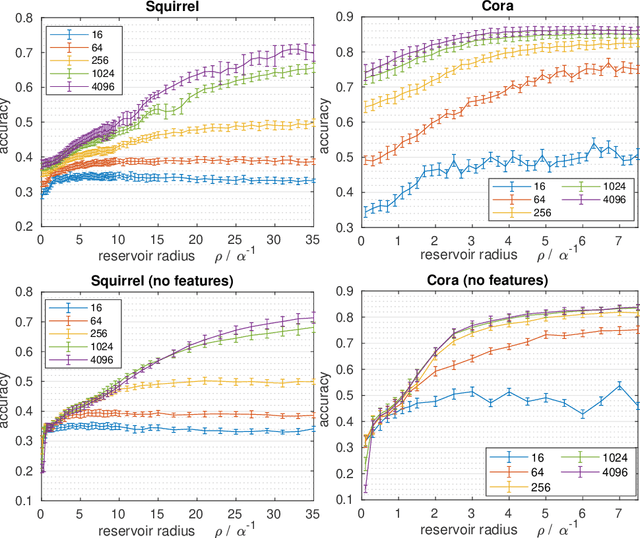
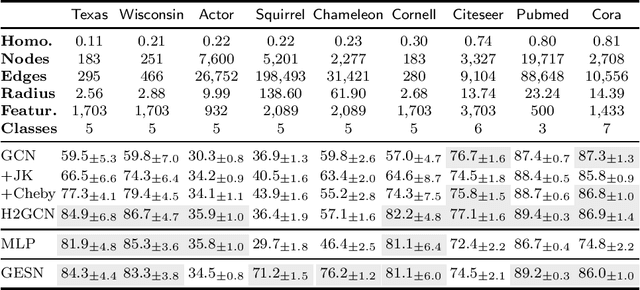
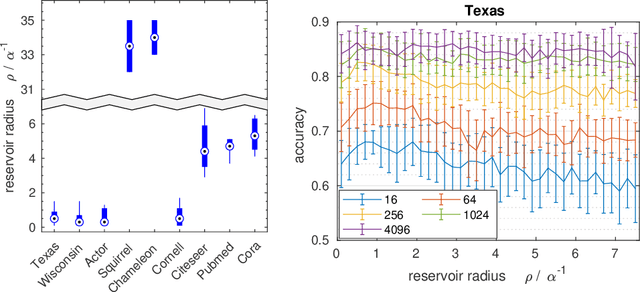
Graph Echo State Networks (GESN) have already demonstrated their efficacy and efficiency in graph classification tasks. However, semi-supervised node classification brought out the problem of over-smoothing in end-to-end trained deep models, which causes a bias towards high homophily graphs. We evaluate for the first time GESN on node classification tasks with different degrees of homophily, analyzing also the impact of the reservoir radius. Our experiments show that reservoir models are able to achieve better or comparable accuracy with respect to fully trained deep models that implement ad hoc variations in the architectural bias, with a gain in terms of efficiency.

Dynamic Graph Echo State Networks

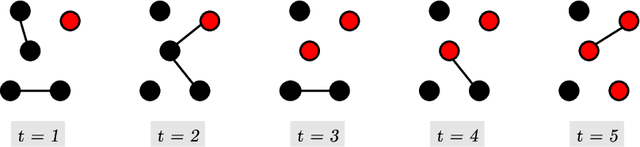
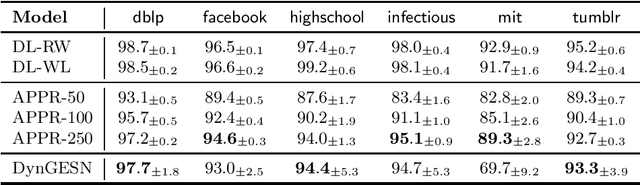
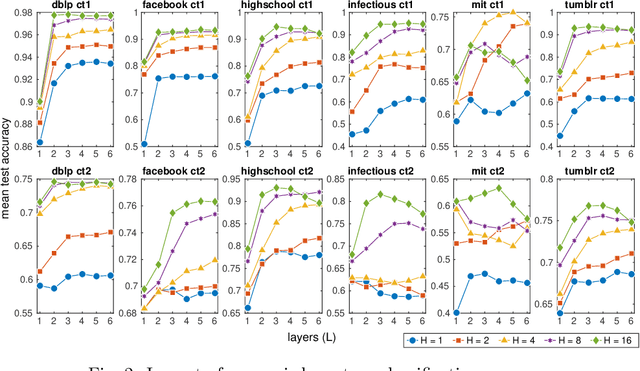
Dynamic temporal graphs represent evolving relations between entities, e.g. interactions between social network users or infection spreading. We propose an extension of graph echo state networks for the efficient processing of dynamic temporal graphs, with a sufficient condition for their echo state property, and an experimental analysis of reservoir layout impact. Compared to temporal graph kernels that need to hold the entire history of vertex interactions, our model provides a vector encoding for the dynamic graph that is updated at each time-step without requiring training. Experiments show accuracy comparable to approximate temporal graph kernels on twelve dissemination process classification tasks.

TEACHING -- Trustworthy autonomous cyber-physical applications through human-centred intelligence

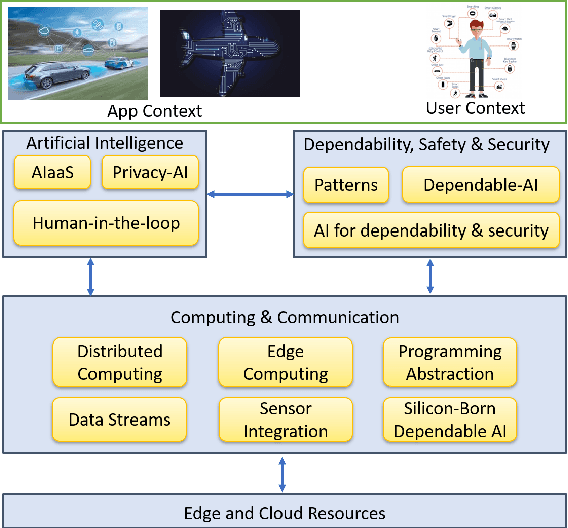
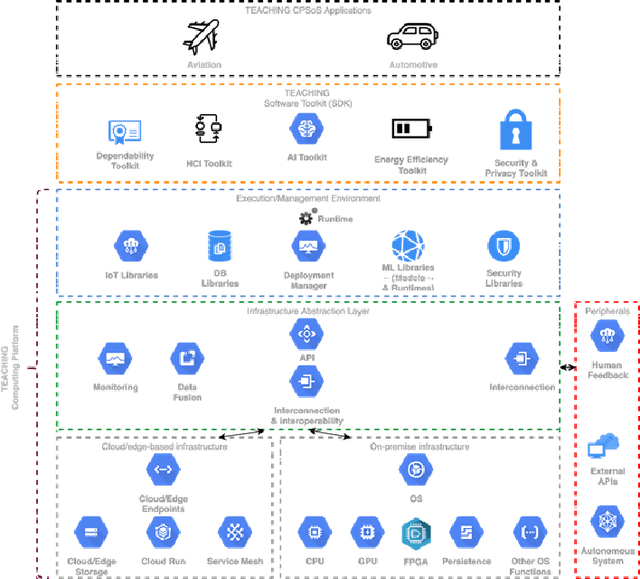
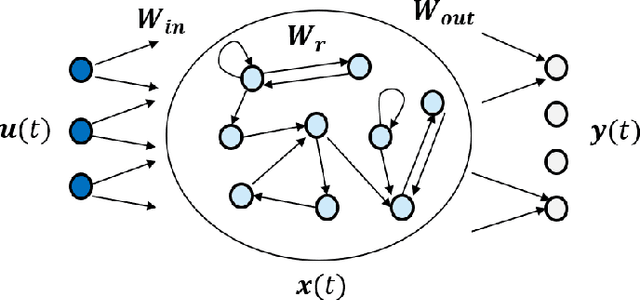
This paper discusses the perspective of the H2020 TEACHING project on the next generation of autonomous applications running in a distributed and highly heterogeneous environment comprising both virtual and physical resources spanning the edge-cloud continuum. TEACHING puts forward a human-centred vision leveraging the physiological, emotional, and cognitive state of the users as a driver for the adaptation and optimization of the autonomous applications. It does so by building a distributed, embedded and federated learning system complemented by methods and tools to enforce its dependability, security and privacy preservation. The paper discusses the main concepts of the TEACHING approach and singles out the main AI-related research challenges associated with it. Further, we provide a discussion of the design choices for the TEACHING system to tackle the aforementioned challenges

Phase Transition Adaptation

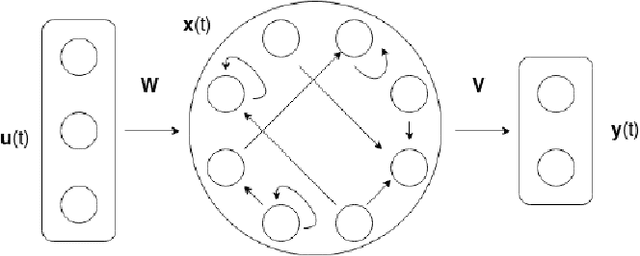
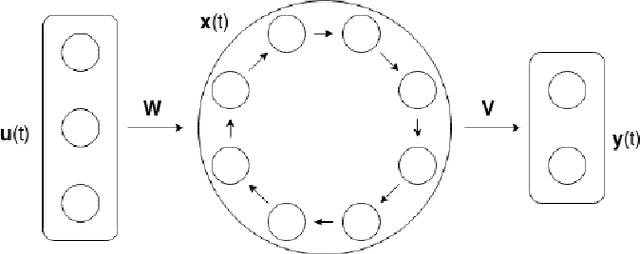
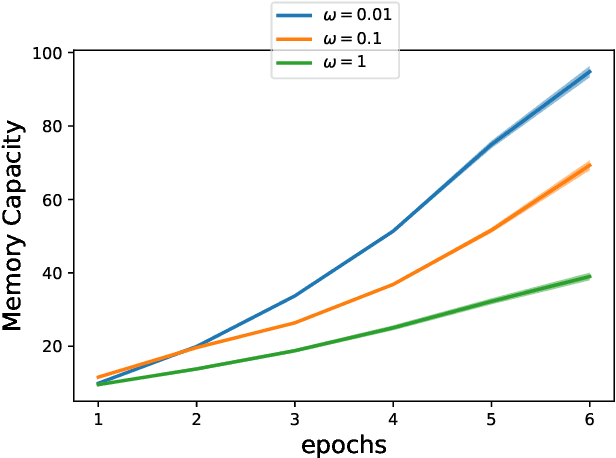
Artificial Recurrent Neural Networks are a powerful information processing abstraction, and Reservoir Computing provides an efficient strategy to build robust implementations by projecting external inputs into high dimensional dynamical system trajectories. In this paper, we propose an extension of the original approach, a local unsupervised learning mechanism we call Phase Transition Adaptation, designed to drive the system dynamics towards the `edge of stability'. Here, the complex behavior exhibited by the system elicits an enhancement in its overall computational capacity. We show experimentally that our approach consistently achieves its purpose over several datasets.

Pyramidal Reservoir Graph Neural Network

We propose a deep Graph Neural Network (GNN) model that alternates two types of layers. The first type is inspired by Reservoir Computing (RC) and generates new vertex features by iterating a non-linear map until it converges to a fixed point. The second type of layer implements graph pooling operations, that gradually reduce the support graph and the vertex features, and further improve the computational efficiency of the RC-based GNN. The architecture is, therefore, pyramidal. In the last layer, the features of the remaining vertices are combined into a single vector, which represents the graph embedding. Through a mathematical derivation introduced in this paper, we show formally how graph pooling can reduce the computational complexity of the model and speed-up the convergence of the dynamical updates of the vertex features. Our proposed approach to the design of RC-based GNNs offers an advantageous and principled trade-off between accuracy and complexity, which we extensively demonstrate in experiments on a large set of graph datasets.