Modeling Edge Features with Deep Bayesian Graph Networks
Paper and Code
Aug 17, 2023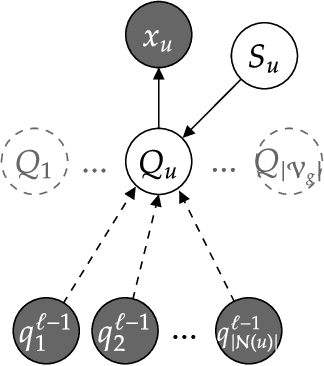
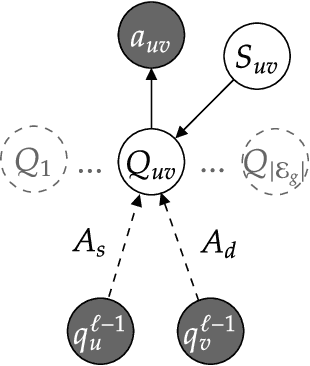
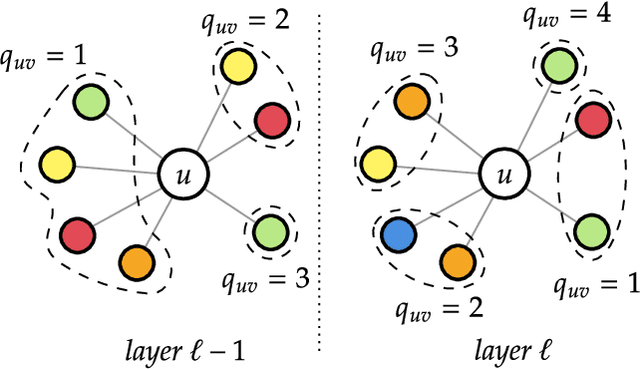
We propose an extension of the Contextual Graph Markov Model, a deep and probabilistic machine learning model for graphs, to model the distribution of edge features. Our approach is architectural, as we introduce an additional Bayesian network mapping edge features into discrete states to be used by the original model. In doing so, we are also able to build richer graph representations even in the absence of edge features, which is confirmed by the performance improvements on standard graph classification benchmarks. Moreover, we successfully test our proposal in a graph regression scenario where edge features are of fundamental importance, and we show that the learned edge representation provides substantial performance improvements against the original model on three link prediction tasks. By keeping the computational complexity linear in the number of edges, the proposed model is amenable to large-scale graph processing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge