Coded Matrix Computations for D2D-enabled Linearized Federated Learning

Federated learning (FL) is a popular technique for training a global model on data distributed across client devices. Like other distributed training techniques, FL is susceptible to straggler (slower or failed) clients. Recent work has proposed to address this through device-to-device (D2D) offloading, which introduces privacy concerns. In this paper, we propose a novel straggler-optimal approach for coded matrix computations which can significantly reduce the communication delay and privacy issues introduced from D2D data transmissions in FL. Moreover, our proposed approach leads to a considerable improvement of the local computation speed when the generated data matrix is sparse. Numerical evaluations confirm the superiority of our proposed method over baseline approaches.

Efficient Detection and Filtering Systems for Distributed Training

A plethora of modern machine learning tasks requires the utilization of large-scale distributed clusters as a critical component of the training pipeline. However, abnormal Byzantine behavior of the worker nodes can derail the training and compromise the quality of the inference. Such behavior can be attributed to unintentional system malfunctions or orchestrated attacks; as a result, some nodes may return arbitrary results to the parameter server (PS) that coordinates the training. Recent work considers a wide range of attack models and has explored robust aggregation and/or computational redundancy to correct the distorted gradients. In this work, we consider attack models ranging from strong ones: $q$ omniscient adversaries with full knowledge of the defense protocol that can change from iteration to iteration to weak ones: $q$ randomly chosen adversaries with limited collusion abilities that only change every few iterations at a time. Our algorithms rely on redundant task assignments coupled with detection of adversarial behavior. For strong attacks, we demonstrate a reduction in the fraction of distorted gradients ranging from 16%-99% as compared to the prior state-of-the-art. Our top-1 classification accuracy results on the CIFAR-10 data set demonstrate a 25% advantage in accuracy (averaged over strong and weak scenarios) under the most sophisticated attacks compared to state-of-the-art methods.

Aspis: A Robust Detection System for Distributed Learning

State of the art machine learning models are routinely trained on large scale distributed clusters. Crucially, such systems can be compromised when some of the computing devices exhibit abnormal (Byzantine) behavior and return arbitrary results to the parameter server (PS). This behavior may be attributed to a plethora of reasons including system failures and orchestrated attacks. Existing work suggests robust aggregation and/or computational redundancy to alleviate the effect of distorted gradients. However, most of these schemes are ineffective when an adversary knows the task assignment and can judiciously choose the attacked workers to induce maximal damage. Our proposed method Aspis assigns gradient computations to worker nodes using a subset-based assignment which allows for multiple consistency checks on the behavior of a worker node. Examination of the calculated gradients and post-processing (clique-finding in an appropriately constructed graph) by the central node allows for efficient detection and subsequent exclusion of adversaries from the training process. We prove the Byzantine resilience and detection guarantees of Aspis under weak and strong attacks and extensively evaluate the system on various large-scale training scenarios. The main metric for our experiments is the test accuracy for which we demonstrate significant improvement of about 30% compared to many state-of-the-art approaches on the CIFAR-10 dataset. The corresponding reduction of the fraction of corrupted gradients ranges from 16% to 98%.

ByzShield: An Efficient and Robust System for Distributed Training

Training of large scale models on distributed clusters is a critical component of the machine learning pipeline. However, this training can easily be made to fail if some workers behave in an adversarial (Byzantine) fashion whereby they return arbitrary results to the parameter server (PS). A plethora of existing papers consider a variety of attack models and propose robust aggregation and/or computational redundancy to alleviate the effects of these attacks. In this work we consider an omniscient attack model where the adversary has full knowledge about the gradient computation assignments of the workers and can choose to attack (up to) any q out of n worker nodes to induce maximal damage. Our redundancy-based method ByzShield leverages the properties of bipartite expander graphs for the assignment of tasks to workers; this helps to effectively mitigate the effect of the Byzantine behavior. Specifically, we demonstrate an upper bound on the worst case fraction of corrupted gradients based on the eigenvalues of our constructions which are based on mutually orthogonal Latin squares and Ramanujan graphs. Our numerical experiments indicate over a 36% reduction on average in the fraction of corrupted gradients compared to the state of the art. Likewise, our experiments on training followed by image classification on the CIFAR-10 dataset show that ByzShield has on average a 20% advantage in accuracy under the most sophisticated attacks. ByzShield also tolerates a much larger fraction of adversarial nodes compared to prior work.

Federated Over-the-Air Subspace Learning from Incomplete Data

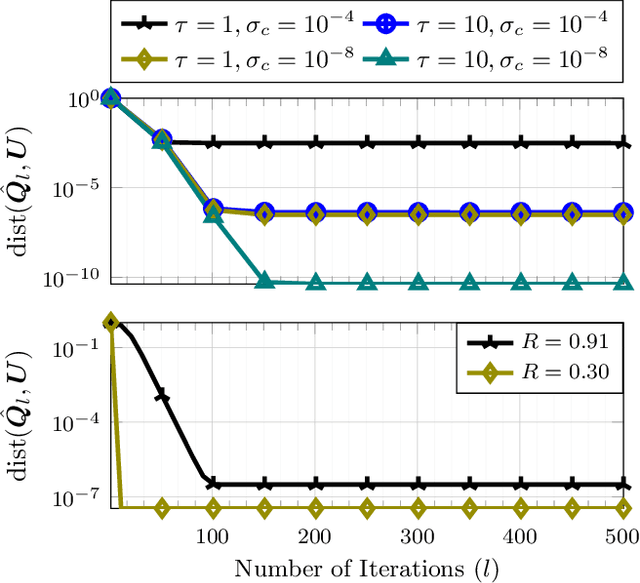
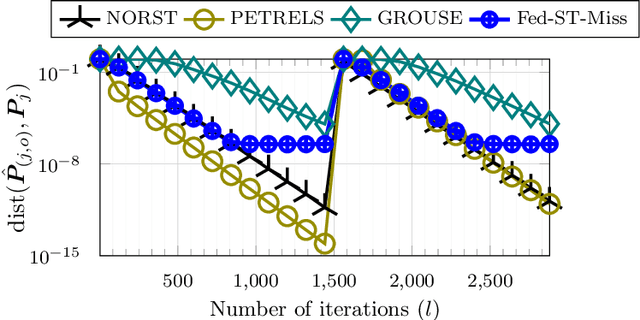
Federated learning refers to a distributed learning scenario in which users/nodes keep their data private but only share intermediate locally computed iterates with the master node. The master, in turn, shares a global aggregate of these iterates with all the nodes at each iteration. In this work, we consider a wireless federated learning scenario where the nodes communicate to and from the master node via a wireless channel. Current and upcoming technologies such as 5G (and beyond) will operate mostly in a non-orthogonal multiple access (NOMA) mode where transmissions from the users occupy the same bandwidth and interfere at the access point. These technologies naturally lend themselves to an "over-the-air" superposition whereby information received from the user nodes can be directly summed at the master node. However, over-the-air aggregation also means that the channel noise can corrupt the algorithm iterates at the time of aggregation at the master. This iteration noise introduces a novel set of challenges that have not been previously studied in the literature. It needs to be treated differently from the well-studied setting of noise or corruption in the dataset itself. In this work, we first study the subspace learning problem in a federated over-the-air setting. Subspace learning involves computing the subspace spanned by the top $r$ singular vectors of a given matrix. We develop a federated over-the-air version of the power method (FedPM) and show that its iterates converge as long as (i) the channel noise is very small compared to the $r$-th singular value of the matrix; and (ii) the ratio between its $(r+1)$-th and $r$-th singular value is smaller than a constant less than one. The second important contribution of this work is to show how over-the-air FedPM can be used to obtain a provably accurate federated solution for subspace tracking in the presence of missing data.

Resolvable Designs for Speeding up Distributed Computing

Distributed computing frameworks such as MapReduce are often used to process large computational jobs. They operate by partitioning each job into smaller tasks executed on different servers. The servers also need to exchange intermediate values to complete the computation. Experimental evidence suggests that this so-called Shuffle phase can be a significant part of the overall execution time for several classes of jobs. Prior work has demonstrated a natural tradeoff between computation and communication whereby running redundant copies of jobs can reduce the Shuffle traffic load, thereby leading to reduced overall execution times. For a single job, the main drawback of this approach is that it requires the original job to be split into a number of files that grows exponentially in the system parameters. When extended to multiple jobs (with specific function types), these techniques suffer from a limitation of a similar flavor, i.e., they require an exponentially large number of jobs to be executed. In practical scenarios, these requirements can significantly reduce the promised gains of the method. In this work, we show that a class of combinatorial structures called resolvable designs can be used to develop efficient coded distributed computing schemes for both the single and multiple job scenarios considered in prior work. We present both theoretical analysis and exhaustive experimental results (on Amazon EC2 clusters) that demonstrate the performance advantages of our method. For the single and multiple job cases, we obtain speed-ups of 4.69x (and 2.6x over prior work) and 4.31x over the baseline approach, respectively.

CAMR: Coded Aggregated MapReduce

Many big data algorithms executed on MapReduce-like systems have a shuffle phase that often dominates the overall job execution time. Recent work has demonstrated schemes where the communication load in the shuffle phase can be traded off for the computation load in the map phase. In this work, we focus on a class of distributed algorithms, broadly used in deep learning, where intermediate computations of the same task can be combined. Even though prior techniques reduce the communication load significantly, they require a number of jobs that grows exponentially in the system parameters. This limitation is crucial and may diminish the load gains as the algorithm scales. We propose a new scheme which achieves the same load as the state-of-the-art while ensuring that the number of jobs as well as the number of subfiles that the data set needs to be split into remain small.

Erasure coding for distributed matrix multiplication for matrices with bounded entries

Distributed matrix multiplication is widely used in several scientific domains. It is well recognized that computation times on distributed clusters are often dominated by the slowest workers (called stragglers). Recent work has demonstrated that straggler mitigation can be viewed as a problem of designing erasure codes. For matrices $\mathbf A$ and $\mathbf B$, the technique essentially maps the computation of $\mathbf A^T \mathbf B$ into the multiplication of smaller (coded) submatrices. The stragglers are treated as erasures in this process. The computation can be completed as long as a certain number of workers (called the recovery threshold) complete their assigned tasks. We present a novel coding strategy for this problem when the absolute values of the matrix entries are sufficiently small. We demonstrate a tradeoff between the assumed absolute value bounds on the matrix entries and the recovery threshold. At one extreme, we are optimal with respect to the recovery threshold and on the other extreme, we match the threshold of prior work. Experimental results on cloud-based clusters validate the benefits of our method.