Praneeth Narayanamurthy
Matrix Approximation with Side Information: When Column Sampling is Enough
Dec 11, 2022Abstract:A novel matrix approximation problem is considered herein: observations based on a few fully sampled columns and quasi-polynomial structural side information are exploited. The framework is motivated by quantum chemistry problems wherein full matrix computation is expensive, and partial computations only lead to column information. The proposed algorithm successfully estimates the column and row-space of a true matrix given a priori structural knowledge of the true matrix. A theoretical spectral error bound is provided, which captures the possible inaccuracies of the side information. The error bound proves it scales in its signal-to-noise (SNR) ratio. The proposed algorithm is validated via simulations which enable the characterization of the amount of information provided by the quasi-polynomial side information.
Uncertainty-Based Non-Parametric Active Peak Detection
May 05, 2022

Abstract:Active, non-parametric peak detection is considered. As a use case, active source localization is examined and an uncertainty-based sampling scheme algorithm to effectively localize the peak from a few energy measurements is designed. It is shown that under very mild conditions, the source localization error with $m$ actively chosen energy measurements scales as $O(\log^2 m/m)$. Numerically, it is shown that in low-sample regimes, the proposed method enjoys superior performance on several types of data and outperforms the state-of-the-art passive source localization approaches and in the low sample regime, can outperform greedy methods as well.
Fast Robust Subspace Tracking via PCA in Sparse Data-Dependent Noise
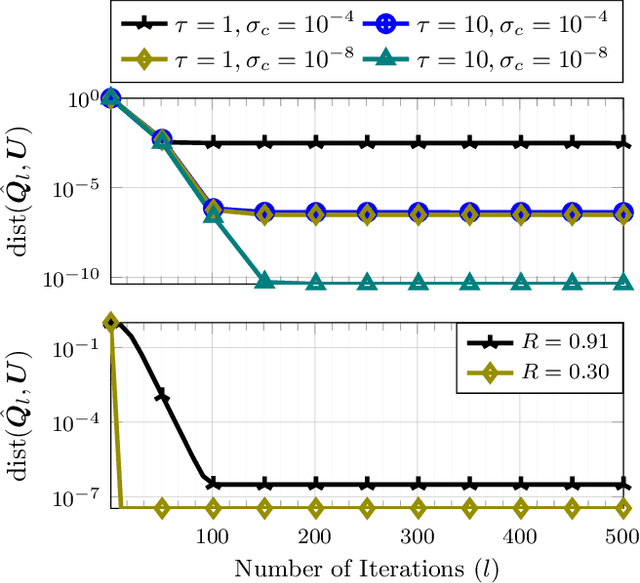
Jun 14, 2020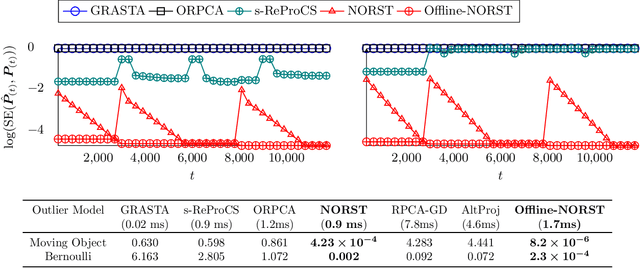
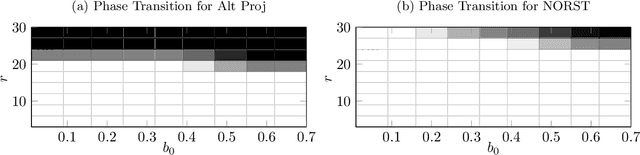
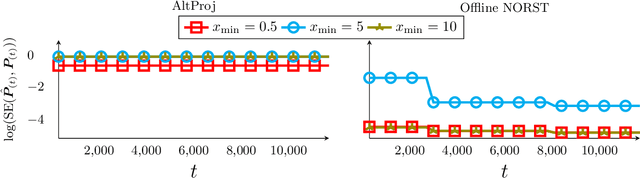

Abstract:This work studies the robust subspace tracking (ST) problem. Robust ST can be simply understood as a (slow) time-varying subspace extension of robust PCA. It assumes that the true data lies in a low-dimensional subspace that is either fixed or changes slowly with time. The goal is to track the changing subspaces over time in the presence of additive sparse outliers and to do this quickly (with a short delay). We introduce a ``fast'' mini-batch robust ST solution that is provably correct under mild assumptions. Here ``fast'' means two things: (i) the subspace changes can be detected and the subspaces can be tracked with near-optimal delay, and (ii) the time complexity of doing this is the same as that of simple (non-robust) PCA. Our main result assumes piecewise constant subspaces (needed for identifiability), but we also provide a corollary for the case when there is a little change at each time. A second contribution is a novel non-asymptotic guarantee for PCA in linearly data-dependent noise. An important setting where this result is useful is for linearly data-dependent noise that is sparse with enough support changes over time. The subspace update step of our proposed robust ST solution uses this result.
Federated Over-the-Air Subspace Learning from Incomplete Data
Feb 28, 2020
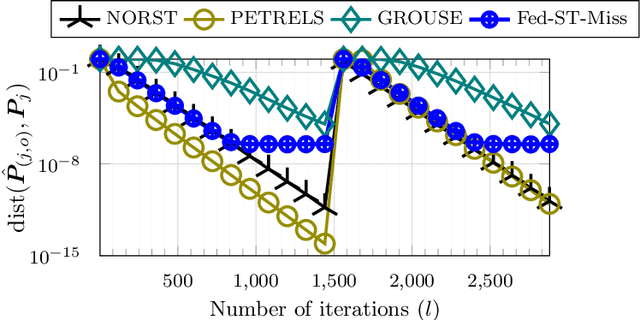
Abstract:Federated learning refers to a distributed learning scenario in which users/nodes keep their data private but only share intermediate locally computed iterates with the master node. The master, in turn, shares a global aggregate of these iterates with all the nodes at each iteration. In this work, we consider a wireless federated learning scenario where the nodes communicate to and from the master node via a wireless channel. Current and upcoming technologies such as 5G (and beyond) will operate mostly in a non-orthogonal multiple access (NOMA) mode where transmissions from the users occupy the same bandwidth and interfere at the access point. These technologies naturally lend themselves to an "over-the-air" superposition whereby information received from the user nodes can be directly summed at the master node. However, over-the-air aggregation also means that the channel noise can corrupt the algorithm iterates at the time of aggregation at the master. This iteration noise introduces a novel set of challenges that have not been previously studied in the literature. It needs to be treated differently from the well-studied setting of noise or corruption in the dataset itself. In this work, we first study the subspace learning problem in a federated over-the-air setting. Subspace learning involves computing the subspace spanned by the top $r$ singular vectors of a given matrix. We develop a federated over-the-air version of the power method (FedPM) and show that its iterates converge as long as (i) the channel noise is very small compared to the $r$-th singular value of the matrix; and (ii) the ratio between its $(r+1)$-th and $r$-th singular value is smaller than a constant less than one. The second important contribution of this work is to show how over-the-air FedPM can be used to obtain a provably accurate federated solution for subspace tracking in the presence of missing data.
Phaseless Low Rank Matrix Recovery and Subspace Tracking
Feb 13, 2019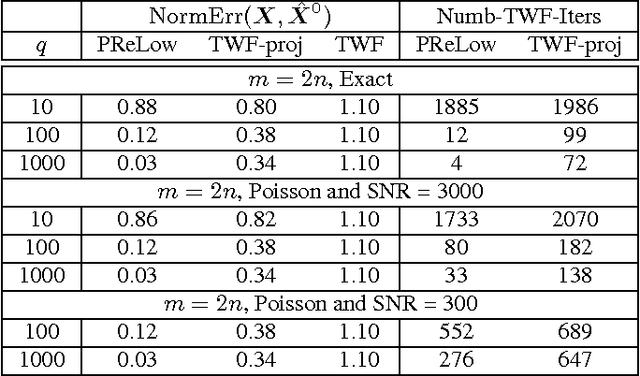
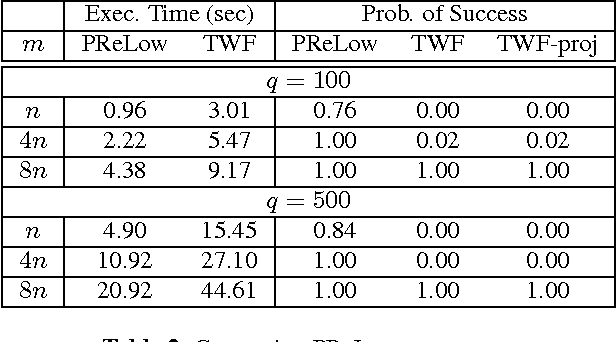
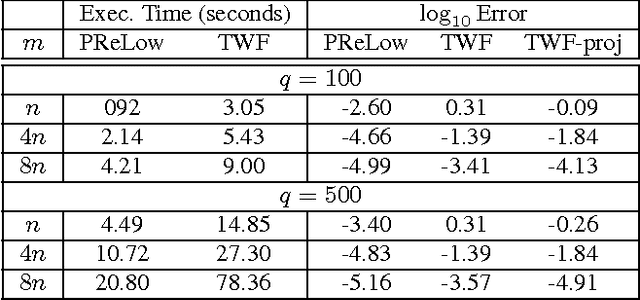
Abstract:This work introduces the first simple and provably correct solution for recovering a low-rank matrix from phaseless (magnitude-only) linear projections of each of its columns. This problem finds important applications in phaseless dynamic imaging, e.g., Fourier ptychographic imaging of live biological specimens. We demonstrate the practical advantage of our proposed approach, AltMinLowRaP, over existing work via extensive simulation, and some real-data, experiments. Under a right incoherence (denseness of right singular vectors) assumption, our guarantee shows that, in the regime of small ranks, r, the sample complexity of AltMinLowRaP is much smaller than what standard phase retrieval methods need; and it is only $r^3$ times the order-optimal complexity for low-rank matrix recovery. We also provide a solution for a dynamic extension of the above problem. This allows the low-dimensional subspace from which each image/signal is generated to change with time in a piecewise constant fashion.
Subspace Tracking from Missing and Outlier Corrupted Data
Oct 06, 2018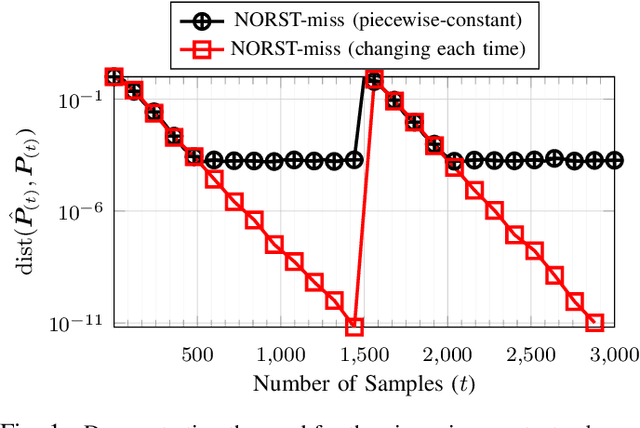
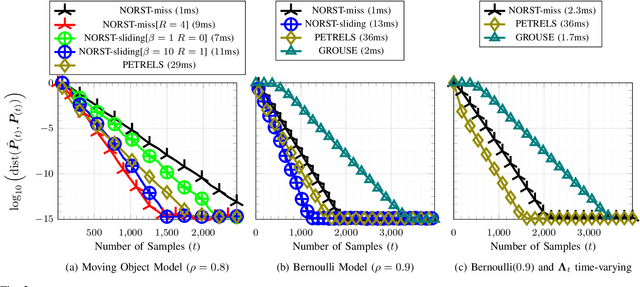


Abstract:We study the related problems of subspace tracking in the presence of missing data (ST-miss) as well as robust subspace tracking with missing data (RST-miss). Here "robust" refers to robustness to sparse outliers. In recent work, we have studied the RST problem without missing data. In this work, we show that simple modifications of our solution approach for RST also provably solve ST-miss and RST-miss under weaker and similar assumptions respectively. To our knowledge, our result is the first complete guarantee for both ST-miss and RST-miss. This means we are able to show that, under assumptions on only the algorithm inputs (input data and/or initialization), the output subspace estimates are close to the true data subspaces at all times. Our guarantees hold under mild and easily interpretable assumptions and handle time-varying subspaces (unlike all previous work). We also show that our algorithm and its extensions are fast and have competitive experimental performance when compared with existing methods.
Provable Dynamic Robust PCA or Robust Subspace Tracking
Sep 19, 2018


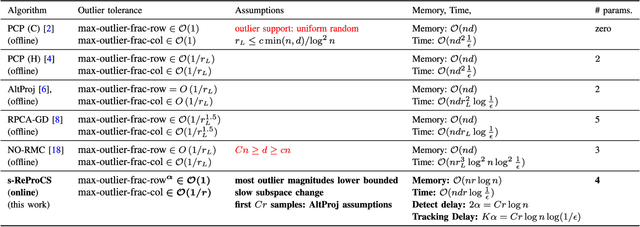
Abstract:Dynamic robust PCA refers to the dynamic (time-varying) extension of robust PCA (RPCA). It assumes that the true (uncorrupted) data lies in a low-dimensional subspace that can change with time, albeit slowly. The goal is to track this changing subspace over time in the presence of sparse outliers. We develop and study a novel algorithm, that we call simple-ReProCS, based on the recently introduced Recursive Projected Compressive Sensing (ReProCS) framework. Our work provides the first guarantee for dynamic RPCA that holds under weakened versions of standard RPCA assumptions, slow subspace change and a lower bound assumption on most outlier magnitudes. Our result is significant because (i) it removes the strong assumptions needed by the two previous complete guarantees for ReProCS-based algorithms; (ii) it shows that it is possible to achieve significantly improved outlier tolerance, compared with all existing RPCA or dynamic RPCA solutions by exploiting the above two simple extra assumptions; and (iii) it proves that simple-ReProCS is online (after initialization), fast, and, has near-optimal memory complexity.
Nearly Optimal Robust Subspace Tracking
Jul 06, 2018



Abstract:In this work, we study the robust subspace tracking (RST) problem and obtain one of the first two provable guarantees for it. The goal of RST is to track sequentially arriving data vectors that lie in a slowly changing low-dimensional subspace, while being robust to corruption by additive sparse outliers. It can also be interpreted as a dynamic (time-varying) extension of robust PCA (RPCA), with the minor difference that RST also requires a short tracking delay. We develop a recursive projected compressive sensing algorithm that we call Nearly Optimal RST via ReProCS (ReProCS-NORST) because its tracking delay is nearly optimal. We prove that NORST solves both the RST and the dynamic RPCA problems under weakened standard RPCA assumptions, two simple extra assumptions (slow subspace change and most outlier magnitudes lower bounded), and a few minor assumptions. Our guarantee shows that NORST enjoys a near optimal tracking delay of $O(r \log n \log(1/\epsilon))$. Its required delay between subspace change times is the same, and its memory complexity is $n$ times this value. Thus both these are also nearly optimal. Here $n$ is the ambient space dimension, $r$ is the subspaces' dimension, and $\epsilon$ is the tracking accuracy. NORST also has the best outlier tolerance compared with all previous RPCA or RST methods, both theoretically and empirically (including for real videos), without requiring any model on how the outlier support is generated. This is possible because of the extra assumptions it uses.
Robust Subspace Learning: Robust PCA, Robust Subspace Tracking, and Robust Subspace Recovery
Jul 05, 2018



Abstract:PCA is one of the most widely used dimension reduction techniques. A related easier problem is "subspace learning" or "subspace estimation". Given relatively clean data, both are easily solved via singular value decomposition (SVD). The problem of subspace learning or PCA in the presence of outliers is called robust subspace learning or robust PCA (RPCA). For long data sequences, if one tries to use a single lower dimensional subspace to represent the data, the required subspace dimension may end up being quite large. For such data, a better model is to assume that it lies in a low-dimensional subspace that can change over time, albeit gradually. The problem of tracking such data (and the subspaces) while being robust to outliers is called robust subspace tracking (RST). This article provides a magazine-style overview of the entire field of robust subspace learning and tracking. In particular solutions for three problems are discussed in detail: RPCA via sparse+low-rank matrix decomposition (S+LR), RST via S+LR, and "robust subspace recovery (RSR)". RSR assumes that an entire data vector is either an outlier or an inlier. The S+LR formulation instead assumes that outliers occur on only a few data vector indices and hence are well modeled as sparse corruptions.
* To appear, IEEE Signal Processing Magazine, July 2018
Static and Dynamic Robust PCA and Matrix Completion: A Review
May 25, 2018



Abstract:Principal Components Analysis (PCA) is one of the most widely used dimension reduction techniques. Robust PCA (RPCA) refers to the problem of PCA when the data may be corrupted by outliers. Recent work by Cand{\`e}s, Wright, Li, and Ma defined RPCA as a problem of decomposing a given data matrix into the sum of a low-rank matrix (true data) and a sparse matrix (outliers). The column space of the low-rank matrix then gives the PCA solution. This simple definition has lead to a large amount of interesting new work on provably correct, fast, and practical solutions to RPCA. More recently, the dynamic (time-varying) version of the RPCA problem has been studied and a series of provably correct, fast, and memory efficient tracking solutions have been proposed. Dynamic RPCA (or robust subspace tracking) is the problem of tracking data lying in a (slowly) changing subspace while being robust to sparse outliers. This article provides an exhaustive review of the last decade of literature on RPCA and its dynamic counterpart (robust subspace tracking), along with describing their theoretical guarantees, discussing the pros and cons of various approaches, and providing empirical comparisons of performance and speed. A brief overview of the (low-rank) matrix completion literature is also provided (the focus is on works not discussed in other recent reviews). This refers to the problem of completing a low-rank matrix when only a subset of its entries are observed. It can be interpreted as a simpler special case of RPCA in which the indices of the outlier corrupted entries are known.
* To appear in Proceedings of the IEEE, Special Issue on Rethinking PCA for Modern Datasets. arXiv admin note: text overlap with arXiv:1711.09492
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge