Phaseless Low Rank Matrix Recovery and Subspace Tracking

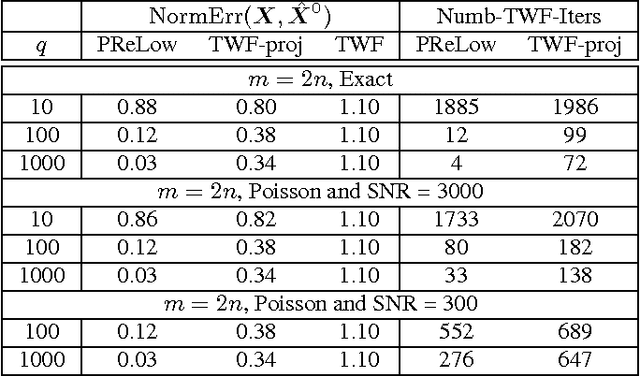
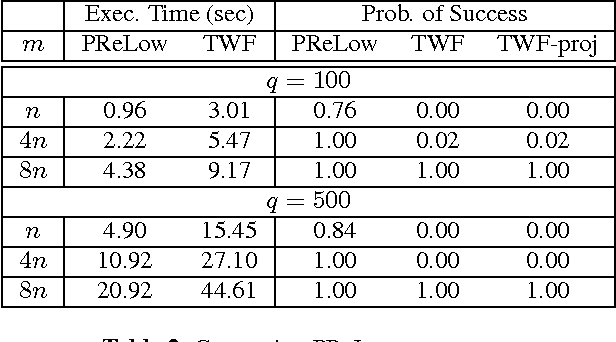
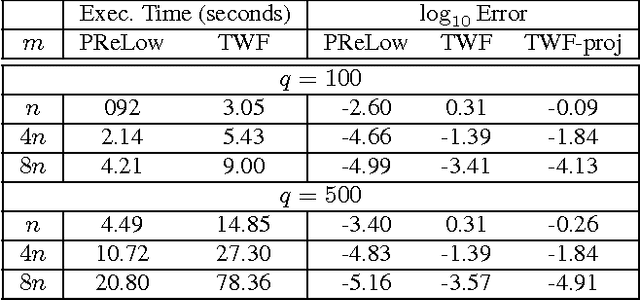
This work introduces the first simple and provably correct solution for recovering a low-rank matrix from phaseless (magnitude-only) linear projections of each of its columns. This problem finds important applications in phaseless dynamic imaging, e.g., Fourier ptychographic imaging of live biological specimens. We demonstrate the practical advantage of our proposed approach, AltMinLowRaP, over existing work via extensive simulation, and some real-data, experiments. Under a right incoherence (denseness of right singular vectors) assumption, our guarantee shows that, in the regime of small ranks, r, the sample complexity of AltMinLowRaP is much smaller than what standard phase retrieval methods need; and it is only $r^3$ times the order-optimal complexity for low-rank matrix recovery. We also provide a solution for a dynamic extension of the above problem. This allows the low-dimensional subspace from which each image/signal is generated to change with time in a piecewise constant fashion.