Matrix Approximation with Side Information: When Column Sampling is Enough

A novel matrix approximation problem is considered herein: observations based on a few fully sampled columns and quasi-polynomial structural side information are exploited. The framework is motivated by quantum chemistry problems wherein full matrix computation is expensive, and partial computations only lead to column information. The proposed algorithm successfully estimates the column and row-space of a true matrix given a priori structural knowledge of the true matrix. A theoretical spectral error bound is provided, which captures the possible inaccuracies of the side information. The error bound proves it scales in its signal-to-noise (SNR) ratio. The proposed algorithm is validated via simulations which enable the characterization of the amount of information provided by the quasi-polynomial side information.

Distributed Online Learning with Multiple Kernels

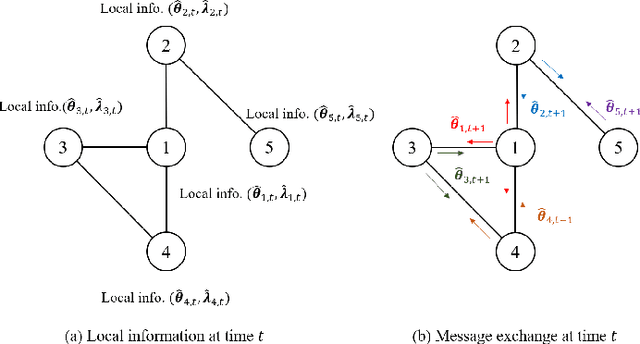
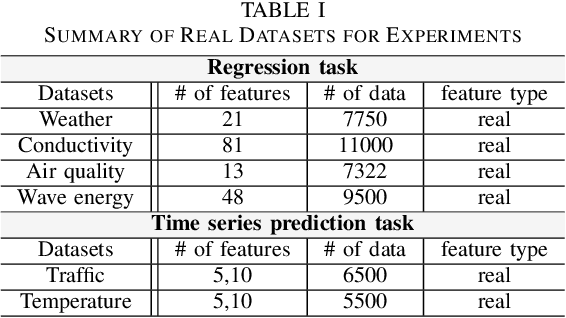
We consider the problem of learning a nonlinear function over a network of learners in a fully decentralized fashion. Online learning is additionally assumed, where every learner receives continuous streaming data locally. This learning model is called a fully distributed online learning (or a fully decentralized online federated learning). For this model, we propose a novel learning framework with multiple kernels, which is named DOMKL. The proposed DOMKL is devised by harnessing the principles of an online alternating direction method of multipliers and a distributed Hedge algorithm. We theoretically prove that DOMKL over T time slots can achieve an optimal sublinear regret, implying that every learner in the network can learn a common function which has a diminishing gap from the best function in hindsight. Our analysis also reveals that DOMKL yields the same asymptotic performance of the state-of-the-art centralized approach while keeping local data at edge learners. Via numerical tests with real datasets, we demonstrate the effectiveness of the proposed DOMKL on various online regression and time-series prediction tasks.

Multiple Kernel-Based Online Federated Learning

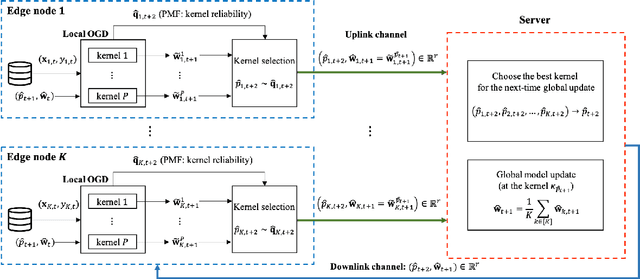
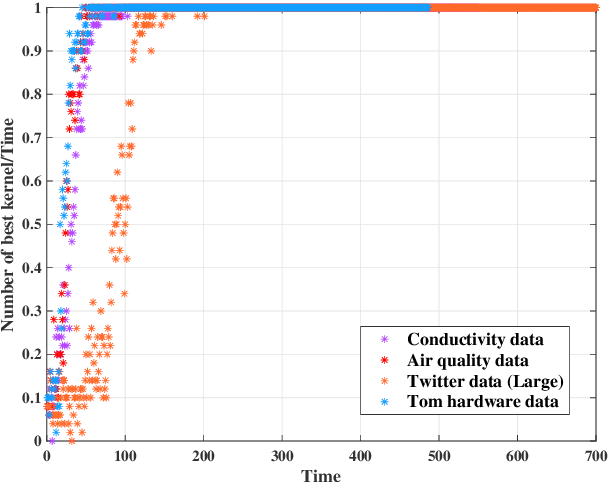
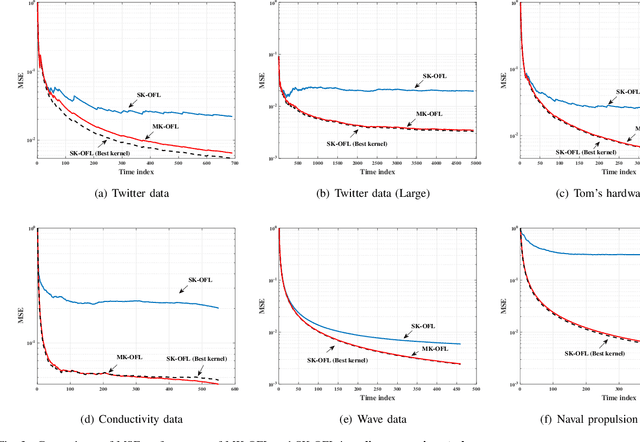
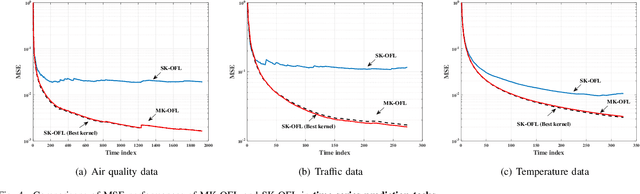
Online federated learning (OFL) becomes an emerging learning framework, in which edge nodes perform online learning with continuous streaming local data and a server constructs a global model from the aggregated local models. Online multiple kernel learning (OMKL), using a preselected set of P kernels, can be a good candidate for OFL framework as it has provided an outstanding performance with a low-complexity and scalability. Yet, an naive extension of OMKL into OFL framework suffers from a heavy communication overhead that grows linearly with P. In this paper, we propose a novel multiple kernel-based OFL (MK-OFL) as a non-trivial extension of OMKL, which yields the same performance of the naive extension with 1/P communication overhead reduction. We theoretically prove that MK-OFL achieves the optimal sublinear regret bound when compared with the best function in hindsight. Finally, we provide the numerical tests of our approach on real-world datasets, which suggests its practicality.

Pool-based sequential active learning with multi kernels

We study a pool-based sequential active learning (AL), in which one sample is queried at each time from a large pool of unlabeled data according to a selection criterion. For this framework, we propose two selection criteria, named expected-kernel-discrepancy (EKD) and expected-kernel-loss (EKL), by leveraging the particular structure of multiple kernel learning (MKL). Also, it is identified that the proposed EKD and EKL successfully generalize the concepts of popular query-by-committee (QBC) and expected-model-change (EMC), respectively. Via experimental results with real-data sets, we verify the effectiveness of the proposed criteria compared with the existing methods.

Active Learning with Multiple Kernels

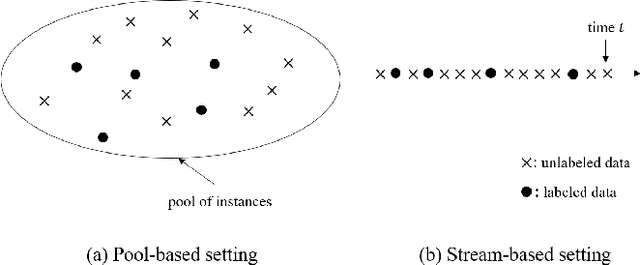
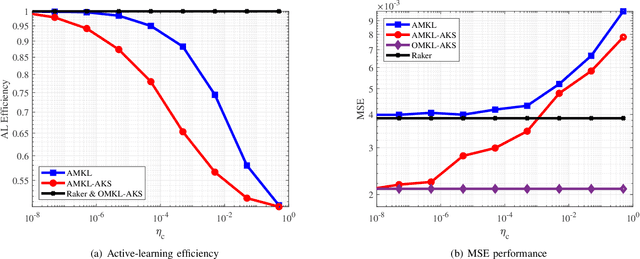
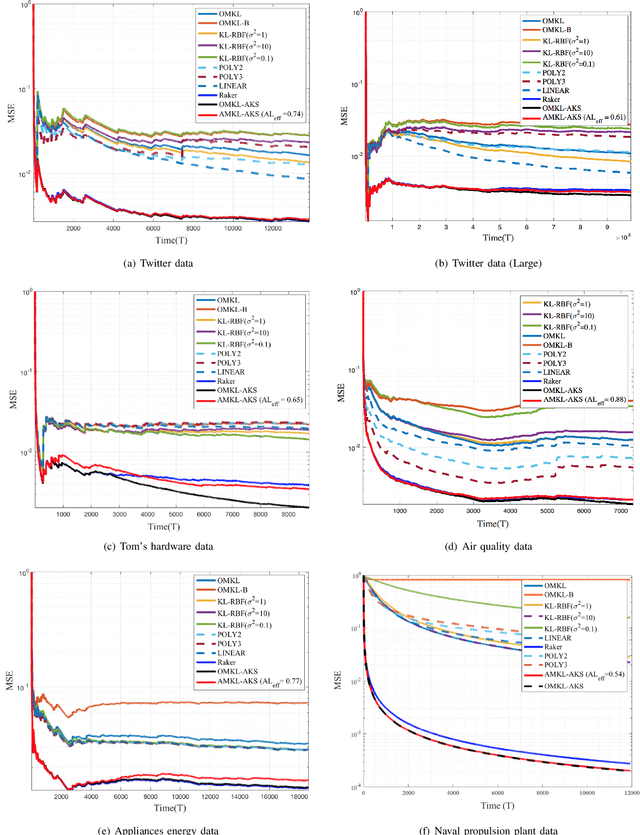
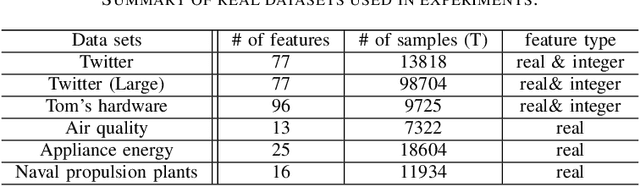
Online multiple kernel learning (OMKL) has provided an attractive performance in nonlinear function learning tasks. Leveraging a random feature approximation, the major drawback of OMKL, known as the curse of dimensionality, has been recently alleviated. In this paper, we introduce a new research problem, termed (stream-based) active multiple kernel learning (AMKL), in which a learner is allowed to label selected data from an oracle according to a selection criterion. This is necessary in many real-world applications as acquiring true labels is costly or time-consuming. We prove that AMKL achieves an optimal sublinear regret, implying that the proposed selection criterion indeed avoids unuseful label-requests. Furthermore, we propose AMKL with an adaptive kernel selection (AMKL-AKS) in which irrelevant kernels can be excluded from a kernel dictionary 'on the fly'. This approach can improve the efficiency of active learning as well as the accuracy of a function approximation. Via numerical tests with various real datasets, it is demonstrated that AMKL-AKS yields a similar or better performance than the best-known OMKL, with a smaller number of labeled data.