Distributed Online Learning with Multiple Kernels
Paper and Code
Feb 26, 2021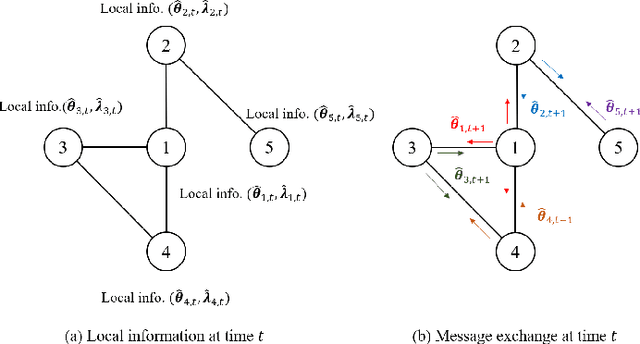
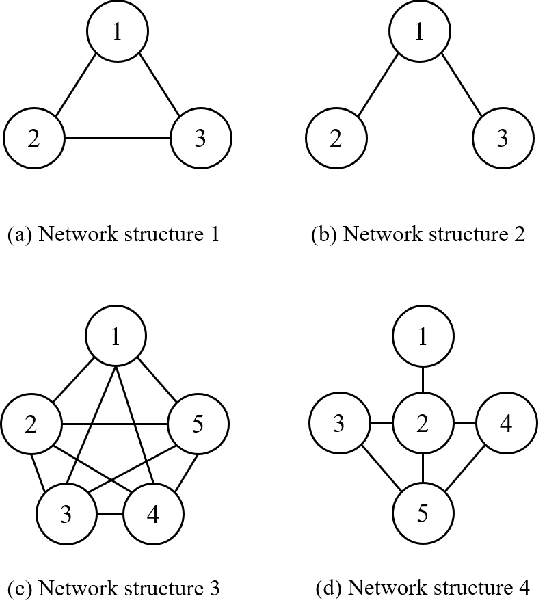
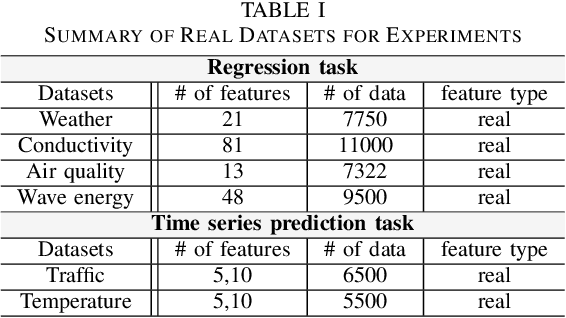

We consider the problem of learning a nonlinear function over a network of learners in a fully decentralized fashion. Online learning is additionally assumed, where every learner receives continuous streaming data locally. This learning model is called a fully distributed online learning (or a fully decentralized online federated learning). For this model, we propose a novel learning framework with multiple kernels, which is named DOMKL. The proposed DOMKL is devised by harnessing the principles of an online alternating direction method of multipliers and a distributed Hedge algorithm. We theoretically prove that DOMKL over T time slots can achieve an optimal sublinear regret, implying that every learner in the network can learn a common function which has a diminishing gap from the best function in hindsight. Our analysis also reveals that DOMKL yields the same asymptotic performance of the state-of-the-art centralized approach while keeping local data at edge learners. Via numerical tests with real datasets, we demonstrate the effectiveness of the proposed DOMKL on various online regression and time-series prediction tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge