Synthetic Data and Simulators for Recommendation Systems: Current State and Future Directions

Synthetic data and simulators have the potential to markedly improve the performance and robustness of recommendation systems. These approaches have already had a beneficial impact in other machine-learning driven fields. We identify and discuss a key trade-off between data fidelity and privacy in the past work on synthetic data and simulators for recommendation systems. For the important use case of predicting algorithm rankings on real data from synthetic data, we provide motivation and current successes versus limitations. Finally we outline a number of exciting future directions for recommendation systems that we believe deserve further attention and work, including mixing real and synthetic data, feedback in dataset generation, robust simulations, and privacy-preserving methods.

Unsupervised Distribution Learning for Lunar Surface Anomaly Detection

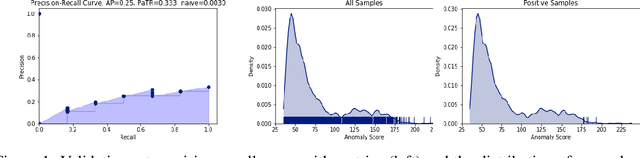
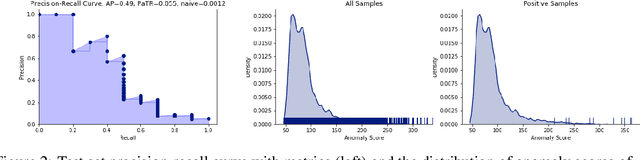
In this work we show that modern data-driven machine learning techniques can be successfully applied on lunar surface remote sensing data to learn, in an unsupervised way, sufficiently good representations of the data distribution to enable lunar technosignature and anomaly detection. In particular we train an unsupervised distribution learning neural network model to find the Apollo 15 landing module in a testing dataset, with no dataset specific model or hyperparameter tuning. Sufficiently good unsupervised data density estimation has the promise of enabling myriad useful downstream tasks, including locating lunar resources for future space flight and colonization, finding new impact craters or lunar surface reshaping, and algorithmically deciding the importance of unlabeled samples to send back from power- and bandwidth-constrained missions. We show in this work that such unsupervised learning can be successfully done in the lunar remote sensing and space science contexts.

Large-Scale Visual Active Learning with Deep Probabilistic Ensembles

Annotating the right data for training deep neural networks is an important challenge. Active learning using uncertainty estimates from Bayesian Neural Networks (BNNs) could provide an effective solution to this. Despite being theoretically principled, BNNs require approximations to be applied to large-scale problems, where both performance and uncertainty estimation are crucial. In this paper, we introduce Deep Probabilistic Ensembles (DPEs), a scalable technique that uses a regularized ensemble to approximate a deep BNN. We conduct a series of large-scale visual active learning experiments to evaluate DPEs on classification with the CIFAR-10, CIFAR-100 and ImageNet datasets, and semantic segmentation with the BDD100k dataset. Our models require significantly less training data to achieve competitive performances, and steadily improve upon strong active learning baselines as the annotation budget is increased.

Deep Probabilistic Ensembles: Approximate Variational Inference through KL Regularization

In this paper, we introduce Deep Probabilistic Ensembles (DPEs), a scalable technique that uses a regularized ensemble to approximate a deep Bayesian Neural Network (BNN). We do so by incorporating a KL divergence penalty term into the training objective of an ensemble, derived from the evidence lower bound used in variational inference. We evaluate the uncertainty estimates obtained from our models for active learning on visual classification. Our approach steadily improves upon active learning baselines as the annotation budget is increased.

The Relevance of Bayesian Layer Positioning to Model Uncertainty in Deep Bayesian Active Learning

One of the main challenges of deep learning tools is their inability to capture model uncertainty. While Bayesian deep learning can be used to tackle the problem, Bayesian neural networks often require more time and computational power to train than deterministic networks. Our work explores whether fully Bayesian networks are needed to successfully capture model uncertainty. We vary the number and position of Bayesian layers in a network and compare their performance on active learning with the MNIST dataset. We found that we can fully capture the model uncertainty by using only a few Bayesian layers near the output of the network, combining the advantages of deterministic and Bayesian networks.

How Much Did it Rain? Predicting Real Rainfall Totals Based on Radar Data

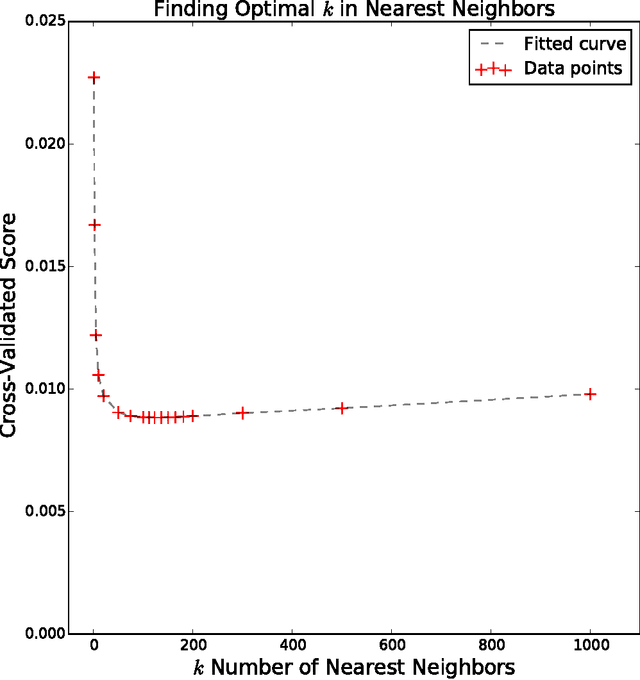
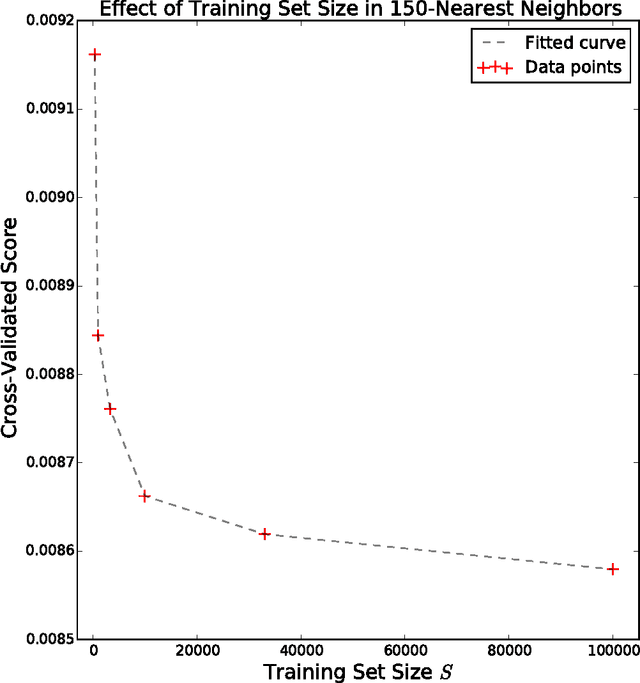
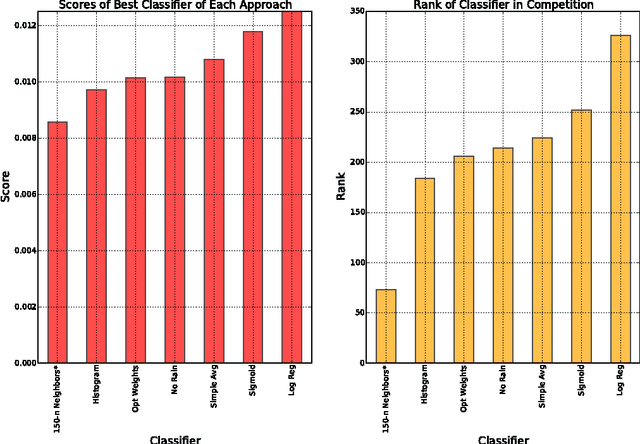
We applied a variety of parametric and non-parametric machine learning models to predict the probability distribution of rainfall based on 1M training examples over a single year across several U.S. states. Our top performing model based on a squared loss objective was a cross-validated parametric k-nearest-neighbor predictor that took about six days to compute, and was competitive in a world-wide competition.