UQ of 2D Slab Burner DNS: Surrogates, Uncertainty Propagation, and Parameter Calibration

The goal of this paper is to demonstrate and address challenges related to all aspects of performing a complete uncertainty quantification (UQ) analysis of a complicated physics-based simulation like a 2D slab burner direct numerical simulation (DNS). The UQ framework includes the development of data-driven surrogate models, propagation of parametric uncertainties to the fuel regression rate--the primary quantity of interest--and Bayesian calibration of critical parameters influencing the regression rate using experimental data. Specifically, the parameters calibrated include the latent heat of sublimation and a chemical reaction temperature exponent. Two surrogate models, a Gaussian Process (GP) and a Hierarchical Multiscale Surrogate (HMS) were constructed using an ensemble of 64 simulations generated via Latin Hypercube sampling. Both models exhibited comparable performance during cross-validation. However, the HMS was more stable due to its ability to handle multiscale effects, in contrast with the GP which was very sensitive to kernel choice. Analysis revealed that the surrogates do not accurately predict all spatial locations of the slab burner as-is. Subsequent Bayesian calibration of the physical parameters against experimental observations resulted in regression rate predictions that closer align with experimental observation in specific regions. This study highlights the importance of surrogate model selection and parameter calibration in quantifying uncertainty in predictions of fuel regression rates in complex combustion systems.

Large Deviations for Accelerating Neural Networks Training

Artificial neural networks (ANNs) require tremendous amount of data to train on. However, in classification models, most data features are often similar which can lead to increase in training time without significant improvement in the performance. Thus, we hypothesize that there could be a more efficient way to train an ANN using a better representative sample. For this, we propose the LAD Improved Iterative Training (LIIT), a novel training approach for ANN using large deviations principle to generate and iteratively update training samples in a fast and efficient setting. This is exploratory work with extensive opportunities for future work. The thesis presents this ongoing research work with the following contributions from this study: (1) We propose a novel ANN training method, LIIT, based on the large deviations theory where additional dimensionality reduction is not needed to study high dimensional data. (2) The LIIT approach uses a Modified Training Sample (MTS) that is generated and iteratively updated using a LAD anomaly score based sampling strategy. (3) The MTS sample is designed to be well representative of the training data by including most anomalous of the observations in each class. This ensures distinct patterns and features are learnt with smaller samples. (4) We study the classification performance of the LIIT trained ANNs with traditional batch trained counterparts.

An Ensemble-Based Deep Framework for Estimating Thermo-Chemical State Variables from Flamelet Generated Manifolds

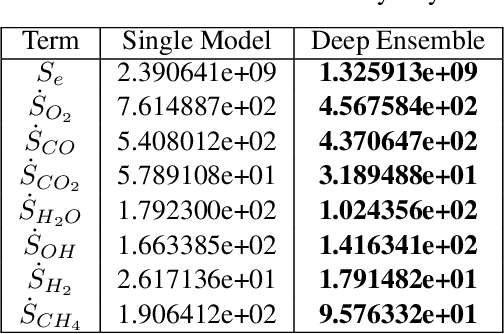
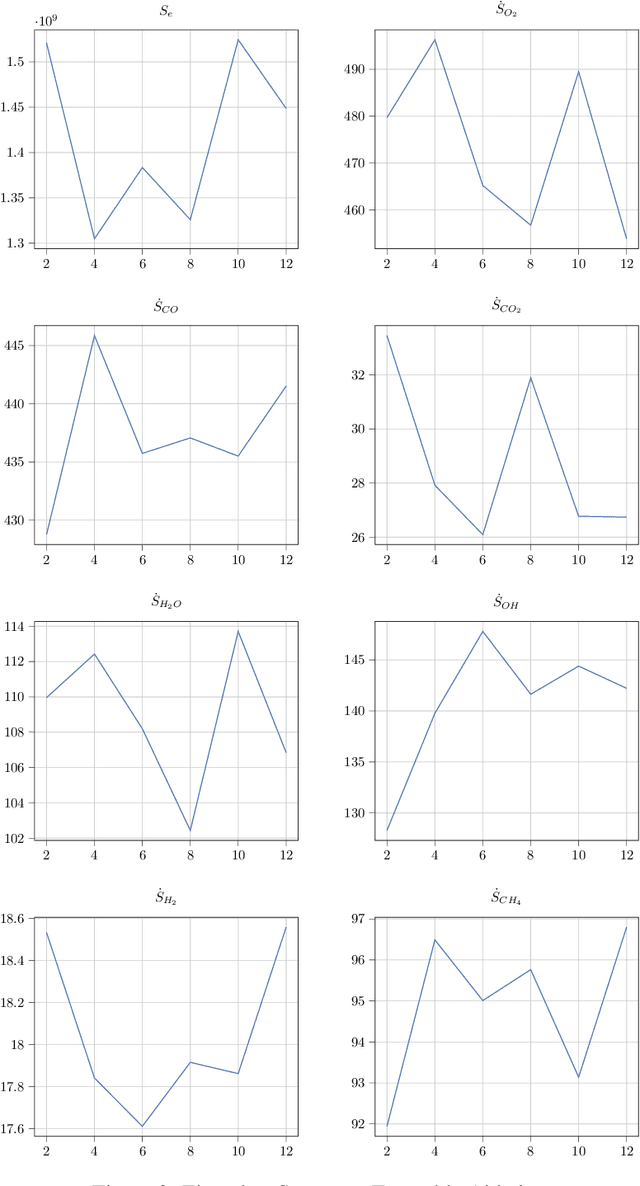
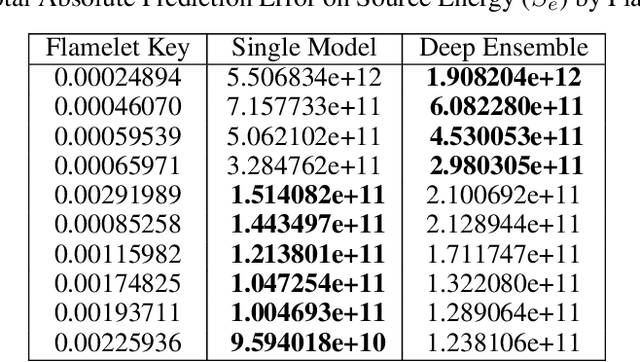
Complete computation of turbulent combustion flow involves two separate steps: mapping reaction kinetics to low-dimensional manifolds and looking-up this approximate manifold during CFD run-time to estimate the thermo-chemical state variables. In our previous work, we showed that using a deep architecture to learn the two steps jointly, instead of separately, is 73% more accurate at estimating the source energy, a key state variable, compared to benchmarks and can be integrated within a DNS turbulent combustion framework. In their natural form, such deep architectures do not allow for uncertainty quantification of the quantities of interest: the source energy and key species source terms. In this paper, we expand on such architectures, specifically ChemTab, by introducing deep ensembles to approximate the posterior distribution of the quantities of interest. We investigate two strategies of creating these ensemble models: one that keeps the flamelet origin information (Flamelets strategy) and one that ignores the origin and considers all the data independently (Points strategy). To train these models we used flamelet data generated by the GRI--Mech 3.0 methane mechanism, which consists of 53 chemical species and 325 reactions. Our results demonstrate that the Flamelets strategy is superior in terms of the absolute prediction error for the quantities of interest, but is reliant on the types of flamelets used to train the ensemble. The Points strategy is best at capturing the variability of the quantities of interest, independent of the flamelet types. We conclude that, overall, ChemTab Deep Ensembles allows for a more accurate representation of the source energy and key species source terms, compared to the model without these modifications.

Combined Data and Deep Learning Model Uncertainties: An Application to the Measurement of Solid Fuel Regression Rate

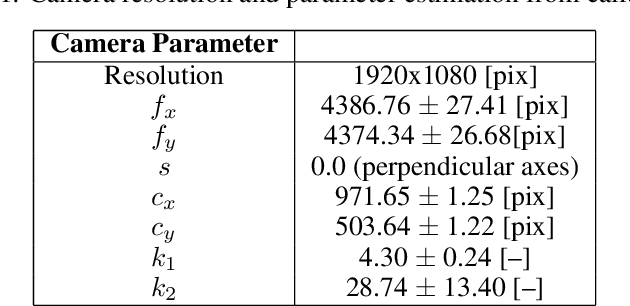
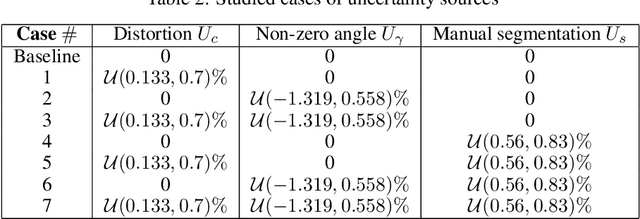
In complex physical process characterization, such as the measurement of the regression rate for solid hybrid rocket fuels, where both the observation data and the model used have uncertainties originating from multiple sources, combining these in a systematic way for quantities of interest(QoI) remains a challenge. In this paper, we present a forward propagation uncertainty quantification (UQ) process to produce a probabilistic distribution for the observed regression rate $\dot{r}$. We characterized two input data uncertainty sources from the experiment (the distortion from the camera $U_c$ and the non-zero angle fuel placement $U_\gamma$), the prediction and model form uncertainty from the deep neural network ($U_m$), as well as the variability from the manually segmented images used for training it ($U_s$). We conducted seven case studies on combinations of these uncertainty sources with the model form uncertainty. The main contribution of this paper is the investigation and inclusion of the experimental image data uncertainties involved, and how to include them in a workflow when the QoI is the result of multiple sequential processes.

Anomaly Detection for High-Dimensional Data Using Large Deviations Principle

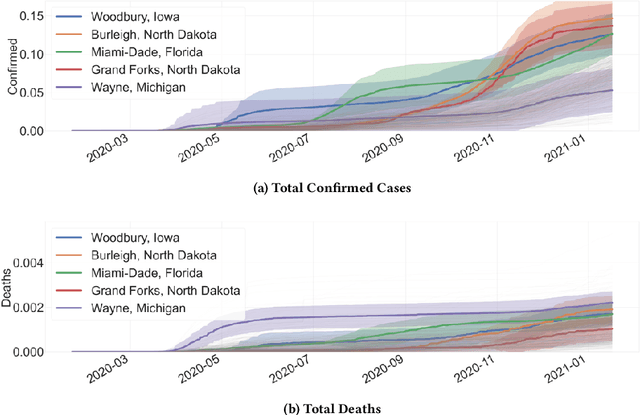
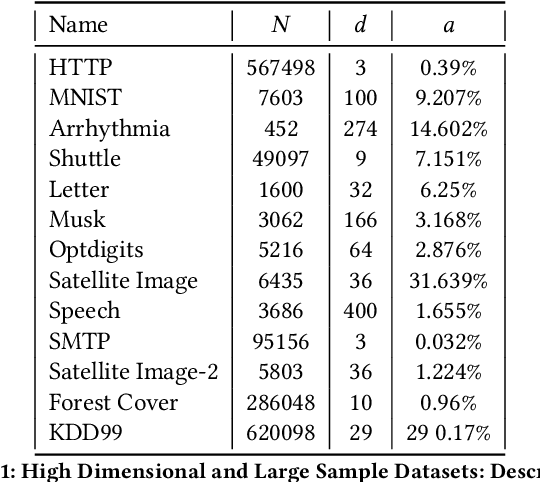
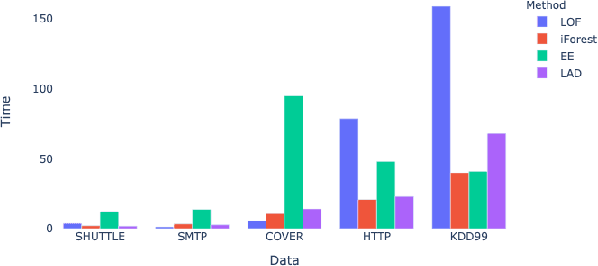
Most current anomaly detection methods suffer from the curse of dimensionality when dealing with high-dimensional data. We propose an anomaly detection algorithm that can scale to high-dimensional data using concepts from the theory of large deviations. The proposed Large Deviations Anomaly Detection (LAD) algorithm is shown to outperform state of art anomaly detection methods on a variety of large and high-dimensional benchmark data sets. Exploiting the ability of the algorithm to scale to high-dimensional data, we propose an online anomaly detection method to identify anomalies in a collection of multivariate time series. We demonstrate the applicability of the online algorithm in identifying counties in the United States with anomalous trends in terms of COVID-19 related cases and deaths. Several of the identified anomalous counties correlate with counties with documented poor response to the COVID pandemic.

Measurement of Hybrid Rocket Solid Fuel Regression Rate for a Slab Burner using Deep Learning

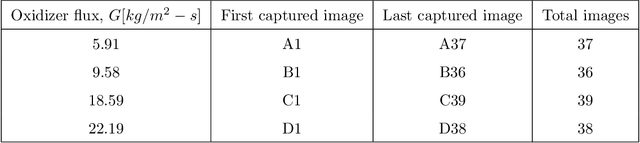
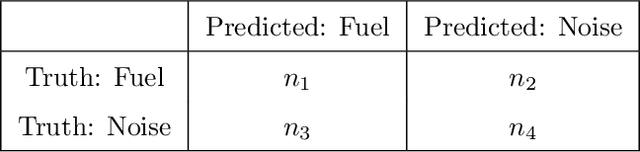
This study presents an imaging-based deep learning tool to measure the fuel regression rate in a 2D slab burner experiment for hybrid rocket fuels. The slab burner experiment is designed to verify mechanistic models of reacting boundary layer combustion in hybrid rockets by the measurement of fuel regression rates. A DSLR camera with a high intensity flash is used to capture images throughout the burn and the images are then used to find the fuel boundary to calculate the regression rate. A U-net convolutional neural network architecture is explored to segment the fuel from the experimental images. A Monte-Carlo Dropout process is used to quantify the regression rate uncertainty produced from the network. The U-net computed regression rates are compared with values from other techniques from literature and show error less than 10%. An oxidizer flux dependency study is performed and shows the U-net predictions of regression rates are accurate and independent of the oxidizer flux, when the images in the training set are not over-saturated. Training with monochrome images is explored and is not successful at predicting the fuel regression rate from images with high noise. The network is superior at filtering out noise introduced by soot, pitting, and wax deposition on the chamber glass as well as the flame when compared to traditional image processing techniques, such as threshold binary conversion and spatial filtering. U-net consistently provides low error image segmentations to allow accurate computation of the regression rate of the fuel.

A Forward Backward Greedy approach for Sparse Multiscale Learning

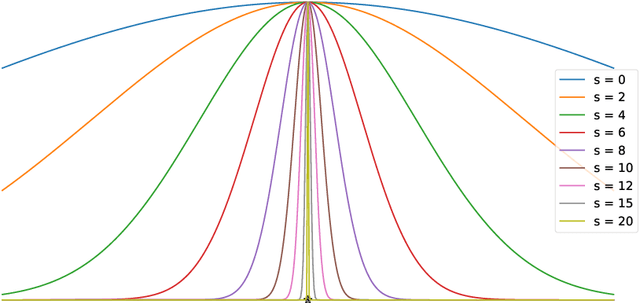
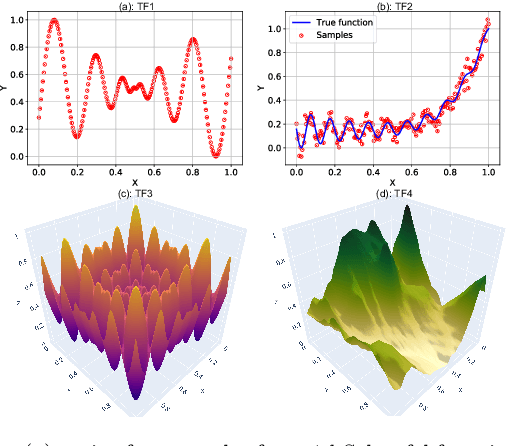
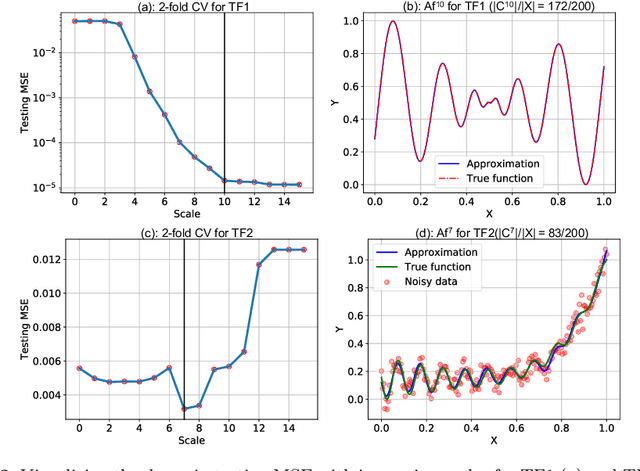
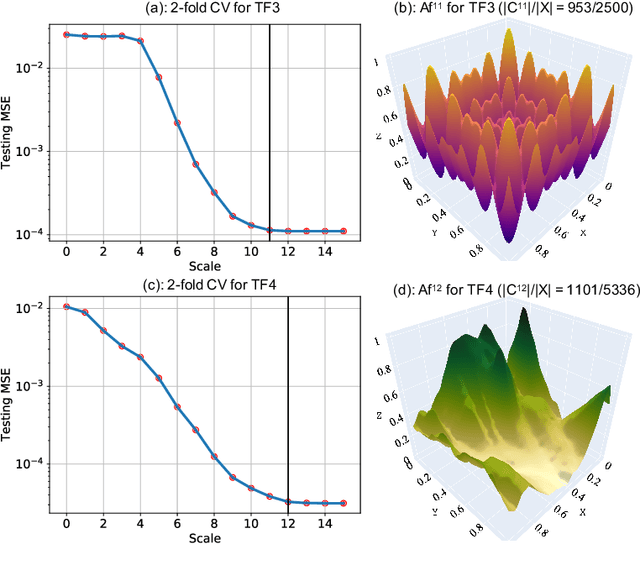
Multiscale Models are known to be successful in uncovering and analyzing the structures in data at different resolutions. In the current work we propose a feature driven Reproducing Kernel Hilbert space (RKHS), for which the associated kernel has a weighted multiscale structure. For generating approximations in this space, we provide a practical forward-backward algorithm that is shown to greedily construct a set of basis functions having a multiscale structure, while also creating sparse representations from the given data set, making representations and predictions very efficient. We provide a detailed analysis of the algorithm including recommendations for selecting algorithmic hyper-parameters and estimating probabilistic rates of convergence at individual scales. Then we extend this analysis to multiscale setting, studying the effects of finite scale truncation and quality of solution in the inherent RKHS. In the last section, we analyze the performance of the approach on a variety of simulation and real data sets, thereby justifying the efficiency claims in terms of model quality and data reduction.

Hierarchical regularization networks for sparsification based learning on noisy datasets

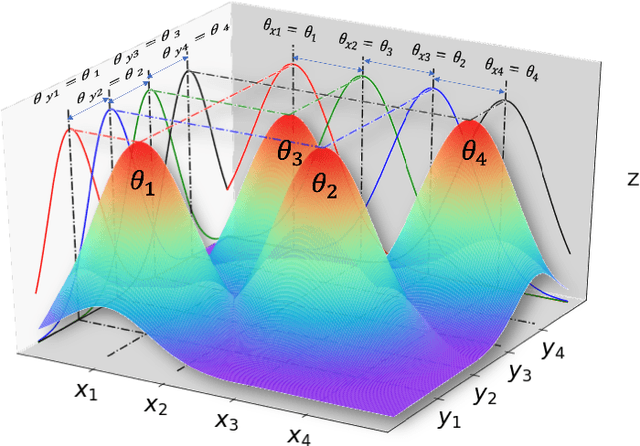
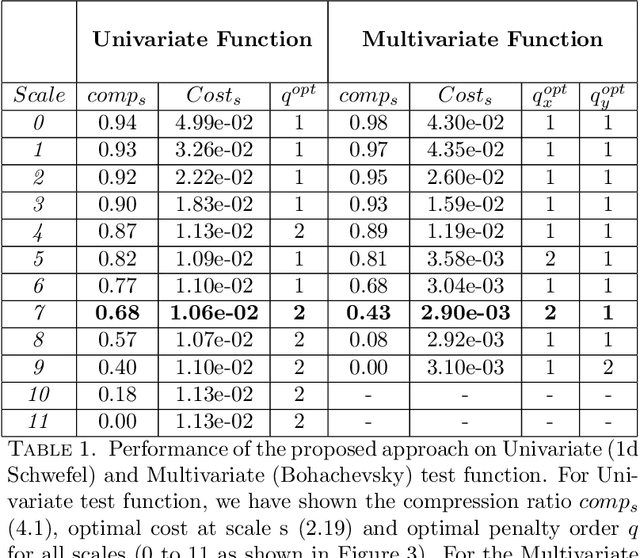
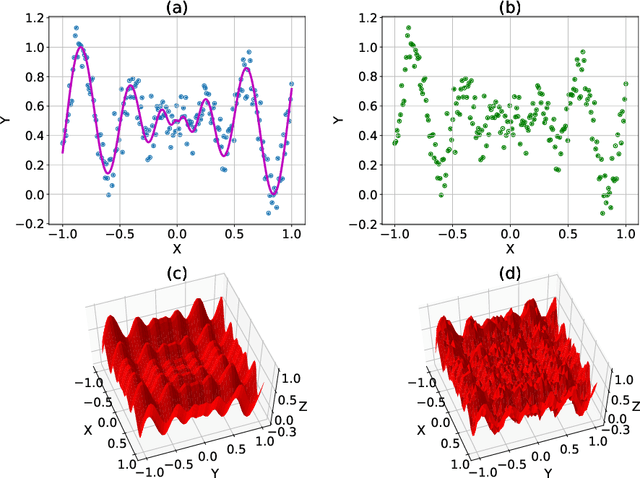
We propose a hierarchical learning strategy aimed at generating sparse representations and associated models for large noisy datasets. The hierarchy follows from approximation spaces identified at successively finer scales. For promoting model generalization at each scale, we also introduce a novel, projection based penalty operator across multiple dimension, using permutation operators for incorporating proximity and ordering information. The paper presents a detailed analysis of approximation properties in the reconstruction Reproducing Kernel Hilbert Spaces (RKHS) with emphasis on optimality and consistency of predictions and behavior of error functionals associated with the produced sparse representations. Results show the performance of the approach as a data reduction and modeling strategy on both synthetic (univariate and multivariate) and real datasets (time series). The sparse model for the test datasets, generated by the presented approach, is also shown to efficiently reconstruct the underlying process and preserve generalizability.

Hierarchical Data Reduction and Learning

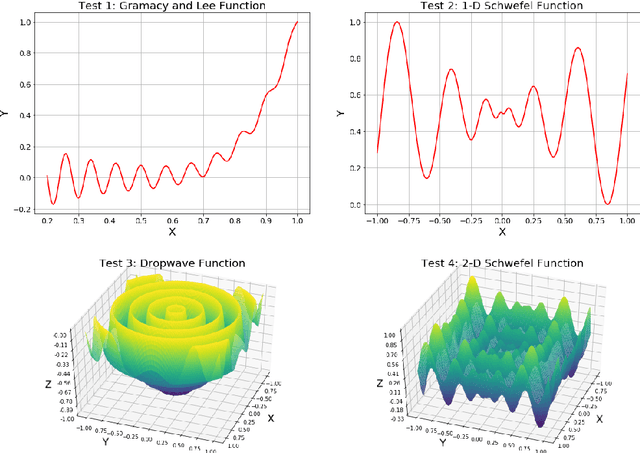
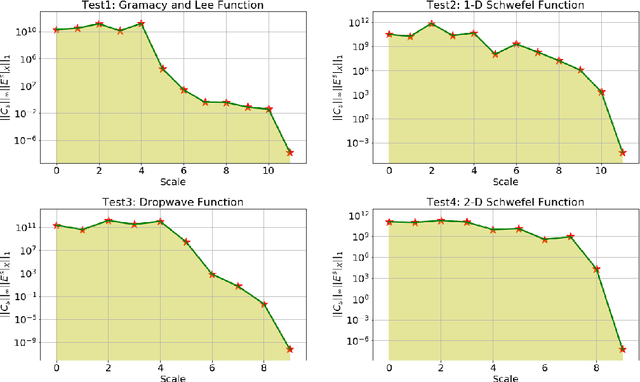
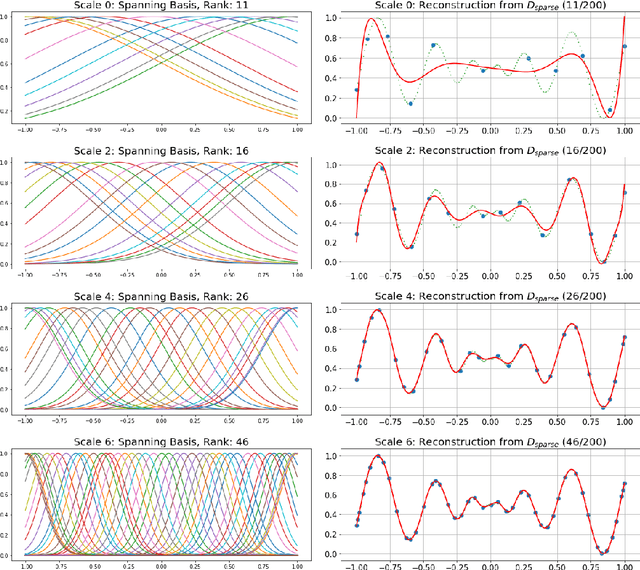
Paper proposes a hierarchical learning strategy for generation of sparse representations which capture the information content in large datasets and act as a model. The hierarchy arises from the approximation spaces considered at successively finer data dependent scales. Paper presents a detailed analysis of stability, convergence and behavior of error functionals associated with the approximations and well chosen set of applications. Results show the performance of the approach as a data reduction mechanism on both synthetic (univariate and multivariate) and real datasets (geo-spatial, computer vision and numerical model outcomes). The sparse model generated is shown to efficiently reconstruct data and minimize error in prediction.

Bayesian Anomaly Detection Using Extreme Value Theory

Data-driven anomaly detection methods typically build a model for the normal behavior of the target system, and score each data instance with respect to this model. A threshold is invariably needed to identify data instances with high (or low) scores as anomalies. This presents a practical limitation on the applicability of such methods, since most methods are sensitive to the choice of the threshold, and it is challenging to set optimal thresholds. We present a probabilistic framework to explicitly model the normal and anomalous behaviors and probabilistically reason about the data. An extreme value theory based formulation is proposed to model the anomalous behavior as the extremes of the normal behavior. As a specific instantiation, a joint non-parametric clustering and anomaly detection algorithm (INCAD) is proposed that models the normal behavior as a Dirichlet Process Mixture Model. A pseudo-Gibbs sampling based strategy is used for inference. Results on a variety of data sets show that the proposed method provides effective clustering and anomaly detection without requiring strong initialization and thresholding parameters.