Cross-Model Transferability of Adversarial Patches in Real-time Segmentation for Autonomous Driving

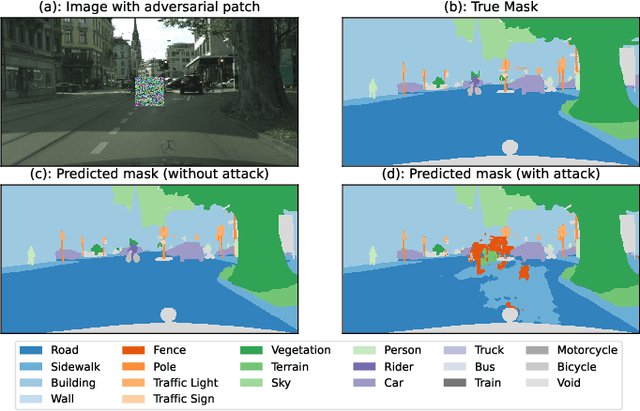
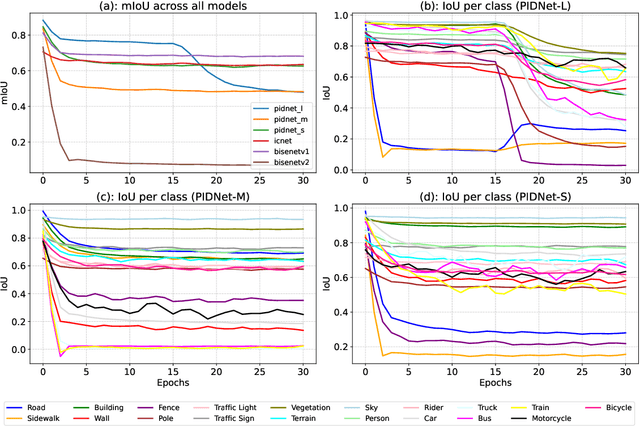
Adversarial attacks pose a significant threat to deep learning models, particularly in safety-critical applications like healthcare and autonomous driving. Recently, patch based attacks have demonstrated effectiveness in real-time inference scenarios owing to their 'drag and drop' nature. Following this idea for Semantic Segmentation (SS), here we propose a novel Expectation Over Transformation (EOT) based adversarial patch attack that is more realistic for autonomous vehicles. To effectively train this attack we also propose a 'simplified' loss function that is easy to analyze and implement. Using this attack as our basis, we investigate whether adversarial patches once optimized on a specific SS model, can fool other models or architectures. We conduct a comprehensive cross-model transferability analysis of adversarial patches trained on SOTA Convolutional Neural Network (CNN) models such PIDNet-S, PIDNet-M and PIDNet-L, among others. Additionally, we also include the Segformer model to study transferability to Vision Transformers (ViTs). All of our analysis is conducted on the widely used Cityscapes dataset. Our study reveals key insights into how model architectures (CNN vs CNN or CNN vs. Transformer-based) influence attack susceptibility. In particular, we conclude that although the transferability (effectiveness) of attacks on unseen images of any dimension is really high, the attacks trained against one particular model are minimally effective on other models. And this was found to be true for both ViT and CNN based models. Additionally our results also indicate that for CNN-based models, the repercussions of patch attacks are local, unlike ViTs. Per-class analysis reveals that simple-classes like 'sky' suffer less misclassification than others. The code for the project is available at: https://github.com/p-shekhar/adversarial-patch-transferability

Machine learning based surrogate modeling with SVD enabled training for nonlinear civil structures subject to dynamic loading

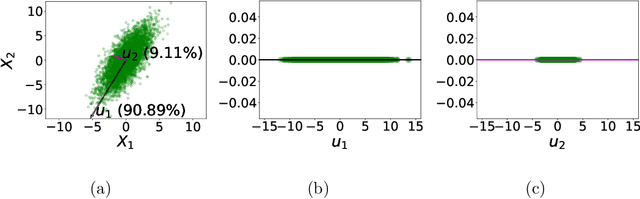
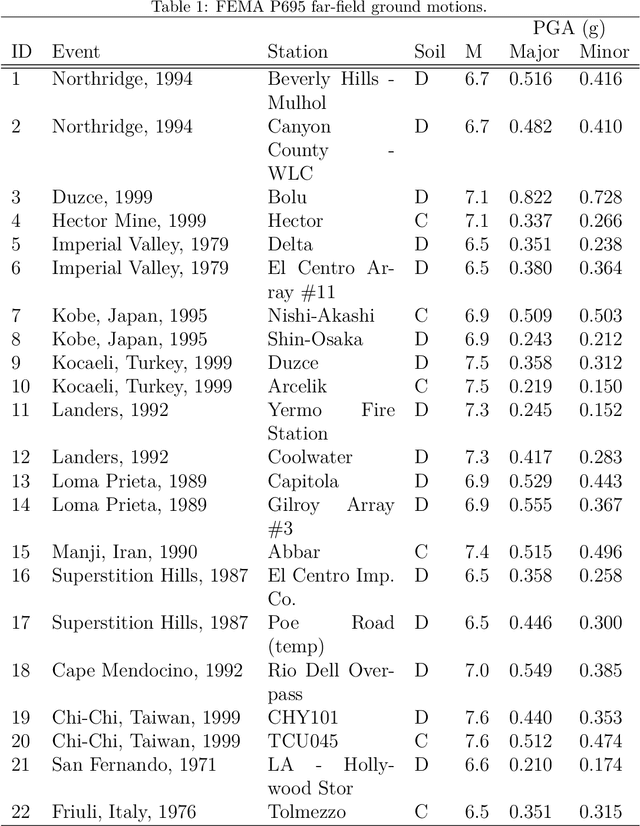
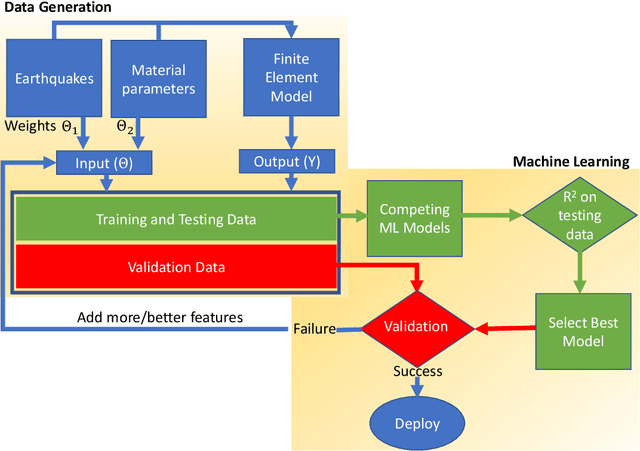
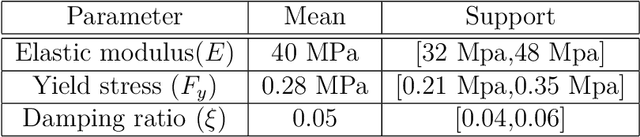
The computationally expensive estimation of engineering demand parameters (EDPs) via finite element (FE) models, while considering earthquake and parameter uncertainty limits the use of the Performance Based Earthquake Engineering framework. Attempts have been made to substitute FE models with surrogate models, however, most of these models are a function of building parameters only. This necessitates re-training for earthquakes not previously seen by the surrogate. In this paper, the authors propose a machine learning based surrogate model framework, which considers both these uncertainties in order to predict for unseen earthquakes. Accordingly,earthquakes are characterized by their projections on an orthonormal basis, computed using SVD of a representative ground motion suite. This enables one to generate large varieties of earthquakes by randomly sampling these weights and multiplying them with the basis. The weights along with the constitutive parameters serve as inputs to a machine learning model with EDPs as the desired output. Four competing machine learning models were tested and it was observed that a deep neural network (DNN) gave the most accurate prediction. The framework is validated by using it to successfully predict the peak response of one-story and three-story buildings represented using stick models, subjected to unseen far-field ground motions.

A Forward Backward Greedy approach for Sparse Multiscale Learning

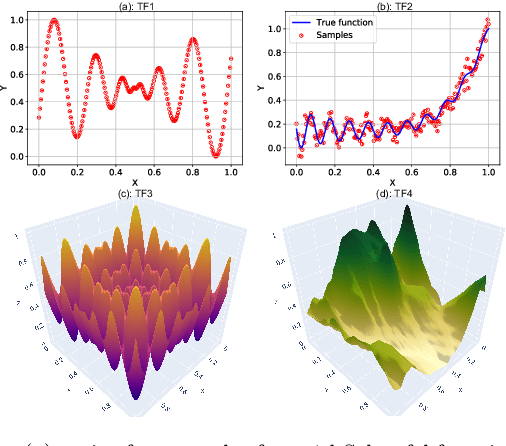
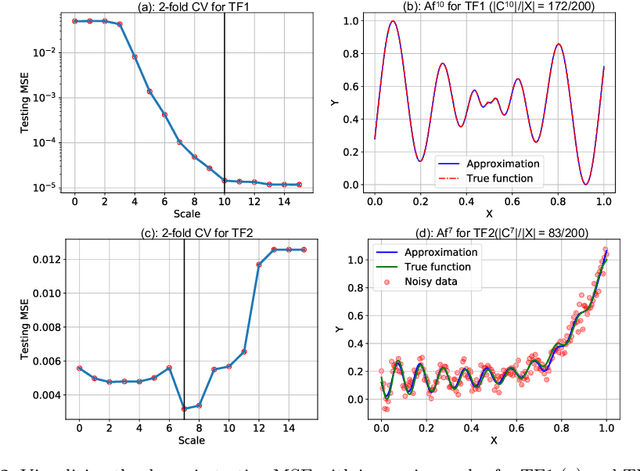
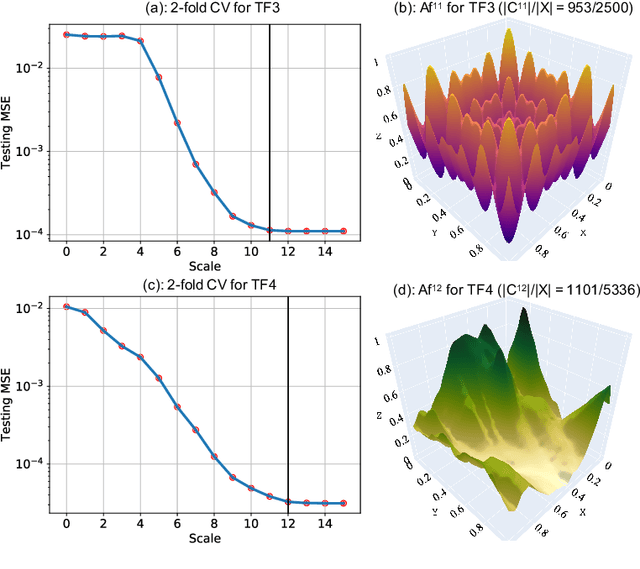
Multiscale Models are known to be successful in uncovering and analyzing the structures in data at different resolutions. In the current work we propose a feature driven Reproducing Kernel Hilbert space (RKHS), for which the associated kernel has a weighted multiscale structure. For generating approximations in this space, we provide a practical forward-backward algorithm that is shown to greedily construct a set of basis functions having a multiscale structure, while also creating sparse representations from the given data set, making representations and predictions very efficient. We provide a detailed analysis of the algorithm including recommendations for selecting algorithmic hyper-parameters and estimating probabilistic rates of convergence at individual scales. Then we extend this analysis to multiscale setting, studying the effects of finite scale truncation and quality of solution in the inherent RKHS. In the last section, we analyze the performance of the approach on a variety of simulation and real data sets, thereby justifying the efficiency claims in terms of model quality and data reduction.

Hierarchical regularization networks for sparsification based learning on noisy datasets

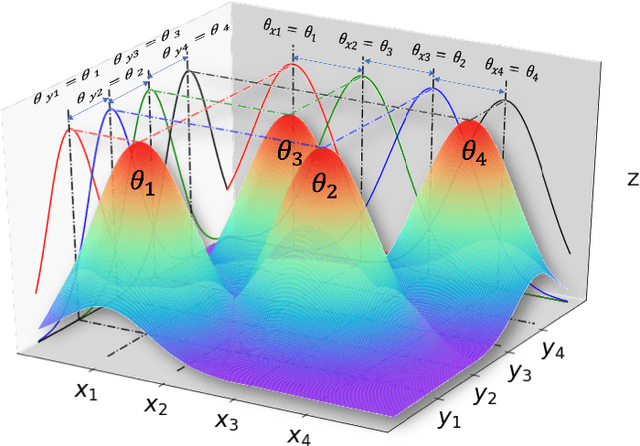
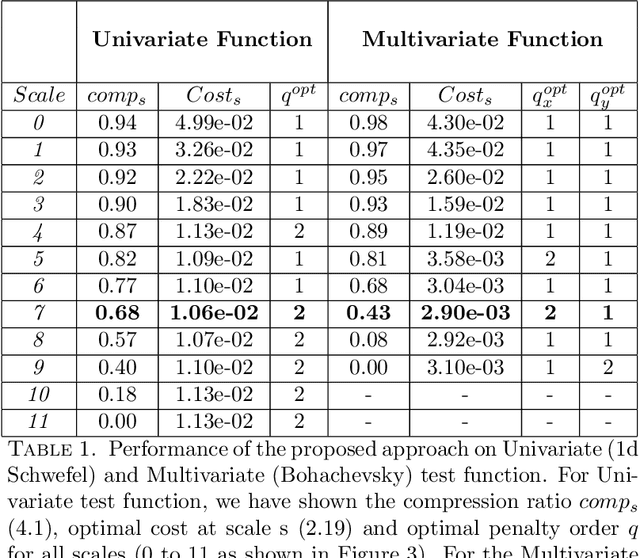
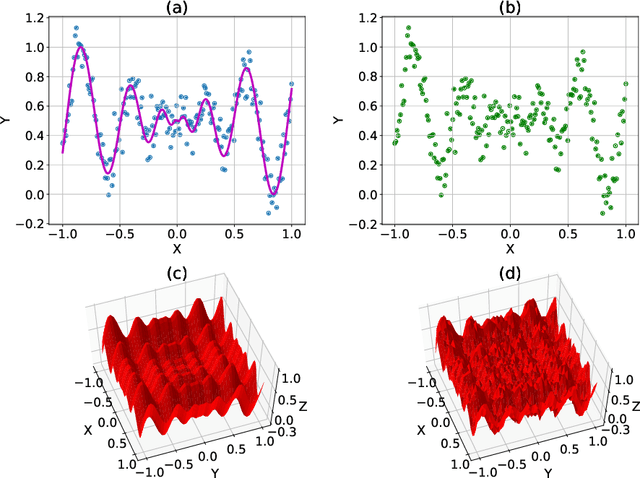
We propose a hierarchical learning strategy aimed at generating sparse representations and associated models for large noisy datasets. The hierarchy follows from approximation spaces identified at successively finer scales. For promoting model generalization at each scale, we also introduce a novel, projection based penalty operator across multiple dimension, using permutation operators for incorporating proximity and ordering information. The paper presents a detailed analysis of approximation properties in the reconstruction Reproducing Kernel Hilbert Spaces (RKHS) with emphasis on optimality and consistency of predictions and behavior of error functionals associated with the produced sparse representations. Results show the performance of the approach as a data reduction and modeling strategy on both synthetic (univariate and multivariate) and real datasets (time series). The sparse model for the test datasets, generated by the presented approach, is also shown to efficiently reconstruct the underlying process and preserve generalizability.

Hierarchical Data Reduction and Learning

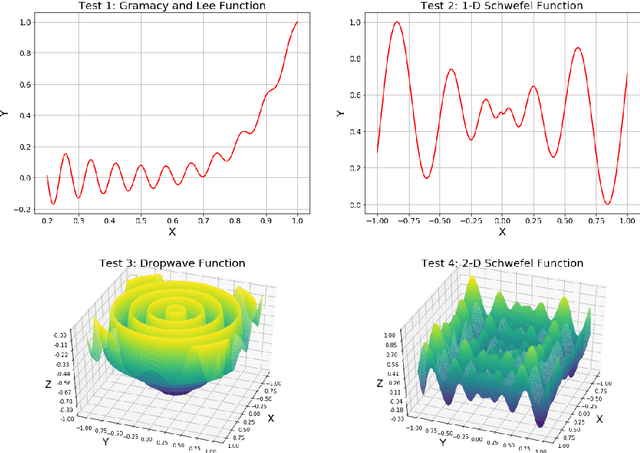
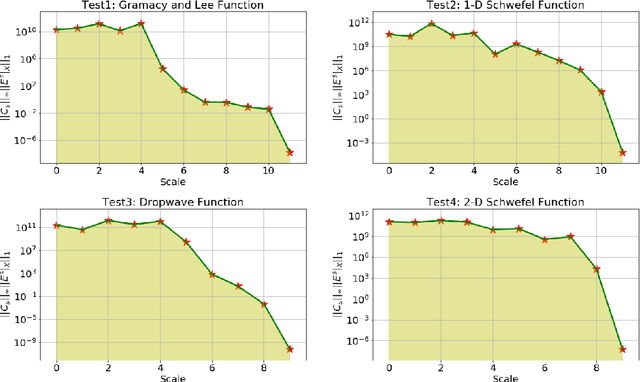
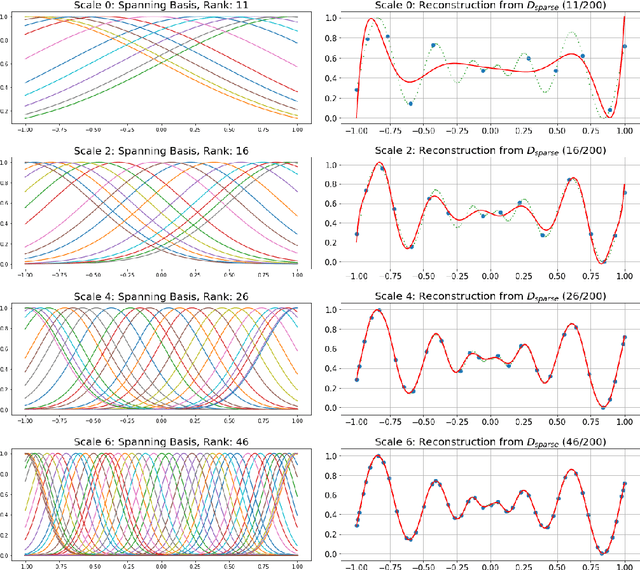
Paper proposes a hierarchical learning strategy for generation of sparse representations which capture the information content in large datasets and act as a model. The hierarchy arises from the approximation spaces considered at successively finer data dependent scales. Paper presents a detailed analysis of stability, convergence and behavior of error functionals associated with the approximations and well chosen set of applications. Results show the performance of the approach as a data reduction mechanism on both synthetic (univariate and multivariate) and real datasets (geo-spatial, computer vision and numerical model outcomes). The sparse model generated is shown to efficiently reconstruct data and minimize error in prediction.