Hierarchical Data Reduction and Learning
Paper and Code
Jun 27, 2019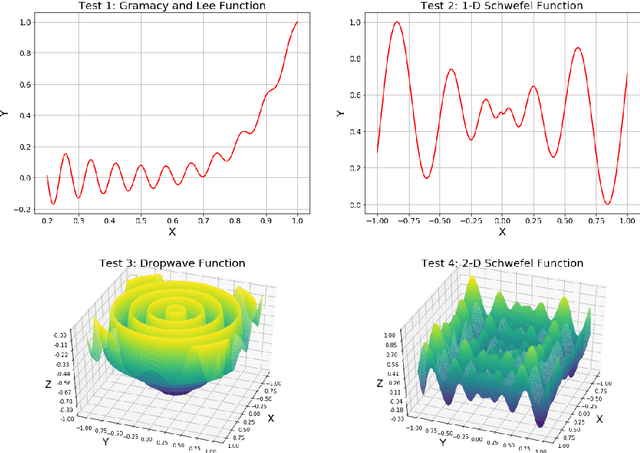

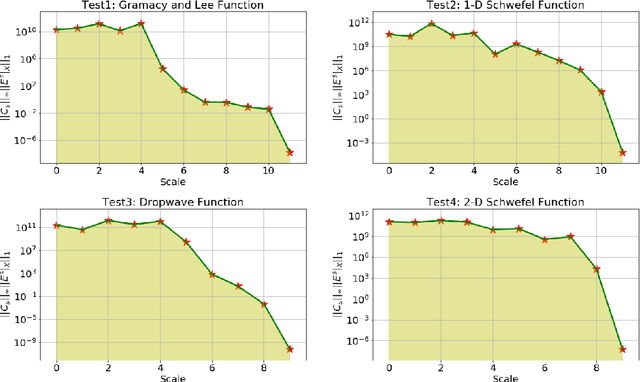
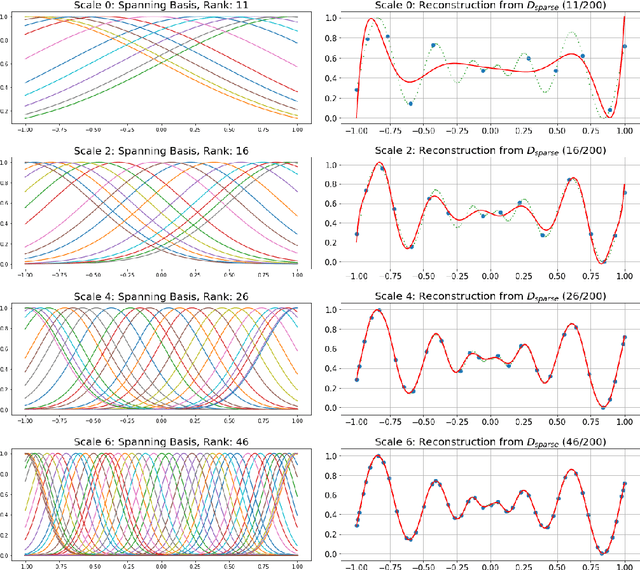
Paper proposes a hierarchical learning strategy for generation of sparse representations which capture the information content in large datasets and act as a model. The hierarchy arises from the approximation spaces considered at successively finer data dependent scales. Paper presents a detailed analysis of stability, convergence and behavior of error functionals associated with the approximations and well chosen set of applications. Results show the performance of the approach as a data reduction mechanism on both synthetic (univariate and multivariate) and real datasets (geo-spatial, computer vision and numerical model outcomes). The sparse model generated is shown to efficiently reconstruct data and minimize error in prediction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge